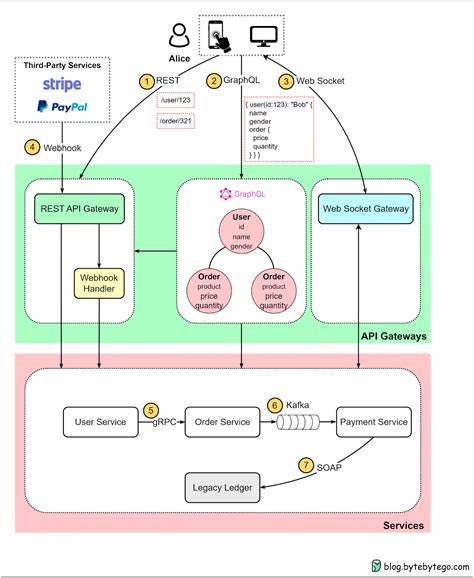
Die Gestaltung von APIs spielt eine entscheidende Rolle bei der Entwicklung moderner Softwarebibliotheken, insbesondere wenn es um komplexe Strukturen wie Maps geht. Die funktionalen Eigenschaften dieser Strukturen sind mehr als nur Programmierdetails – sie spiegeln tiefere mathematische und algebraische Prinzipien wider, die sich auf ihre Effektivität und Flexibilität auswirken. Ein besonders interessanter Blickwinkel ist dabei die Analyse von Maps über algebraische Gesetze, die erlaubt, besser zu verstehen, warum bestimmte Designentscheidungen getroffen werden und welche Konsequenzen sie für Benutzer und Entwickler haben. In der funktionalen Programmierung wird eine Map häufig als eine Funktion vom Typ k -> Maybe v betrachtet, die Schlüssel auf optionale Werte abbildet. Dieses Konzept führt dazu, das Fehlen eines Schlüssels durch das Nothing repräsentiert wird.
Bei der Praxis mit Haskell und der bekannten Bibliothek Data.Map sieht man, dass diese Abbildung sinnvoll ist, aber auch zu gewissen Zwängen führt – zum Beispiel bei der Definition der Funktion unionWith. Die Funktion unionWith aus Data.Map hat den Typ (a -> a -> a) -> Map k a -> Map k a -> Map k a und verbindet zwei Maps, wobei Werte mit gleichen Schlüsseln durch eine Funktion kombiniert werden. Eine berechtigte Frage ist, warum unionWith nicht unterschiedliche Werttypen unterstützt, wie es beispielsweise intersectionWith mit (a -> b -> c) erlaubt.
Ein möglicher Ansatz wäre eine Funktion unionWith, die als Parameter eine Funktion vom Typ Maybe a -> Maybe b -> c akzeptiert, um die unterschiedlich getypten Werte zu verarbeiten. Jedoch birgt diese Variante das Problem, dass sie theoretisch auch mit Nothing Nothing aufgerufen werden könnte, was semantisch nicht zur Idee einer Vereinigung passt. Als elegantere Alternative bieten sich algebraische Datentypen wie These a b an, die ausschließen, dass beide Werte gleichzeitig fehlen können. These definiert eine Werteoption, die genau einen Wert vom Typ a oder b oder beide enthält. So kann eine Funktion unionWith des Typs (These a b -> c) -> Map k a -> Map k b -> Map k c definiert werden, die logisch und sicherer vermittelt, wie Werte zusammengeführt werden.
Doch um wirklich zum Kern der Sache zu kommen, müssen wir die philosophische Frage stellen, was eigentlich eine Map ist. Hinter dieser Datenstruktur steckt weit mehr als nur eine zweckmäßige Key-Value-Zuordnung. Betrachtet man eine Map als eine effiziente Repräsentation der Funktion k -> Maybe v, so stellt sich die Frage, warum der Wert tatsächlich eine Maybe-Option ist. Der Einsatz von Maybe dient vor allem dazu, den Fall des Fehlens eines Schlüssels zu modellieren. Diese Interpretation kann jedoch erweitert und verallgemeinert werden, indem wir Maybe durch eine Monoid-Struktur ersetzen und die Map damit als k -> v mit Monoid v betrachten.
Ein Monoid ist eine algebraische Struktur, die einen neutralen Wert (mempty) und eine assoziative Binäroperation (<>) definiert. Diese Verallgemeinerung entfernt die Beschränkung, nur auf optionale Werte zuzugreifen, und erlaubt es, durch das Monoid repräsentierte „Standardwerte“ für jede mögliche Schlüsselabfrage zu definieren. Eine Map wird somit als Funktion verstanden, die für jeden Schlüssel einen Wert ausgibt, der mindestens den neutralen Wert hat, wenn kein expliziter Eintrag vorhanden ist. Diese Sichtweise ermöglicht ein elegantes Verständnis vom rechten Bias, der in Data.Map implementiert ist.
Unter der Maybe-Interpretation wirkt es schwer nachvollziehbar, dass lookup k (singleton k v1 <> singleton k v2) den Wert Just v2 zurückgibt, doch wenn man das Map als k -> v mit Monoid v interpretiert, wird die Gleichheit lookup k (m1 <> m2) = lookup k m1 <> lookup k m2 verständlich. Insbesondere wenn das Monoid speziell als Last-Monoid gewählt wird, erklärt sich das Verhalten als ein Semigroup-Homomorphismus. Mit diesem erweiterten Verständnis lässt sich die ursprüngliche Frage zur Funktion unionWith elegant erneut formulieren. Nun lautet der Typ: unionWith :: (a -> b -> c) -> Map k a -> Map k b -> Map k c Dank der Monoidstruktur verringert sich das Problem, was bei fehlenden Schlüsseln passieren soll. Statt mit Nothing müssen wir nur mit dem neutralen Wert mempty arbeiten.
Die Funktion unionWith wird also für alle Schlüssel den Wert f (lookup k m) (lookup k n) zurückgeben. Trotzdem gibt es Probleme bei der Implementierung und Effizienz. Betrachtet man den Fall, dass man eine Funktion f definiert, die unabhängig von den Eingabewerten einen bestimmten Wert nontrivial zurückgibt, so ergibt sich für alle Schlüssel k: lookup k (unionWith f m n) = nontrivial Um eine solche Map zu realisieren, muss man entweder jeden Schlüssel explizit mit nontrivial assoziieren – was ineffizient und speicherintensiv wäre – oder eine Möglichkeit finden, den Wert nontrivial als eine Art Defaultwert zu speichern, der bei jeder Lookup-Operation genutzt wird. Die zweite Option führt zu einer spannenden Konstruktion: Eine Map speichert nicht nur Daten in Form einer internen Baumstruktur (wie es bei Data.Map der Fall ist), sondern besitzt zusätzlich einen impliziten Default-Wert, der zurückgeliefert wird, wenn kein passender Eintrag gefunden wird.
Formal kann dies als ein zweigeteilter Datentyp definiert werden, der aus einem Default-Wert und der eigentlichen Implementierung (einem balancierten Suchbaum) besteht. Allerdings wirft diese Konstruktion komplexe Probleme auf, wenn man sie mit Semigroup-Homomorphismen in Einklang bringen will. Beispielsweise gilt für einen Monoid-Operator (<>) die Eigenschaft lookup k (m1 <> m2) = lookup k m1 <> lookup k m2 Spezialfall ist hier, wenn m2 als Map mit einem konstanten Standardwert nontrivial definiert wird. Dann müssen wir in jedem Lookup-Ergebnis die Operation mit nontrivial durchführen, um diese Eigenschaft zu gewährleisten. Die entscheidende Herausforderung liegt darin, diese Rechnung effizient zu gestalten.
Die Option, für jeden Schlüssel den Wert explizit zu modifizieren, ist bei großen Maps aufgrund der linearen Zeitkomplexität unpraktisch. Die andere Annahme ist, dass man Berechnungen verzögert oder suspendiert, bis ein Wert wirklich benötigt wird – aber eine Map in Form eines balancierten binären Suchbaums ist nicht dafür gebaut, solche komplexen „Lazy“-Kombinationen effizient abzubilden. Dieser Sachverhalt erklärt auch, warum typische Map-Implementierungen keine funktionale Applicative-Instanz haben. Obwohl man intuitiv denken könnte, dass ein solcher Applicative-Zugang durch Monoid-Beschränkungen eingeschränkt wird, ist die eigentliche Ursache die Unmöglichkeit, eine effiziente Implementierung mit den notwendigen algebraischen Eigenschaften bereitzustellen. Der spannende Punkt an dieser algebraischen Analyse ist, dass sie ohne einen Blick in den Quellcode von Data.
Map auskommt. Nur durch Annahmen über die algebraischen Gesetze, die APIs erfüllen sollten, und durch das Durchspielen extremer (degenerierter) Funktionsbeispiele lässt sich ein tiefgreifendes Verständnis für die Notwendigkeiten und Beschränkungen gewinnen. Die Verbindung zwischen theoretischer Algebra und praxisnaher API-Gestaltung führt so zu einem besseren Gespür für die Konstruktion flexibler und effizienter Datentypen. Dabei zeigt sich auch, dass subjektives Gefühl von „Reasonableness“ oder „Reasonableness out of the picture“ durch harte Gesetze ersetzt wird, die Designentscheidungen untermauern. Für Entwickler bedeutet das vor allem, dass manche Einschränkungen im Design nicht als Schwächen, sondern als bewusste Kompromisse verstanden werden sollten, um Performance und weiteres Verhalten optimal zu gestalten.
Die algebraische Sichtweise schärft das Bewusstsein für solche Kompromisse und fördert damit eine sachkundige Diskussion rund um API-Designs und ihre Implementierungen. Abschließend bleibt festzuhalten, dass algebraische Gesetze nicht nur theoretische Konzepte sind, die in abstrakten mathematischen Texten ihren Platz haben. Sie bieten praktische Werkzeuge, um Softwarestrukturen auf einer fundamentalen Ebene zu verstehen und zu optimieren. Durch die Anwendung dieser Prinzipien auf Maps und ihre Operationen erhalten wir wertvolle Erkenntnisse, warum so manche API-Signaturen so gewählt sind, wie sie gewählt wurden – und wohin sich zukünftiges Design und Implementierung weiterentwickeln kann.