Die Neurowissenschaft und Biologie sind seit Jahrzehnten durchdrungen von einem bestimmten Paradigma: der Annahme, dass neuronale Netzwerke und dynamische Systeme die zentralen Modelle sind, um biologische Prozesse und insbesondere die Informationsverarbeitung im Gehirn oder zelluläre Abläufe zu verstehen. Dieses Paradigma ist tief verwurzelt und hat viele bedeutende Erkenntnisse und Fortschritte hervorgebracht. Dennoch stellen einige Stimmen, wie die in Diskussionsforen und wissenschaftlichen Debatten, diese Auffassung infrage und fordern eine Erweiterung oder gar eine Neuorientierung in der Erforschung biologischer Systeme. Die Gedanken dahinter sind keineswegs nur akademisch, sondern berühren die grundlegende Frage, wie Leben wirklich Berechnung und Informationsverarbeitung realisiert. Diese Reflexion entführt uns in die Grenzen der traditionellen Modelle und eröffnet spannende neue Perspektiven.
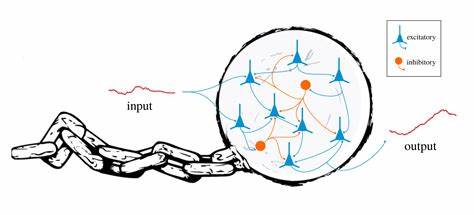
Die dominierende Hypothese vieler biologischer Modelle ist, dass biologische Prozesse auf Netzwerken basieren. Die Art und Weise, wie Neuronen Signale austauschen – durch Erregung oder Hemmung – bildet die Grundlage für viele kognitive Vorgänge. Gleichzeitig werden in der Entwicklungsbiologie genetische Netzwerke für die komplexen Prozesse der Zellteilung und Differenzierung verantwortlich gemacht. Die Vorstellung, dass eine endliche Anzahl von Variablen mit definierten Wechselwirkungen ausreicht, alle relevanten biologischen Phänomene zu erklären, ist weit verbreitet. Man verbindet diese Wechselwirkungen oft mit mathematischen Konzepten aus dynamischen Systemen, die sich durch Differentialgleichungen beschreiben lassen.
Auf den ersten Blick erscheint dieses Modell als überaus vielseitig und leistungsfähig. Auch komplexe Vorgänge wie dendritische Integration in einzelnen Neuronen können als Netzwerke von Signalpfaden modelliert werden, und selbst molekulare Prozesse wie Phosphorylierungen, die neuronale Aktivität modulieren, fügen sich in dieses Bild ein. Das Problem dabei ist jedoch, dass es sich bei diesen Modellen meist um Finite-Dimensionale dynamische Systeme handelt. Das bedeutet, dass das System zu jedem Zeitpunkt durch eine vorgegebene, endliche Anzahl von Variablen beschrieben wird, deren zeitliche Veränderung durch vordefinierte Gleichungen geregelt ist. Diese mathematische Formalisierung ist elegant, aber auch einschränkend.
Ein kritischer Einwand gegen dieses Paradigma ist, dass Finite-Dimensionale dynamische Systeme in ihrer Rechenkapazität begrenzt sind. Und hier kommen grundlegende theoretische Konzepte aus der Informatik ins Spiel. Die klassische Berechnungstheorie zeigt, dass Turingmaschinen einen entscheidenden Maßstab für universelle Berechenbarkeit darstellen. Turingmaschinen sind formale Modelle, die alles berechnen können, was im Prinzip berechenbar ist, vorausgesetzt, sie haben ausreichend Ressourcen wie Zeit und Speicher. Ein wesentliches Merkmal dieser Modelle ist, dass die Menge der benötigten Ressourcen nicht im Voraus festgelegt sein muss.
Sie können beispielsweise unbegrenzt viel Speicher anfordern, um komplizierte Aufgaben zu lösen. Dem gegenüber stehen dynamische Systeme, die von einer festen Anzahl an Variablen ausgehen und deren Zustand sich innerhalb eines vorgegebenen Zustandsraums bewegt. Weil sie keine echte Möglichkeit besitzen, ihre Dimensionen während der Berechnung zu erweitern, sind sie in ihren Rechenfähigkeiten beschränkt. Es ist auch nicht möglich, eine dynamische Systembeschreibung zu entwerfen, die für beliebig große Informationsmengen durch Umgestaltung erweitert werden kann. Zwar können neuronale Netzwerke und dynamische Systeme äußerst komplexe Muster erkennen und einfache Berechnungen durchführen, doch so beeindruckend ihre Leistungen beispielsweise in Anwendungen wie Deep Learning oder der Simulation biologischer Sensorik auch erscheinen mögen, bleiben sie hinter der universellen Berechenbarkeit zurück.
Wichtig ist zu verstehen, dass Turingmaschinen oder gleichwertige Modelle wie Programmiersprachen keine physikalischen Geräte im klassischen Sinn sind, sondern abstrakte Berechnungsmodelle. Die eigentliche Stärke liegt darin, dass Programme Speicher dynamisch anfordern und dadurch auf Probleme mit variabler und gegebenenfalls unvorhersehbarer Inputgröße reagieren können. Im Gegensatz dazu sind dynamische Systeme und neuronale Netzwerke, die von einer fixen Struktur ausgehen, niemals so flexibel. Diese Tatsache wirft Fragen darüber auf, ob die verbreiteten Modelle der Biologie ausreichend sind, um die wahre Rechenleistung lebender Organismen zu erfassen. Denn Zellen, Organe und ganze Organismen können wachsen, vielfältige Komponenten neu zusammensetzen und in gewissem Maße in ihrer Komplexität variieren.
Wenn man einen Organismus als eine Art Rechner betrachtet, dann sind seine Ressourcen nicht immer vorausbestimmt oder fixiert. Evolutionäre Prozesse können neue Strukturen schaffen, die als Erweiterungen oder Erweiterungen der ursprünglichen Rechnerarchitektur interpretiert werden können. Ein weiterer entscheidender Punkt ist die Frage nach der Realisierbarkeit universeller Berechnung auf biologischer Ebene. Einige Studien zeigen, dass unter idealisierten Bedingungen finite-dimensionale dynamische Systeme Turingmaschinen simulieren können. Diese Simulationen basieren jedoch auf unrealistischen Voraussetzungen, wie unendlich präziser Repräsentation von Zuständen – etwa einer Zahl, deren Dezimalstellen als eine unendliche Speicherband-Kette interpretiert wird.
Diese Annahmen sind in lebenden Systemen so nicht gegeben, physikalische Messgrößen und chemische Konzentrationen sind immer begrenzt und verrauscht. Diese mangelnde sogenannte „strukturelle Stabilität“ macht die Modelle für die Praxis fraglich. Somit wird die Schlussfolgerung laut einiger Theoretiker, dass bisherige Modelle aus Neurowissenschaft und Entwicklungsbiologie nicht mit der Komplexität und den Rechenfähigkeiten lebender Systeme Schritt halten können. Es wird vorgeschlagen, das Augenmerk stärker auf molekulare Ebenen zu richten, insbesondere auf Systeme basierend auf DNA und RNA. Diese Moleküle verfügen über Eigenschaften, die ihnen eine symbolhafte, codierte Informationsverarbeitung ermöglichen.
Die Sequenzen von Nukleotiden stellen Zeichenketten dar, deren Verarbeitung algorithmisch erweitert und angepasst werden kann, ähnlich wie es Programme in einem Computer tun. Ein radikales Gedankenexperiment in der theoretischen Biologie ist die Vorstellung, dass biologische Universalcomputer in der Molekularbiologie bereits existieren oder zumindest entstehen könnten. Dies würde bedeuten, dass lebende Systeme nicht allein durch fixe Netzwerke und dynamische Wechselwirkungen erklärbar sind, sondern vielmehr, dass sie eine universelle Berechnungstiefe erreichen – durch Mechanismen, die bisher nicht hinreichend verstanden oder entdeckt wurden. Beispielsweise könnten RNA-Editing-Prozesse dazu in der Lage sein, komplexe Algorithmen ablaufen zu lassen, die universelle Berechnung erlauben. Solche Systeme wären auch evolutionär sehr vorteilhaft, da sie enorme Flexibilität und Anpassungsfähigkeit ermöglichen.
Natürlich stößt diese Vorstellung in der traditionellen Biologie auf Skepsis. Die klassische Lehrmeinung sieht DNA und RNA vor allem als passive Informationsspeicher und Vermittler der Proteinbiosynthese, nicht als aktiven Computer. Dennoch häufen sich Indizien, die eine deutlich größere Rolle der Moleküle im biologischen Informationsmanagement nahelegen. Dies zeigt sich etwa in Untersuchungen zur Gedächtnisbildung, bei der molekulare Mechanismen eine tragende Rolle spielen könnten, oder in der Erforschung des nicht-protein-kodierenden Genoms, das als ein bisher zu wenig beachtetes Reservoir funktioneller Information gilt. Was bedeutet das für zukünftige Forschungen? Wissenschaftler sind gefordert, über die Grenzen etablierter Paradigmen zu blicken und neue Modelle zu entwickeln, die biologische Universalcomputer realistisch abbilden.
Dabei gilt es, experimentelle Evidenz sorgfältig zu prüfen, neuronale Netzwerke mit ihren dynamischen Eigenschaften zu hinterfragen und den molekularen, zellulären und genetischen Ebenen mehr Raum in der Untersuchung einzuräumen. Es ist nötig, interdisziplinäre Ansätze zu verfolgen, die Biologie, Physik, Informatik und Philosophie auf neue Weise verbinden. Letztlich ist die zentrale Herausforderung, zu verstehen, wie lebende Systeme die komplexen Berechnungen durchführen, die nötig sind für Wahrnehmung, Anpassung, Lernen und Entwicklung. Wir müssen die Rolle von Wachstum, Speichererweiterung und nichtlinearen dynamischen Prozessen besser begreifen. Vielleicht liegt die Antwort nicht allein in Netzwerken von Neuronen oder Genen, sondern in einer Hybridform oder völlig neuen Computationsformen, die erst noch zu entdecken sind.
So wie Computertechnologie Fortschritte brachte, indem sie von eingeschränkten Schaltkreisen zu universeller Berechenbarkeit wuchs, könnte die biologische Forschung kurz vor einem Paradigmenwechsel stehen, in dem die wahre Natur biologischer Informationsverarbeitung und Berechnung erkannt wird. Eine solche Erkenntnis hätte weitreichende Konsequenzen – für Medizin, Künstliche Intelligenz, Robotik und unser grundlegendes Verständnis von Leben selbst. Es lohnt sich deshalb, das starre Festhalten an traditionellen Netzwerkkonzepten zu überdenken und offen für neue, tiefgreifende Ansätze zu sein, die der Komplexität und Vielfalt des Lebens gerecht werden.