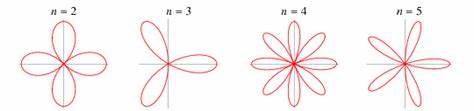
Rosen sind seit Jahrhunderten ein Symbol für Schönheit und Liebe, und ihre Blütenblätter sind ein wesentlicher Bestandteil ihres unverwechselbaren Charmes. Doch hinter der scheinbar einfachen Eleganz der Rosenblätter verbirgt sich eine faszinierende mathematische und physikalische Komplexität, die lange Zeit unerforscht blieb. Moderne Forschungsergebnisse kombinieren theoretische Mathematik, physikalische Experimente und Computersimulationen, um zu erklären, wie die Form der Rosenblätter entsteht und warum gerade die charakteristischen Spitzen an ihren Rändern erscheinen. Die Entschlüsselung dieses natürlichen Musters eröffnet nicht nur neue Erkenntnisse in der Pflanzenbiologie, sondern auch in Bereichen wie Materialwissenschaften und moderner Biohinspired-Design-Technologie. In den vergangenen Jahren hat sich ein interdisziplinäres Forscherteam mit der Aufgabe beschäftigt, das Wachstum von Rosenblättern auf mikroskopischer Ebene zu verstehen.
Dabei zeigte sich, dass das Wachstum der Blätter keine gleichmäßige oder zufällige Expansion ist, sondern dass es von einem ungewöhnlichen geometrischen Feedback-Mechanismus gesteuert wird. Diese Art von Rückkopplung war in der Natur bisher nicht bekannt und ermöglicht es den Rosenblättern, ihre charakteristischen, sich nach außen rollenden Ränder und die spitzen Enden auszubilden. Die Grundlage dieses Mechanismus liegt in der Art, wie die Zellstruktur der Blätter mechanischen Druck und Zugkräften ausgesetzt ist und darauf reagiert. Während das Blatt wächst, werden interne Spannungen aufgebaut, die das Material dazu bringen, sich auf bestimmte Weisen zu verbiegen und zu formen. Physikalische Modelle zeigen, dass diese mechanische Rückkopplung das Wachstum nicht nur steuert, sondern auch stabilisiert, wodurch die spezifische, ästhetisch ansprechende Form der Rosenblätter entsteht.
Ein weiterer spannender Aspekt der Forschung beinhaltet die Simulation des Wachstumsprozesses mit flexiblen, dehnbaren Kunststofffolien, die den Eigenschaften von Pflanzengewebe ähneln. Diese Experimente erlaubten es den Wissenschaftlern, das Verhalten der Materialien unter kontrollierten Bedingungen zu beobachten und die Theorie des geometrischen Feedbacks zu bestätigen. Dabei erwies sich, dass die Kantenneigung und die Spitzenbildung am Rand der Blätter auf diese mechanischen Reaktionen zurückzuführen sind, wobei das Material versucht, die innere Spannung durch eine Art natürlicher Formgebung zu lösen. Mathematisch betrachtet spielen nichtlineare Differentialgleichungen und Konzepte aus der Geometrie und Topologie eine wichtige Rolle. Die Beschreibungen des Wachstumsprozesses sind komplex, da das Blatt nicht nur in zwei Dimensionen expandiert, sondern die Formierung in einem dreidimensionalen Raum stattfindet.
Die Querverbindung zwischen Wachstumskraft, Gewebeelastizität und Formänderung führt zu einer dynamischen und spezifischen Morphogenese der Rosenblätter. Solche mathematischen Modelle sind auch für andere Pflanzenarten von Interesse, da sie helfen können, Wachstumsprozesse zu verstehen, die für die Landwirtschaft und Botanik relevant sind. Der Entdeckung dieser ungewöhnlichen mathematischen Prinzipien liegen auch praktische Anwendungen zugrunde. So können Forscher durch die Nachahmung dieser natürlichen Rückkopplungsmechanismen neue, flexible Materialien und Strukturen entwickeln, die sich bei Belastung selbst anpassen, ähnlich wie die Rosenblätter. Diese biomimetische Herangehensweise ist vielversprechend für innovative Designs in Bereichen wie Architektur, Robotik und medizinischen Implantaten.
Zusätzlich bietet das Verständnis dieses Wachstumsmechanismus neue Einblicke in Entwicklungsbiologie und Biophysik, insbesondere wie Pflanzen ihre Form und Funktion optimieren. Die Spitzenbildung an den Rosenblättern könnte evolutionäre Vorteile bieten, beispielsweise in der Regenwasserableitung oder im Schutz vor Fressfeinden. Insgesamt zeigt diese Forschung, wie eng Natur und Mathematik miteinander verwobenen sind und wie komplexe natürliche Strukturen wie Rosenblätter durch zugrunde liegende physikalische Gesetze und mathematische Prinzipien entstehen. Die Entdeckung des geometrischen Feedbacks in Rosenblättern öffnet neue Perspektiven für weiterführende Studien in verschiedenen Wissenschaftsdisziplinen und verdeutlicht die Bedeutung von interdisziplinären Ansätzen bei der Lösung biologischer Rätsel. Im Kern bietet die ungewöhnliche Mathematik, die das Wachstum der Rosenblätter bestimmt, einen faszinierenden Blick in die Schönheit der Natur und die verborgenen Regeln, die ihre Formen prägen.
Von der Analyse der inneren Spannungen bis hin zur komplexen Modellierung des Wachstumsprozesses setzt dieses Wissen neue Maßstäbe für unser Verständnis von Pflanzenwachstum und ästhetischer Naturformung. Damit liegt ein Schlüssel vor, der in Zukunft nicht nur die Wissenschaft, sondern auch die Technik und das Design nachhaltig beeinflussen kann.