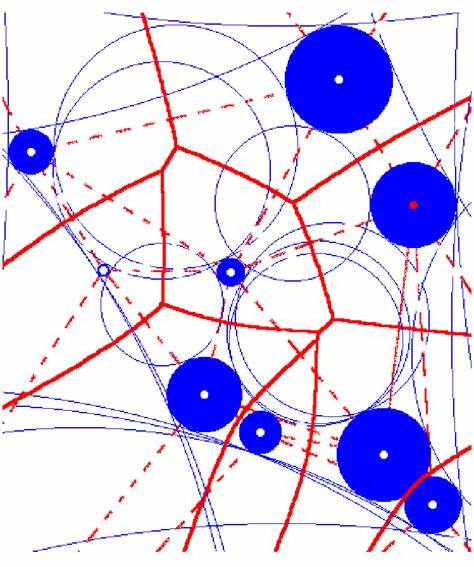
Die Voronoi-Diagramme sind ein zentrales Konzept in der Geometrie und Computergrafik, das zahlreiche Anwendungen von Standortplanung über Robotik bis hin zur medizinischen Bildverarbeitung ermöglicht. Eine besonders interessante Variante dieses Diagrammtyps ist das additiv gewichtete Voronoi-Diagramm. Es erweitert die klassischen Voronoi-Strukturen durch die Einbeziehung von Gewichten, die die Entfernungen zwischen beliebigen Punkten in der Ebene modifizieren. Dieses Konzept führt zu einer faszinierenden Struktur, bekannt auch als hyperbolische Dirichlet-Tessellation, deren Kanten sich aus hyperbolischen Bögen und geraden Linien zusammensetzen. Im Gegensatz zu den ungewichteten Voronoi-Diagrammen, bei denen jeder Punkt in einer Ebene dem nächstgelegenen sogenannten Generator zugeordnet wird, verändern bei additiv gewichteten Voronoi-Diagrammen die Gewichte die Zuordnung.
Man kann sich diese Gewichte vorstellen wie Wertminderungen, die von der Distanz subtrahiert werden. Konkret bedeutet das, an jedem Stützpunkt wird eine bestimmte positive Zahl zugewiesen, die von der normalen euklidischen Entfernung abgezogen wird, bevor die Zugehörigkeit bestimmt wird. Die dadurch entstehenden Zellen sind nicht mehr unbedingt konvex oder zusammenhängend, sondern können durch ihre neue Geometrie oft komplexere Formen annehmen. Aus mathematischer Sicht ergibt das additiv gewichtete Voronoi-Diagramm eine neue Art der Partitionierung eines Raumes, die besonders in der Theorie der hyperbolischen Geometrie relevant ist. Die Kanten der Zellen, welche die Grenzen zwischen einzelnen Regionen bilden, verlaufen nicht immer als gerade Linien, sondern häufig als hyperbolische Kurven.
Diese Eigenschaft hat der hyperbolischen Dirichlet-Tessellation ihren Namen gegeben und bringt neue Herausforderungen aber auch Chancen für die analytische Behandlung dieser Strukturen mit sich. Ein grundlegender Anwendungsbereich der additiv gewichteten Voronoi-Diagramme liegt in der Standortanalyse und Optimierung. Dort kann die Wahl von Gewichtungen die Reichweite und Anziehungskraft bestimmter Standorte modellieren, sodass ein realistischeres Bild von Einzugsgebieten entsteht als bei der rein geometrischen Bestimmung. In der Telekommunikation etwa hilft das Gewicht, die Signalstärke oder Kapazitäten unterschiedlicher Basisstationen zu repräsentieren. Daraus resultieren Einflüsse auf die dynamische Netzplanung und Optimierungsalgorithmen.
Auch in der Robotik und im autonomen Fahren finden diese Diagramme Anwendung. Das Planen von Bewegungsbahnen oder das Abstecken von Überwachungszonen kann durch die Berücksichtigung unterschiedlicher Gewichtungen für Sensoren oder Aktuatoren effektiver gestaltet werden. Die hyperbolische Natur der Kanten zwingt dabei dazu, neben den geradlinigen Wegen auch gebogene Pfade im Raum zu analysieren, was eine präzisere Navigation ermöglicht. Die Erstellung und Berechnung solcher additiv gewichteten Voronoi-Diagramme stellt eine mathematisch und algorithmisch anspruchsvolle Aufgabe dar. Während konventionelle Voronoi-Diagramme auf bekannten und gut optimierten Algorithmen beruhen, erfordern die neuen Kantenformen und die Anpassung an Gewichtungen spezialisierte Verfahren.
Es existieren verschiedene Ansätze, die von direkten Berechnungen aus der Definition über Nutzung von geometrischen Dualitäten bis zu iterativen numerischen Methoden reichen. Softwarebibliotheken und wissenschaftliche Implementierungen stellen teilweise Quellcode bereit, um Forschern und Entwicklern den Einstieg zu erleichtern. Die theoretischen Grundlagen dieser Konstruktionen sind eng mit der Theorie der hyperbolischen Geometrie verbunden. Anders als in der euklidischen Ebene führt die Subtraktion der Gewichte zu verzerrten Abständen, die einer Messung in einem Raum mit negativer Krümmung ähneln. Dies öffnet Türen für die Verknüpfung des Problems mit Disziplinen wie Differentialgeometrie und algebraischer Topologie und lädt zu interdisziplinären Forschungsansätzen ein.
Trotz der Komplexität werden additiv gewichtete Voronoi-Diagramme in praktischen Anwendungen zunehmend wichtiger. Auch im Bereich der computergestützten Bildverarbeitung ermöglichen sie präzisere Segmentierungen, zum Beispiel wenn unterschiedliche Pixel oder Markierungen unterschiedliche Wichtigkeit besitzen. Dies verbessert Detektions- und Klassifikationsverfahren erheblich. Das Verständnis der Struktur dieser Diagramme sowie ihrer Algorithmen unterstützt nicht nur die wissenschaftliche Arbeit, sondern fördert auch Innovationen in diversen Industriezweigen, die von Geoinformationssystemen über die Netzwerktechnik bis zur künstlichen Intelligenz reichen. Die Fähigkeit, Räume unter berücksichtigtem Gewichtungsfaktor sinnvoll zu unterteilen, erhöht die Genauigkeit von Modellen und die Effizienz in der praktischen Umsetzung.
Zusammenfassend lässt sich sagen, dass additiv gewichtete Voronoi-Diagramme als verallgemeinerte Form der klassischen Voronoi-Partitionen ein faszinierendes Forschungsfeld darstellen, das auf komplexen mathematischen Konzepten beruht und gleichzeitig weitreichende praktische Anwendungsfelder erschließt. Durch ihre charakteristische Geometrie und die damit verbundenen hyperbolischen Eigenschaften bieten sie neue Perspektiven für die Analyse von räumlichen Verteilungen und das Design smarter Systeme. Für alle, die sich näher mit dem Thema beschäftigen möchten, stehen diverse wissenschaftliche Publikationen sowie Open-Source-Quellcodes bereit, die das Studium und die Implementierung erleichtern. Sei es zur Vertiefung theoretischer Fragestellungen oder zur praktischen Entwicklung – additiv gewichtete Voronoi-Diagramme bergen ein großes Potenzial zur Innovation und zur Erweiterung des Verständnisses komplexer räumlicher Strukturen.