Das französische Tilgungssystem, auch als Annuitätentilgung bekannt, ist eine der gängigsten Methoden zur Rückzahlung von Hypothekendarlehen. Viele Menschen haben beim Abschluss einer Baufinanzierung oder eines Immobiliendarlehens bereits davon gehört, verstehen jedoch nicht im Detail, wie es funktioniert und warum die monatlichen Zahlungen stets gleich bleiben, während sich der Anteil von Zins und Tilgung im Verlauf der Zeit verschiebt. Dieses System zeichnet sich durch eine konstante monatliche Belastung aus, die sich aus einem Zins- und einem Tilgungsanteil zusammensetzt. Im Verlauf der Laufzeit verringert sich der Zinsanteil kontinuierlich, während die tatsächliche Rückzahlung des Darlehens, der Tilgungsanteil, immer größer wird. Dabei ist das Verständnis dieses Prinzips sowohl für Kreditnehmer als auch für jene von Bedeutung, die sich mit Finanzplanung und Immobilienfinanzierung auseinandersetzen möchten.
Beim Abschluss eines Darlehens mit festem Zinssatz wird eine monatliche Rate festgelegt, die über die gesamte Laufzeit konstant bleibt. Diese Rate basiert auf drei wichtigen Faktoren: der Darlehenshöhe, dem vereinbarten Zinssatz und der Laufzeit beziehungsweise der Anzahl der Raten. Mit diesen drei Variablen lässt sich die monatliche Rate exakt berechnen, denn sie stellt die Summe aus Zinsen und Tilgung dar. Die zugrunde liegende Mathematische Formel für die Berechnung der monatlichen Rate, auch bekannt als Annuität, lautet: PMT = P × r × (1 + r)^n / ((1 + r)^n − 1). Hierbei steht PMT für die monatliche Zahlung, P für den Darlehensbetrag (Principal), r für den monatlichen Zinssatz und n für die Gesamtanzahl der Zahlungen.
Die Anwendung dieser Formel führt dazu, dass der Kreditnehmer vom ersten Monat an genau weiß, wie hoch seine monatliche Belastung sein wird und welcher Teil davon in den Zins und welcher in die Tilgung fließt. Zur Veranschaulichung ein Beispiel: Nehmen wir an, jemand möchte ein Darlehen über 100.000 Euro aufnehmen, mit einem festen Jahreszins von 3,5 Prozent. Dieses Darlehen soll in 25 Jahren vollständig zurückgezahlt werden. Befasst man sich mit den Details, wird zunächst der monatliche Zinssatz berechnet, indem der Jahreszins durch 12 geteilt wird, also 0,035 geteilt durch 12, was ungefähr 0,00292 oder 0,292 Prozent entspricht.
Die Laufzeit von 25 Jahren entspricht 300 Monaten. Setzt man diese Werte in die Formel ein, erhält man eine monatliche feste Rate von circa 500,84 Euro. Zunächst scheint das einfach, doch was passiert genau bei jeder einzelnen Zahlung? Wie setzen sich die 500,84 Euro aus Zins und Tilgung zusammen? Im ersten Monat werden Zinsen auf den gesamten Darlehensbetrag berechnet, also 100.000 Euro multipliziert mit 0,00292, was 292 Euro ergeben würde. Diese 292 Euro werden an den Kreditgeber als Zins gezahlt.
Der Rest der Rate, also 500,84 Euro minus 292 Euro, etwa 208,84 Euro, reduziert die eigentliche Darlehensschuld. Im zweiten Monat wird der Zins nun nicht mehr auf 100.000 Euro, sondern auf den neuen Darlehensbetrag von 99.791,16 Euro berechnet. So ergibt sich ein leicht geringerer Zinsbetrag von circa 291,39 Euro.
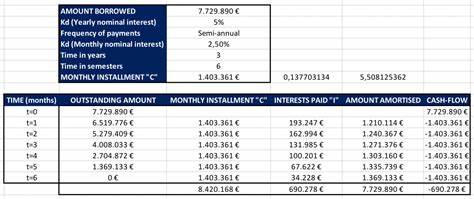
Damit steigt der Tilgungsanteil auf 500,84 Euro minus 291,39 Euro, was 209,45 Euro entspricht. Der Zinsanteil sinkt also, während der Tilgungsanteil wächst, obwohl die monatliche Gesamtzahlung unverändert bleibt. Dies ist der Kern der Annuitätentilgung: Die monatliche Belastung bleibt gleich, die Zusammensetzung verschiebt sich zugunsten der Tilgung. Im Laufe der Zeit bringt dieser Mechanismus den Kreditnehmer seiner vollständigen Rückzahlung näher. Eine Tabelle verdeutlicht die Entwicklung der Rate und ihrer Zusammensetzung Monat für Monat.
Anfangs dominiert der Zinsanteil, doch mit jeder weiteren Zahlung wächst der Betrag, der tatsächlich zur Tilgung des Darlehens verwendet wird. Am Ende der Laufzeit ist der Darlehensbetrag vollständig getilgt. Die mathematischen Grundlagen hinter diesem System basieren nicht allein auf einfacher Arithmetik, sondern auch auf Finanzmathematik und dem Konzept der Barwertberechnung. Die Festsetzung der Rate beruht auf der Berechnung des Barwerts eines Annuitätenstroms. Dabei wird der Wert aller zukünftigen Zahlungen diskontiert auf den heutigen Wert ermittelt, sodass die Summe anfänglich dem Kreditbetrag entspricht.
Der Bank oder dem Kreditgeber kommt dies zugute, indem sie sicherstellen, dass sie über die Laufzeit den vollen Darlehensbetrag zuzüglich Zinsen zurückerhalten. Das französische Tilgungssystem ist somit eine Anwendung der sogenannten Discounted-Cashflow-Methode, die finanzielle Ströme über Zeit bewertet. Für den Darlehensnehmer bedeutet dies Planbarkeit und Sicherheit durch konstante monatliche Belastungen. Für Finanzexperten ist es ein praktisches und bewährtes Modell, das Liquidität sowie Zins- und Tilgungsabfluss über die Kreditlaufzeit optimiert. Mit der Automatisierung durch Software und Programmiersprachen wie Python lassen sich Tilgungspläne schnell berechnen und visualisieren.
Beispielhaft kann hierfür ein kurzer Python-Code verwendet werden, der den Tilgungsplan erstellt, monatliche Zahlungen, Zins- und Tilgungsanteile auflistet sowie die Restschuld nach jeder Rate ermittelt. Für Kreditnehmer, Berater und Immobilienkäufer bietet dies eine wertvolle Hilfestellung zur Einschätzung der realen Belastung und zur besseren Finanzplanung. Neben der praktischen Anwendung in der Darlehensverwaltung gibt es auch spezialisierte Bibliotheken wie numpy-financial, die Funktionen zur Berechnung der regelmäßigen Zahlungen (pmt) oder der Zinsen für einzelne Abrechnungszeiträume (ipmt) bereitstellen. Solche Tools erleichtern Finanzanalysen und tragen zur Transparenz bei. Ein weiterer interessanter Aspekt dieses Systems ist der Einfluss auf die Gesamtkosten des Kredits.
Aufgrund der konstanten Raten zahlen Kreditnehmer am Anfang vorwiegend Zinsen, was bedeutet, dass dessen Zinslast zu Beginn höher ist. Dementsprechend sinkt die Zinsbelastung erst mit fortschreitender Laufzeit, während der Tilgungsanteil steigt. Das ist insbesondere bei langfristigen Darlehen wichtig zu beachten, wenn man beispielsweise zusätzliche Sondertilgungen plant oder vorzeitige Rückzahlungen erwägt. Durch das Verständnis der Zusammensetzung der Annuitäten besteht die Möglichkeit, den Tilgungsplan gezielt zu beeinflussen und Zinskosten langfristig zu reduzieren. Abgesehen von der einfacheren Handhabung für Kreditnehmer führt das französische Tilgungssystem auch zu einer gewissen Flexibilität in der Vertragsgestaltung.
Die Festlegung der Laufzeit und des Zinssatzes bestimmt die Höhe der monatlichen Zahlungen, sodass Darlehensnehmer entsprechend ihrer finanziellen Möglichkeiten eine passende Kombination wählen können. Da die Zahlungen konstant bleiben, erleichtert es auch die Haushaltsplanung und verhindert unerwartete Belastungsspitzen. Zusammenfassend ist das französische Tilgungssystem mehr als nur eine Standardmethode zur Rückzahlung von Krediten. Es veranschaulicht komplexe finanzmathematische Zusammenhänge, die in der täglichen Praxis von Immobilienfinanzierungen und Darlehensverträgen Anwendung finden. Für den Darlehensnehmer bedeutet es Klarheit, Planungssicherheit und den stetigen Aufbau von Eigenkapital in der Immobilie.
Für Banken und Kreditgeber stellt es eine bewährte Methode dar, um das Ausfallrisiko zu minimieren und den Rückfluss des Kapitals in planbaren Schritten sicherzustellen. Wer sich intensiv mit dem Thema Baufinanzierung auseinandersetzt, sollte die Funktionsweise der französischen Annuitätentilgung genau kennen. So lässt sich die Finanzierung nicht nur besser verstehen, sondern auch aktiv steuern. Die Fähigkeit, die monatlichen Zahlungen sinnvoll zu analysieren und deren Zusammensetzung zu interpretieren, ist ein wichtiger Schritt auf dem Weg zu einer erfolgreichen und nachhaltigen Immobilienfinanzierung. Mit Blick auf den finanziellen Erfolg und eine solide Vermögensbildung empfiehlt es sich, vor Abschluss eines Darlehens die Tilgungsmodalitäten genau zu prüfen und gegebenenfalls auch mit Fachleuten zu besprechen.
Die französische Annuitätentilgung bleibt dabei ein essenzielles Modell im Bereich der privaten sowie gewerblichen Kreditvergabe und bietet durch ihre mathematisch fundierte Struktur ein hohes Maß an Transparenz und Stabilität.