Titel: Gesetze, Potenzgesetze und Statistiken: Die unsichtbaren Kräfte der Datenanalyse In einer Welt, die zunehmend von Daten bestimmt wird, ist das Verständnis von Gesetzen, insbesondere von Potenzgesetzen, und deren Beziehung zur Statistik zu einer Schlüsselkompetenz geworden. Diese Prinzipien bilden das Rückgrat wissenschaftlicher Erkenntnisse und technologische Innovationen, und ihre Bedeutung reicht weit über die Grenzen der Physik hinaus. In diesem Artikel werden wir die Essenz dieser Konzepte ergründen und deren Implikationen aufzeigen. Gesetze in der Wissenschaft stehen für die grundlegenden Prinzipien, die das Verhalten von Naturphänomenen beschreiben. Sie ermöglichen es Wissenschaftlern, Vorhersagen zu treffen und Hypothesen zu überprüfen.
Doch nicht alle Gesetze sind gleich. Während einige, wie das Gesetz von Newton, relativ einfach und intuitiv sind, gibt es komplexere Phänomene, die oft durch Potenzgesetze dargestellt werden. Potenzgesetze haben eine besondere Faszination. Sie beschreiben Beziehungen zwischen zwei Variablen, bei denen eine der Variablen in Form einer Potenz der anderen ist. Ein klassisches Beispiel stammt aus der Geophysik: das Gutenberg-Richter-Gesetz, das die Beziehung zwischen der Größe von Erdbeben und deren Häufigkeit beschreibt.
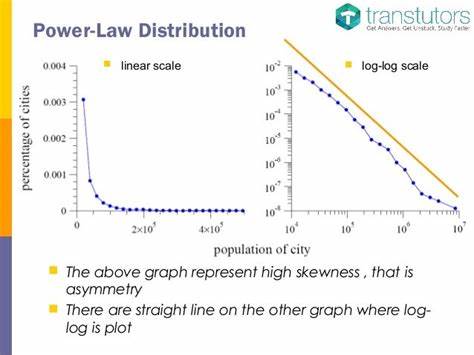
Gemäß diesem Gesetz sinkt die Wahrscheinlichkeit der Auftretens von Erdbeben mit zunehmender Energie des Erdbebens – mathematisch als 1/E^2 ausgedrückt. Dies weist darauf hin, dass es bei Erdbeben keinen inhärenten Maßstab gibt und dass sie über viele Größenordnungen hinweg verteilt sind. Doch woher stammt die Popularität dieser Potenzgesetze? Ein Grund liegt in der scheinbaren Einfachheit und Eleganz ihrer Darstellung. Wissenschaftler haben beobachtet, dass viele Phänomene – von der Häufigkeit von Wortnutzungen in einer Sprache bis hin zur Verteilung von Stadtgrößen – Potenzgesetze zu folgen scheinen. Diese universelle Anwendbarkeit hat das Konzept in verschiedenen Disziplinen salonfähig gemacht, sei es in der Physik, Biologie, Soziologie oder Wirtschaftswissenschaften.
Gleichzeitig bringt die Analyse dieser Gesetze auch Herausforderungen mit sich. Die Interpretation von Daten ist oft eine delikate Angelegenheit. Zahlreiche Studien, die behaupten, Potenzgesetze zu unterstützen, mussten im Lichte neuer Methodologien und statistischer Techniken überdacht werden. Ein Beispiel dafür ist die Arbeit von Aaron Clauset und seinen Kollegen, die gezeigt haben, dass die gängige Methode der linearen Regression in log-log-Diagrammen nicht immer die richtigen Schlussfolgerungen zulässt. Trotz der intuitive Anziehungskraft, die solche Diagramme bieten, liegen viele der angenommenen Beziehungen auf wackeligen statistischen Grundlagen.
Ein standhaftes Beispiel für die Herausforderungen bei der Analyse ist die Verteilung von Reichtum. Während häufig angenommen wird, dass die Reichtumsverteilung den Gesetzen der Potenz folgt, zeigen die Ergebnisse von Clauset et al., dass diese Hypothese nicht immer haltbar ist. In vielen Fällen ist die Verteilung besser durch exponentielle oder andere mathematisch fundierte Modelle zu erklären. Dies zwingt uns, unsere Wahrnehmung von Daten und deren Bedeutung zu hinterfragen.
Statistik ist nicht nur ein Werkzeug zur Datenanalyse; sie ist ein Filter, durch den wir die Welt wahrnehmen. Wenn wir uns mit Daten auseinandersetzen, stehen wir immer vor der Herausforderung, zwischen legitimen Beobachtungen und den Illusionen zu unterscheiden, die unser Verstand erzeugt. Es ist einfach, eine Hypothese aufzustellen und diese mit umfangreichen Daten zu untermauern, aber die eigentliche Herausforderung besteht darin, sicherzustellen, dass die gewählten Methoden auch tatsächlich das abbilden, was sie zu messen vorgeben. Ein eindrucksvolles Beispiel für die Anwendung von Potenzgesetzen ist das Internet. Die Verteilung der Anzahl von Verlinkungen auf Webseiten folgt oftmals einem Potenzgesetz.
Das bedeutet, dass einige Webseiten extrem viele Links erhalten, während die Mehrheit nur über wenige Links verfügt. Diese „Schwarmintelligenz“ spiegelt sich nicht nur in der digitalen Welt wider, sondern hat auch weitreichende gesellschaftliche und ökonomische Konsequenzen. Darüber hinaus betreffen Potenzgesetze auch natürlich vorkommende Phänomene wie Waldbrände oder den Erfolg von Unternehmen. Studien haben gezeigt, dass die Größe von Waldbränden ebenfalls durch ein Potenzgesetz beschrieben werden kann, das die Häufigkeit großer Brände im Vergleich zu kleineren regulären Bränden behandelt. Diese Erkenntnis hat Einfluss auf die Art und Weise, wie wir Naturkatastrophen verstehen und wie Ressourcen für Prävention und Reaktion eingeplant werden.
Der Umgang mit Daten ist in der modernen Welt unerlässlich. Die Fähigkeit, Daten sinnvoll zu analysieren, Zerfällung zu betreiben und Vorurteile zu erkennen, ist entscheidend für die Validierung wissenschaftlicher Hypothesen. Es ist jedoch wichtig zu betonen, dass Daten allein nicht das Endziel sind. Vielmehr sind es die Interpretationen und die Geschichten, die wir aus den Daten ableiten, die ihre wahre Bedeutung verleihen. In einer Zeit, in der sogenannte „Fake News“ und Fehlinformationen überhandnehmen, wird der kritische Umgang mit Daten und Statistiken relevanter denn je.