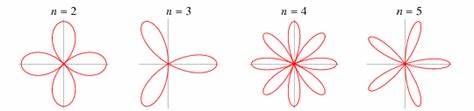
Rosen gelten seit jeher als Symbol für Schönheit, Liebe und Anmut. Ihre eleganten Blütenblätter, die sich oft mit feinen Spitzen und aufgerollten Rändern präsentieren, sind nicht nur ästhetisch beeindruckend, sondern auch ein wunderbares Beispiel für komplexe naturgegebene Formen. Für lange Zeit blieben die genauen Mechanismen, die diese einzigartige Form schaffen, ein Rätsel. Doch neue Forschungsergebnisse zeigen, dass hinter der Form von Rosenblättern eine erstaunliche und bisher in der Natur nicht beobachtete mathematische Dynamik steckt. Die Ausgangsbasis für das Verständnis der Blütenblattform liegt im Wachstum der Pflanze.
Während des Wachstums reagieren pflanzliche Zellen auf verschiedene chemische Signale, die ihr Zellwachstum steuern und koordinieren. Doch darüber hinaus wirkt nach neuester Erkenntnis auch eine mechanische Rückkopplung, die das Wachstum gezielt steuert und die Form präzise formen lässt. Insbesondere bei Rosenblättern wurde entdeckt, dass ihre nach außen aufgerollten Spitzen und die charakteristischen gerollten Kanten das Ergebnis eines ungewöhnlichen geometrischen Prinzips sind. Wissenschaftler nutzen eine Kombination aus theoretischer Mathematik, Computersimulationen und praktischen Experimenten, um diesen Effekt zu erforschen. Ein zentraler Anteil an der Arbeit waren Modelle mit dehnbaren Materialien ähnlich dem Gewebe von Rosenblättern, um das Wachstum und die dadurch entstehenden Formveränderungen zu analysieren.
Dabei zeigte sich, dass mechanische Spannungen im Gewebe nicht nur Resultate des Wachstumsvorgangs sind, sondern aktiv auf diesen zurückwirken – also eine Feedback-Schleife bilden. Diese Rückkopplung sorgt dafür, dass sich die Ränder der Blätter aufrollen und spitzenartige Formen entwickeln, die zuvor in der Natur nie so genau identifiziert und mathematisch beschrieben wurden. Das Wachstum ist somit nicht nur biochemisch, sondern auch mechanisch geregelt, was zu den ungewöhnlichen Formen führt. Diese Erkenntnis ist ein großer Durchbruch in der Entwicklungsbiologie und Biophysik, da sie zeigt, wie komplexe Naturformen durch ein inneres Zusammenspiel von Geometrie und Mechanik entstehen. Die Rolle der Mathematik ist hierbei besonders spannend.
Es handelt sich um eine Art nichtlineare Geometrie, bei der die Krümmung des Gewebes und die Spannungskräfte jeweils Einfluss aufeinander ausüben. Die Mathematiker sprechen von einem Feedback-System in der Geometrie, das Wachstum und Formgebung simultan steuert. Dieses Prinzip wurde bisher weder in der Pflanzenforschung noch anderswo in der Natur so detailliert beobachtet. Die Forscher um David Castelvecchi und Kollegen haben diese Methodik in der Zeitschrift Nature vorgestellt. Durch ihre Arbeit konnten sie nicht nur die Spitzen und gerollten Ränder der Rosenblätter reproduzieren, sondern auch allgemeingültige Schlüsse für das Wachstum von weichen, dünnen Materialien ziehen.
Die Anwendung ihrer Erkenntnisse kann weit über die Botanik hinausgehen, etwa in der Materialwissenschaft, wo flexible und formbare Werkstoffe zunehmend gefragt sind. Darüber hinaus trägt das Verständnis dieser Wachstumsmechanik zur weiterführenden Erforschung von biologischen Formen bei. Pflanzen, Tiere und sogar menschliche Organe weisen oft komplexe Strukturen auf, die nicht allein durch genetische Programme erklärt werden können. Die Beobachtung mechanischer Rückkopplungen eröffnet zusätzliche Perspektiven, wie Zellen und Gewebe ihre Form an Umwelteinflüsse anpassen und geometrische Komplexität generieren. Ein weiterer spannender Aspekt ist, wie diese theoretischen Konzepte mit modernster Technologie verknüpft werden.
Hochauflösende Mikroskopie, 3D-Modellierung und Simulationen helfen Wissenschaftlern, die Vorgänge auf kleinster Ebene sichtbar zu machen und präzise nachzubilden. In Experimenten mit künstlichen elastischen Materialien lassen sich die Prinzipien der geometrischen Rückkopplung nachahmen und somit aus der Natur lernen. Die getrennte Betrachtung von Wachstum und Formgebung war lange Zeit Standard, doch diese Forschung verbindet die beiden Felder auf einzigartige Weise. Dieser interdisziplinäre Ansatz profitiert von Erkenntnissen aus Mathematik, Physik und Biologie und zeigt, wie komplex und raffiniert natürliche Prozesse tatsächlich sind. Die neue Entdeckung wirft zudem einen neuen Blick auf das Thema Musterbildung in der Natur.
Die punktigen Kanten der Rosenblätter oder die Rollen an ihren Rändern könnten als Beispiel für natürliche Optimierung gelten, bei der Struktur und Funktion voll in Einklang gebracht werden. Solche Formen können der Pflanze Vorteile verschaffen, etwa in Bezug auf Lichtaufnahme, Wasserabfluss oder Schutz vor Fressfeinden. Über die ästhetische Faszination hinaus hilft dieses Wissen dabei, die biologischen Muster besser zu verstehen und in technischen und künstlerischen Kontexten zu nutzen. Es eröffnet Möglichkeiten für Innovationen in der Architektur oder im Design, wo flexible, organische Formen zunehmend gefragt sind und präzise Steuerung der Formentwicklung notwendig ist. Die Untersuchung der mathematischen Grundlagen der Blütenblattform ist ein eindrucksvolles Beispiel, wie sich Wissenschaft und Schönheit der Natur ergänzen.
Die Rosenblätter sind nicht nur Schmuckstücke der Natur, sondern auch komplexe biologische Systeme, die durch faszinierende physikalische und mathematische Prinzipien entstehen. Die Entdeckung des bisher unbekannten geometrischen Feedbacks bei der Blütenblattentwicklung wirft eine Reihe spannender Fragen für zukünftige Forschung auf. Beispielsweise interessiert man sich für die molekularen Mechanismen, die jede Zelle veranlassen, auf die mechanischen Signale zu reagieren, oder wie diese Prinzipien bei anderen Pflanzenarten wirken. Zudem könnten die Erkenntnisse helfen, neue Wege in der synthetischen Biologie zu beschreiten – etwa bei der gezielten Formgebung von Organoiden oder pflanzlichen Bauelementen für Agrarwissenschaften. Dies könnte Auswirkungen auf die Landwirtschaft oder Biotechnologie haben, wenn man die natürliche Formbildung besser kontrollieren kann.