Neuronale Netzwerke sind inzwischen ein integraler Bestandteil moderner Technologie, von Spracherkennung bis hin zu Bildernkennung und autonomen Fahrzeugen. Die Grundlage für das Trainieren und Verstehen dieser komplexen Modelle liegt in sogenannten Autograd-Engines. Eine der bekanntesten und einfachsten Implementierungen eines solchen Systems stammt von Andrej Karpathy und nennt sich Micrograd. Besonders spannend wird es, wenn man diese Idee über die Grenzen von Python hinausträgt und beispielsweise in der Programmiersprache Go umsetzt. Dadurch entstehen frische Perspektiven auf Performance, Einfachheit und Lesbarkeit beim Entwickeln neuer Machine-Learning-Infrastruktur.
Doch bevor wir tiefer in die Materie eintauchen, lohnt es sich, das Fundament zu verstehen: Was sind neuronale Netzwerke überhaupt und warum braucht man Autograd? Ein neuronales Netzwerk kann man sich zunächst als eine Art Blackbox vorstellen. Man gibt Eingabewerte hinein und erhält eine Ausgabe. Anders als bei klassischen Funktionen, bei denen der genaue Ablauf klar definiert ist, lernt ein neuronales Netzwerk, wie es die Eingaben zu behandeln hat, anhand von Beispielen selbst. Wenn wir etwa eine Funktion „double(x) = 2x“ modellieren wollen, schreiben wir diese normalerweise direkt. Möchten wir aber, dass ein neuronales Netzwerk dies allein durch Beispiele erlernt, so geben wir ihm Paare von Eingaben und den zugehörigen Ergebnissen, und das Netzwerk erschließt sich die Regeln selbst.
Die Grundlage hierfür bildet die sogenannte Neuroneinheit, welche Eingaben mit zugehörigen Gewichten multipliziert, deren Summe mit einem Bias versehen und anschließend durch eine Aktivierungsfunktion geleitet wird. Aktivierungsfunktionen sind dabei von enormer Bedeutung, da sie nichtlineare Eigenschaften schaffen, die ein neuronales Netzwerk befähigen, komplexe Muster zu erkennen. Wird nur lineare Verarbeitung angewandt, wäre selbst ein mehrlagiges Netzwerk der Komplexität einer einzelnen Schicht gleich. Ob das einfache Modell mit nur einem einzelnen Neuron oder ein tiefes Netzwerk mit Millionen Neuronen – die Trainingsprozesse verwenden stets ähnlich gelagerte Prinzipien. Die zentrale Frage lautet, wie Gewichte so angepasst werden, dass das Netzwerk bessere Vorhersagen trifft.
Die Antwort liegt im Optimierungsverfahren namens Backpropagation. Hierbei wird der Fehler der Vorhersage über die meisten Parameter des Modells verteilt, sodass anhand der Gradientenrichtung die Gewichte aktualisiert werden. Das Berechnen dieser Gradienten, also der partiellen Ableitungen der Fehlerfunktion in Bezug auf die Gewichte, ist jedoch nicht trivial, erst recht in sehr großen Modellen. Hier kommen Autograd-Engines ins Spiel. Autograd-Engines übernehmen die automatische Differenzierung von Ausdrücken, welche aus zahlreichen Operationen und Variablen bestehen.
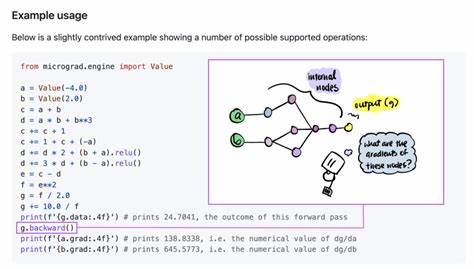
Das heißt, sie erstellen eine Darstellung der Rechenoperationen – meist als gerichteter azyklischer Graph – und berechnen die Ableitung jeder Variablen systematisch. Andrej Karpathys Micrograd ist ein minimalistisch entworfener Autograd-Engine in Python. Sie ist kompakt gehalten, umfasst nur einige hundert Zeilen Code und zeigt eindrucksvoll, wie Konzepte wie Vorwärts- und Rückwärtsdurchlauf implementiert werden können. Für Entwickler, die tiefer in die Mechanik eintauchen möchten, ist dieses Projekt ein wertvoller Einstieg. Die Entscheidung, Micrograd in Go neu umzusetzen, ist vor allem durch die Spracheigenschaften motiviert.
Go bietet einfache Syntax, effizientes Speicher-Management sowie hervorragende Performance, was sie gerade für hohe Anforderungen spannend macht. Zudem punktet Go durch seine statische Typisierung und robuste Toolchain. Die Implementierung basiert im Kern auf der Struktur Value, welche Skalare repräsentiert, ähnlich dem Value-Objekt in Karpathys Originalcode. Jede Value-Instanz hält einen Float64-Datenwert sowie Verweise auf vorherige Werte im Rechengraphen und die Operation, die zur Erstellung geführt hat. Dank dieses Designs entsteht bei der Verkettung von Operationen, etwa Addition und Multiplikation, ein gerichteter Graph, in welchem die Abhängigkeiten nachvollziehbar sind.
Für die Operationen Add und Mul werden jeweils neue Werte mit entsprechenden Elternknoten im Graph erzeugt, wodurch sich die gesamte Berechnungshistorie abbildet. Dieses Vorgehen bildet die Grundlage für die spätere Rückwärtsrechnung der Gradienten. Um Backpropagation zu ermöglichen, wird dem Value-Typ ein Gradientenfeld hinzugefügt, das während der Ableitungspfadberechnung schrittweise aktualisiert wird. Darüber hinaus wird ein Funktionstyp hinzugefügt, der die Rückwärtsrichtung für jede Operation beschreibt – diese minimieren entweder die Fehlerfunktion oder passen Gewichte präzise an. Die eigentliche Rückwärtsrechnung erfolgt über einen Topologie-Sortierungsalgorithmus, der sicherstellt, dass alle voneinander abhängigen Werte in der korrekten Reihenfolge verarbeitet werden.
Dies ist entscheidend, da Gradienten immer in umgekehrter Reihenfolge der Berechnung propagiert werden müssen. Im Beispiel des Trainings einer Funktion zum Verdoppeln wird ein einfacher Trainingsloop implementiert: Ausgangsgewichte werden zufällig initialisiert, gefolgt von Vorwärtsdurchlauf, zur Berechnung des Fehlers, danach erfolgt die Rückwärtsdurchführung des Gradsamen entsprechend des Verlustes, und zum Schluss werden Gewichte über eine Lernrate angepasst. Die Effizienz dieses Prozesses zeigt sich darin, wie der Verlust nach wenigen Iterationen rapide sinkt und sich die Gewichtswerte dem idealen Ziel nähern. Neben der minimalen Funktionalität bietet die Go-Implementierung weitere Vorteile. Die statische Typisierung des Codes verhindert viele Fehlerquellen, die bei dynamisch typisierten Sprachen auftreten können.
Das Aufbauen von Operationen als eigenständige Funktionen vereinfacht zudem Erweiterungen wie das Hinzufügen weiterer mathematischer Operationen oder komplexerer neuronaler Strukturen. Die semantische Nähe von Go an C macht den Code zudem leicht verständlich, sodass Entwickler aus verschiedenen Hintergründen schnell einsteigen können. Die Textausgabe der Rechengraphen in der Go-Version ersetzt Karpathys visuelle Diagramme und erlaubt es, den Verlauf der Operationen und deren Verknüpfungen auch in nichtgrafischen Umgebungen transparent zu machen. Dieses Feature ist besonders praktisch für Debugging und das Lernen der zugrundeliegenden Abläufe. Gleichzeitig bleibt die Umsetzung überschaubar und leicht anpassbar, was bei Anwendung in größeren Machine-Learning-Projekten von Vorteil ist.
Die Bedeutung einer derartigen Autograd-Engine erstreckt sich weit über einfache Demo-Projekte hinaus. Gerade bei groß skalierbaren Modellen mit Milliarden von Parametern ist direkte Ableitungshandhabung von wesentlicher Bedeutung für Training und Optimierungen. Damit werden neben Effizienz auch Flexibilität bei Anpassungen an neue Architekturen gewonnen. Das Nachprogrammieren eines solchen Systems fördert ein tiefes Verständnis der Mathematik hinter künstlichen neuronalen Netzwerken und automatischer Differenzierung. Für Entwickler und Forscher gleichermaßen bietet es eine Möglichkeit, neue Konzepte zu testen, ohne auf etablierte Frameworks angewiesen zu sein.
Gerade im Kontext von Go eröffnen sich hier mögliche neue Wege, um Machine-Learning-Workflows schlanker und performanter zu gestalten. Zusammenfassend lässt sich sagen, dass die Implementierung von Micrograd in Go einen lehrreichen und praxisorientierten Zugang zu automatischer Differenzierung darstellt. Sie verdeutlicht, wie man mit überschaubarem Code komplexe mathematische Prozesse abbilden kann und gleichzeitig die Vorteile moderner Programmiersprachen nutzt. Für jeden, der sich mit neuronalen Netzwerken beschäftigt, ist das Verständnis einer Autograd-Engine ein essenzieller Baustein, um die Grundlagen der Modelloptimierung wirklich zu erfassen. Von der Entstehung des Rechengraphen über den Vorwärts- und Rückwärtsdurchlauf hinweg bis zur Gewichtsanpassung bietet dieser Ansatz eine klare Struktur, die sowohl für kleinere als auch größere Machine-Learning-Projekte anwendbar ist.
Die Beschäftigung mit der Mikrograd-Implementierung in Go öffnet somit Türen zu tieferem mathematischen und programmiertechnischen Verständnis und stellt gleichzeitig eine solide Basis für weiterführende Entwicklungen in der KI dar.