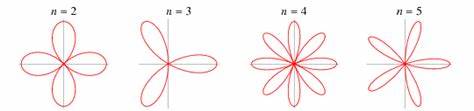
Die Schönheit der Natur steckt oft in den Details, und Rosenblätter gehören zweifelsohne zu den faszinierendsten Beispielen. Ihre zarten, oft spitz zulaufenden Kanten und die geschwungenen Formen ziehen seit Jahrhunderten die Aufmerksamkeit von Künstlern und Wissenschaftlern gleichermaßen auf sich. Was jedoch nur wenige wissen, ist, dass hinter dieser Ästhetik eine komplexe mathematische Grundlage steckt, deren Entdeckung erst kürzlich durch interdisziplinäre Forschung möglich wurde. Diese Entdeckungen zeigen, wie physikalische Kräfte und ein spezieller geometrischer Mechanismus das Wachstum der Blätter regulieren und ihre einzigartige Form schaffen. Die Forschung zu diesem Thema findet sich am Schnittpunkt von Biophysik, Mathematik und Entwicklungsbiologie und eröffnet neue Perspektiven darauf, wie komplexe Naturformen entstehen.
Die wissenschaftliche Arbeit, die dieser Erkenntnis zugrunde liegt, wurde erstmals 2025 veröffentlicht, als Forscher mithilfe theoretischer Analysen, Computermodellen und experimentellen Nachbildungen aus dehnbarem Kunststoff die Wachstumsmechanismen von Rosenblättern nachstellten. Dabei wurde festgestellt, dass ein bisher in der Natur unerkannter geometrischer Rückkopplungsprozess für die charakteristischen gekrümmten und spitzen Ränder verantwortlich ist. Die Blätter wachsen nicht einfach gleichmäßig, sondern reagieren mit einer Art mechanischem Feedback auf die Spannung, die durch ihr eigenes Wachstum entsteht. Dieses Feedback reguliert das Wachstum auf eine Weise, die zu mehrschichtigen und komplexen Musterbildungen führt. Mechanische Rückkopplung ist ein physikalisches Prinzip, bei dem eine entstandene Kraft oder Deformation eine Veränderung im System bewirkt, welche wiederum die ursprüngliche Ursache beeinflusst.
Im Fall der Rosenblätter bedeutet dies, dass das Wachstum an den Rändern durch die Krümmung und Spannung beeinflusst wird, die durch das Ausrollen der Blätter entsteht. Wenn sich ein Rosensblatt nach außen wölbt, erzeugen die inneren Schichten eine mechanische Spannung, die das Wachstum an bestimmten Punkten verstärkt oder hemmt. Dies führt dazu, dass sich die Blattränder wellenförmig biegen und spitz zulaufende Spitzen bilden, die vielen Rosen ihre charakteristische Optik verleihen. Die mathematischen Modelle, die diesen Prozess beschreiben, basieren auf Differentialgeometrie und Nichtlinearen Dynamiken. Sie ermöglichen es, die komplexen Formen der Blätter durch Berechnung von Krümmungen und Wachstumsraten zu simulieren.
Besonders bemerkenswert ist, dass die Forscher das für ein solches Wachstum nötige Feedback in klassischen Modellen bisher nie finden konnten. Die Entdeckung eines solchen geometrischen Feedbacks hingegen stellt einen völlig neuen Mechanismus vor, der weit über Pflanzenbiologie hinaus von Bedeutung sein könnte. Auch Experimente mit dehnbaren Kunststofffolien spielten eine essentielle Rolle dabei, die Theorie experimentell zu überprüfen. Die Forscher schnitten Folienstücke in Formen von Rosenblättern aus und simulierten das Wachstum durch kontrollierte Dehnung. Dabei bildeten sich ähnliche Wellen und Spitzen, die denen echter Rosenblätter verblüffend ähnlich waren.
Diese Ergebnisse untermauern, dass das Zusammenspiel von Wachstum und mechanischem Feedback tatsächlich die bemerkenswerten Formen der Blätter erzeugt. Diese Erkenntnisse werfen auch ein neues Licht auf die Entwicklung von Pflanzen und deren Morphogenese, also der Entstehung von Formen und Mustern während des Wachstums. Pflanzen verwenden mechanische Kräfte inzwischen als einen wichtigen Faktor bei der Formgebung. Während bisher biologisch-chemische Signale im Vordergrund standen, nimmt die Rolle biomechanischer Prozesse ständig zu. So zeigt sich, dass Pflanzenzellen beim Wachsen enormen physikalischen Kräften ausgesetzt sind und diese aktiv regulieren, um bestimmte Strukturen zu erzeugen.
Die ungewöhnliche Mathematik hinter den Rosenblättern ist ein exemplarisches Beispiel für diese faszinierende Dynamik. Darüber hinaus eröffnet diese Forschung auch ganz praktische Möglichkeiten in der Materialwissenschaft und Biomimetik. Die Prinzipien, mit denen sich komplizierte Formen durch mechanisches Feedback an der Oberfläche erzeugen lassen, könnten in der Herstellung von flexiblen Materialien, Robotik oder auch in der Architektur Anwendung finden. Die Fähigkeit, Formen mittels kontrollierter Spannungen selbstständig entstehen zu lassen, kann innovative Designkonzepte ermöglichen, die sich an der Natur orientieren. Für Liebhaber von Rosen und der Natur generell bedeutet diese Entdeckung eine Bereicherung des Verständnisses und eine neue Dimension, in der man die Schönheit der Blume betrachten kann.
Hinter den zauberhaften, samtigen Blättern liegt nicht nur ästhetisches Empfinden, sondern auch eine komplexe mathematische Ordnung, die uns zeigt, wie eng Kunst, Wissenschaft und Natur miteinander verbunden sind. Die Verbindung von Geometrie, Wachstum und physikalischem Feedback macht die Rose zu einem noch faszinierenderen Beispiel für die Wunder der natürlichen Welt. Zukünftige Forschungen werden aller Voraussicht nach noch tiefer in die Mechanismen und Variationen dieser Prozesse eintauchen und vielleicht weitere Pflanzenarten mit ebenso interessanten Formen untersuchen. Das Verständnis solcher Mechanismen könnte auch in der Landwirtschaft, der Gentechnik und bei der Entwicklung neuer biologischer Materialien entscheidend sein. Die Evolution hat durch einen so einzigartigen mathematischen Mechanismus etwas erschaffen, das zugleich kunstvoll und funktional ist – eine Inspiration für viele Wissenschaftsbereiche weltweit.
Die Studie des ungewöhnlichen mathematischen Mechanismus hinter der Form der Rosenblätter ist ein beeindruckendes Beispiel für die Verbindung von Theorie und Praxis. Sie zeigt, wie mithilfe von mathematischen Werkzeugen und physikalischen Experimenten eine tiefe Einsicht in biologische Prozesse gewonnen werden kann. Die Rosen als Symbol für Schönheit und Liebe erhalten so noch einen zusätzlichen Wert als Lehrmeister für die Schönheit der Mathematik in der Natur.