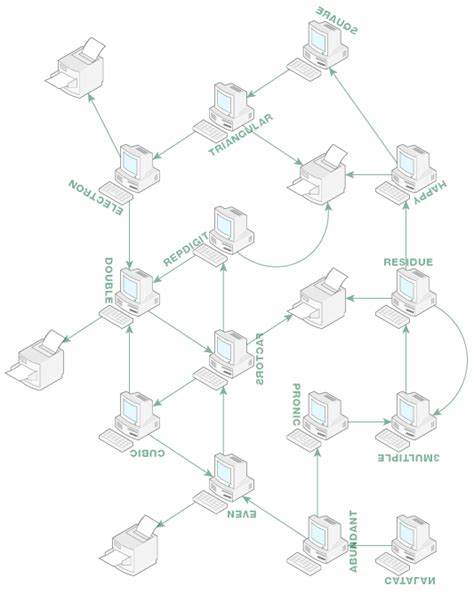
Der Melbourne University Puzzle Hunt 2013 präsentierte mit dem Rätsel Informatix eine außergewöhnliche Herausforderung, die viele Puzzle-Liebhaber und mathematisch Interessierte gleichermaßen in ihren Bann zog. Dieses Rätsel, inspiriert von der Comic-Welt von Asterix & Obelix, orientierte sich an einer der fiktiven Figuren namens Informatix – einem Experten für Datenverarbeitung, der es versteht, komplexe Netzwerke und vielschichtige Abläufe miteinander zu verknüpfen. Das Puzzle spielt im Rahmen eines durchdachten Spiels, das in mehreren Akten aufgebaut wurde, eine zentrale Rolle im zweiten Akt. Informatix steht dabei symbolisch für das Gedankengebäude hinter dem Rätsel, seine Neigung, Dinge zu überkomplexifizieren, spiegelt sich in der Konstruktion des Rätsels wider. Im Mittelpunkt stand ein Netzwerk, das aus Terminals und Druckern besteht und durch einen komplexen Satz an Regeln gesteuert wird.
Diese Regeln waren in einer übersichtlichen Tabelle aufgelistet, die die Übergänge zwischen den Elementen des Netzwerks beschrieb. Jeder Terminal hatte dabei unterschiedliche Bedingungen und Operationen, die auf eine ausgehende Druckauftragsnummer angewandt wurden, bevor sie an ein anderes Element weitergeleitet wurde. Die Schwierigkeit lag nicht nur in der Komplexität des Netzwerkes an sich, sondern vor allem darin, dass aus 14 einzigartigen Druckaufträgen mit Nummern von 1 bis 14 ein Muster ermittelt werden musste, das die beschriebenen Bedingungen erfüllt. Ein wichtiger Hinweis war dabei, dass 12 der Druckaufträge unverändert einen Drucker erreichten, während zwei Druckaufträge zu ihrem Ausgangsterminal zurückkehrten – ebenfalls ohne ihre Nummer verändert zu haben. Während des Lösungsprozesses wurde deutlich, dass sich das Problem in mehrere klar definierte Teilaufgaben gliedern ließ, bei denen zunächst Terminals mit begrenzten möglichen Druckauftragsnummern betrachtet wurden.
So ergaben sich beispielsweise für das Terminal SQUARE nur die Quadratzahlen 1, 4 und 9 als mögliche Startwerte, wobei Schlussfolgerungen aus den Bewegungen der Druckaufträge gezeigt haben, dass nur die Zahl 9 bei diesem Terminal passend ist. Ähnlich verhielt es sich bei anderen Terminals mit speziellen mathematischen Bedingungen, wie PRONIC, das rechteckige Zahlen verlangte, und CATALAN, welches nur bestimmte katalanische Zahlen zuließ. Auf diese Weise konnte Schritt für Schritt eine genaue Zuordnung der Druckaufträge zu den Terminals vorgenommen werden. Besonders interessant war die Art, wie die mathematischen Eigenschaften der Zahlen unmittelbar in die Netzwerklogik integriert wurden. So wurden nicht nur klassische Eigenschaften wie Gerade, Vielfache von drei oder Dreieckszahlen berücksichtigt, sondern auch spezielle Kategorien wie glückliche Zahlen (Happy Numbers), die sich durch eine charakteristische Iteration von Quadrieren und Summieren ihrer Ziffern auszeichnen, und sogenannte Repdigit-Zahlen, die ausschließlich aus sich wiederholenden Ziffern bestehen.
Das Terminal ELECTRON prüfte eine besondere physikalische Eigenschaft, nämlich die Anzahl der Elektronen in Atomschalen, womit dieser abstrakte mathematisch-logische Aufbau eine Verbindung zur realen Welt der Naturwissenschaften herstellte. Neben der mathematischen Analyse ermöglicht das theoretische Netzwerkmodell eine anschauliche Visualisierung des Druckauftragsverhaltens – jede durchlaufene Station bedeutete für die jeweilige Nummer eine bestimmte Transformation oder eine Prüfung, die den Weg der Jobs exakt definierte. Die graphische Darstellung des Netzwerks bot nicht nur Hilfestellung bei der Nachverfolgung der Prozessketten, sondern zeigte beim genauen Betrachten eine bemerkenswerte Besonderheit: die aufwendig gestalteten Terminalnamen, welche häufig invertiert, gespiegelt oder gedreht dargestellt waren, bildeten bei entsprechender Umkehrung Buchstaben des lateinischen Alphabets. Die einzelnen Buchstaben, geordnet nach den zugehörigen Druckauftragsnummern, ergaben als Lösungssatz das Wort „LAMBDA CALCULUS“. Diese Entdeckung verleiht dem Rätsel eine besonders tiefgründige Note, weil Lambda-Kalkül eine fundamentale Theorie der mathematischen Logik und der funktionalen Programmierung darstellt.
Die Lösung des Informatix-Rätsels ist somit nicht nur ein Beweis für logisches und mathematisches Denken, sondern auch für das kreative Kombinieren verschiedener Wissensbereiche. Sie zeigt beispielhaft, wie komplexe mathematische Konzepte in einem spielerisch-konstruierten Netzwerk zum Leben erweckt werden können. Liefert man die 14 Startnummern den jeweiligen Terminals zu, ergibt sich ein etabliertes Netz an Zuständen und Übergängen, das, obwohl kompliziert erscheinend, vollständig nachvollziehbar und widerspruchsfrei ist. Ausgehend von Terminals mit besonders restriktiven Bedingungen, konnte man den Suchraum stark einschränken und letztendlich zu einer eindeutigen Belegung gelangen. Die Aufgabe fordert den gelösten Druckaufträgen nicht nur eine Übereinstimmung mit den mathematischen Bedingungen ab, sondern auch die Konsistenz der gesamten Prozesskette und die Unveränderlichkeit der Auftragsnummern, sofern sie keinen Fehlerzustand (Fehlermeldung) hervorrufen.
Dieses Kriterium stellt sicher, dass alle Operationen korrekt angewandt werden und keine widersprüchlichen Resultate entstehen. Zudem wird sichergestellt, dass alle Operationen im Netzwerk mindestens einmal ausgeführt wurden, womit auch die Vollständigkeit und Breite der Lösung garantiert wird. Die Tatsache, dass die Auftragnummern jederzeit ganzzahlig zwischen 1 und 99 bleiben, sorgt zusätzlich für mathematische Eleganz und praktischen Realismus. Rückblickend bietet die komplexe Logik des Informatix-Puzzles nicht nur einen herausfordernden Denksport, sondern auch eine lehrreiche Erfahrung für alle, die sich für die Schnittstelle von Mathematik, Informatik und Rätselgestaltung interessieren. Die Kombination aus Zahlenmengen mit besonderen Eigenschaften, operativen Transformationen und Vernetzung macht das Rätsel zu einem hervorragenden Beispiel dafür, wie abstrakte mathematische Theorien auf kreative Weise greifbar und sichtbar gemacht werden können.
Darüber hinaus zeigt das Resultat „LAMBDA CALCULUS“, wie tief verwurzelt und interdisziplinär die Beziehungen zwischen mathematischer Logik und praktischer Problemlösung sind. Die Lösung des Puzzles Informatix vermittelt damit nicht nur eine technische Antwort, sondern schreibt eine kleine Geschichte darüber, wie Mathematik und Fantasie zusammen ein spannendes und bereicherndes Erlebnis schaffen können. Die umfangreiche Analyse des Rätsels verdeutlicht auch, dass gründliches strukturierendes Denken und eine systematische Annäherung oft der Schlüssel zum Lösen scheinbar unübersichtlicher Herausforderungen sind. Letztendlich steht Informatix stellvertretend für die Faszination von Puzzles, die weit mehr sind als einfache Denkspiele – sie sind Zugänge zu einem tieferen Verständnis von Mathematik, Informatik und deren kreativer Anwendung. Wer sich mit solcherart Aufgaben beschäftigt, schult nicht nur analytische Fähigkeiten, sondern auch Ausdauer und die Fähigkeit, verborgene Zusammenhänge zu erkennen.
Zusammenfassend bleibt festzuhalten, dass das Melbourne University Puzzle Hunt 2013 mit dem Informatix-Rätsel ein Meisterwerk präsentiert hat, das mathematische Logik, funktionale Programmierung, Zahlenmengen und Netzwerkprozesse auf ungewöhnliche und ansprechende Weise miteinander verbindet. Das Resultat ist eine Einladung an Wissbegierige, komplexe Strukturen zu erforschen und Lösungen zu erarbeiten, die über das Offensichtliche hinausgehen und die Schönheit der Mathematik in ihrer reinsten Form widerspiegeln.