Chaos fasziniert Wissenschaftler und Laien gleichermaßen. Begriffe wie der Schmetterlingseffekt sind in der Populärkultur allgegenwärtig und wecken die Vorstellung, dass kleinste Veränderungen im Anfangszustand eines Systems zu dramatisch unterschiedlichen Ergebnissen führen können. Doch wie chaotisch sind chaotische Systeme wirklich? Und wie gut können moderne Methoden, vor allem Künstliche Intelligenz (KI) im Bereich Scientific Machine Learning (SciML), diese Systeme vorhersagen? Diese Fragen stehen im Mittelpunkt vieler aktueller Forschungsarbeiten, deren Genauigkeitsansprüche oft kritisch betrachtet werden müssen. Ein chaotisches System ist durch eine Eigenschaft gekennzeichnet, die als sensitive Abhängigkeit von Anfangsbedingungen bezeichnet wird. Diese bedeutet, dass zwei nahezu identische Anfangswerte im Laufe der Zeit exponentiell auseinanderdriften, sodass Vorhersagen über längere Zeiträume hinaus grundsätzlich instabil und fehleranfällig sind.
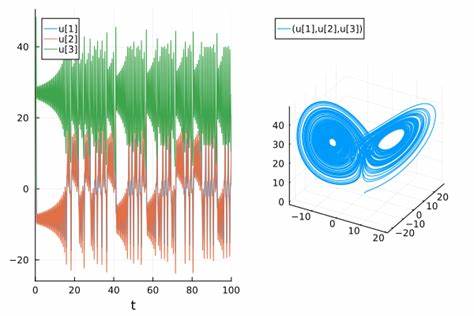
Ein Paradebeispiel für ein chaotisches System sind die Lorenz-Gleichungen, die das Verhalten atmosphärischer Konvektion modellieren und häufig zur Veranschaulichung chaotischer Dynamik genutzt werden. Das Problem bei der numerischen Lösung solcher Gleichungen liegt darin, dass selbst kleinste Rechenfehler oder Rundungsungenauigkeiten im Anfangszustand im Laufe der Integration exponentiell anwachsen können. So verändern winzige Variationen bei Parametern oder Anfangsbedingungen, die im Bereich der Maschinengenauigkeit liegen, das Ergebnis so drastisch, dass die resultierenden Trajektorien des Systems kaum noch miteinander vergleichbar sind. Ein Beispiel ist die Änderung eines Parameters von 10.0 zu 10.
000000000000001 in den Lorenz-Gleichungen, was nach einer bestimmten Zeit zu völlig unterschiedlichen Systementwicklungen führt. Ein weiterer wichtiger theoretischer Aspekt ist das sogenannte Shadowing-Lemma. Dieses besagt, dass eine numerisch berechnete Trajektorie zwar nicht exakt diejenige des ursprünglich spezifizierten Systems ist, wohl aber als Trajektorie eines anderen Systems mit leicht abweichenden Anfangsbedingungen interpretiert werden kann. Somit „schattet“ die berechnete Lösung eine echte Lösung eines nahen Systems nach. Dies erklärt, warum numerische Lösungen von chaotischen Systemen trotz inhärenter Ungenauigkeit dennoch ein sinnvolles Bild des chaotischen Attraktors vermitteln können – selbst wenn sie nicht die exakte Trajektorie darstellen.
Was bedeutet das für die Vorhersagefähigkeit von KI-Modellen? Viele wissenschaftliche Arbeiten nutzen neuronale Netze oder andere Machine-Learning-Techniken, um zeitliche Verläufe chaotischer Systeme vorherzusagen oder Parameter dieser Systeme aus Daten zu lernen. Dabei scheinen manche Veröffentlichungen sehr genaue Prognosen anzukündigen. Eine kritische Betrachtung zeigt jedoch, dass viele dieser Modelle mit numerischer Genauigkeit von 32-Bit-Fließkommazahlen auf modernen Grafikprozessoren arbeiten, was bei chaotischen Systemen bei weitem nicht ausreicht, um eine akkurate langfristige Vorhersage zu gewährleisten. Das Problem wird besonders deutlich, wenn man berücksichtigt, wie stark die Fehler im Zeitverlauf zunehmen. Für die Lorenz-Gleichung kann man nur etwa bis zu einem Zeitpunkt t=20 eine einigermaßen zuverlässige Trajektorie berechnen, bevor die Fehlergröße (der sogenannte O(1)-Fehler) dominierend wird und die Trajektorie auf dem chaotischen Attraktor quasi beliebig umherwandert.
Für längere Zeiten sind diese Modellvorhersagen so ungenau, dass sie eher eher zufälligen Punkten auf dem Attraktor entsprechen als der exakten Systemlösung. Wissenschaftliche Arbeiten, die ihre Modelle mit kurzen Zeitreihen oder Zeitspannen testen, die noch nicht von der chaotischen Sensitivität betroffen sind – beispielsweise nur bis t=3 oder t=10 bei Lorenz –, können leicht den Eindruck erwecken, sie hätten das chaotische System erfolgreich modelliert. Tatsächlich aber modellieren sie dann keine chaotischen Phänomene, da der exponentielle Fehlerverlauf noch nicht eingesetzt hat. Diese Diskrepanz wird besonders durch Beispiele wie das DeepXDE-Projekt oder Arbeiten mit neuronalen Differentialgleichungen sichtbar, die oft kurze Zeitintervalle wählen, in denen chaotisches Verhalten noch nicht auftritt. Daraus folgt, dass ihre hohen Genauigkeitsansprüche irreführend sind, da echte chaotische Prognosen deutlich komplexere und rechentechnisch aufwendigere Vorkehrungen erfordern.
Um präzise Trajektorien über längere Zeiträume vorherzusagen, sind hochpräzise numerische Verfahren mit speziellen Integratoren und erweiterten Fließkommazahlen (über 64-Bit hinaus, z.B. 128-Bit oder mehr) notwendig. Diese sind allerdings rechenintensiv, zeitaufwendig und meist auf Hochleistungsrechnern realisierbar. Selbst dann handelt es sich nicht um eine exakte „Vorhersage“, sondern eher um die Berechnung von Trajektorien, die sich einer Referenzlösung annähern.
Ein alternativer Ansatz, um dennoch Erkenntnisse über chaotische Systeme zu gewinnen, ist die fokussierte Analyse auf ergodische Eigenschaften. Diese mathematischen Eigenschaften beschreiben statistische Verteilungen von möglichen Zuständen anstelle genauer zeitlicher Entwicklungswege. Das Lernen und Vorhersagen solcher statistischen Kenngrößen ist realistischer, da diese stabiler gegenüber der Sensitivität von Anfangsbedingungen sind und daher von KI-Methoden potenziell besser erfasst werden können. Ein Beispiel hierfür ist die Sparse Identification of Nonlinear Dynamical Systems (SINDy)-Methode, die es ermöglicht, die zugrunde liegenden Gleichungen eines chaotischen Systems aus hochfrequenten, rauscharmen Daten zu rekonstruieren, ohne für lange Zeiträume vorwärts zu integrieren. Dadurch vermeidet SINDy die Problemfelder der exponentiell anwachsenden Fehler über Integration und arbeitet direkt mit lokalem Zustands-Datenmaterial.
Ähnlich zeigen neuere Forschungen, dass sogenannte Physics-Informed Neural Networks (PINNs) bei chaotischen Systemen dazu neigen, durch Verschiebung der Anfangsbedingungen eine unkompliziertere, physikalisch korrekte, aber nicht unbedingt reale Lösung zu approximieren. Das ist ein indirekter Wirkmechanismus des Shadowing-Lemmas und verdeutlicht weitere Grenzen beim Versuch, chaotische Trajektorien präzise mithilfe von KI vorherzusagen. Die weit verbreitete Überschätzung der Genauigkeit von KI für chaotische Systeme rührt zum Teil auch daher, dass viele Forscher und Reviewer die komplexen numerischen und theoretischen Anforderungen nicht hinreichend berücksichtigen. Dies ist kein Vorwurf an die Wissenschaftler, sondern eher ein Hinweis, wie schwierig dieses Gebiet ist und wie sorgfältig Interpretationen und Aussagen zu Chaospredictability gehandhabt werden müssen. Das Fazit ist klar: Langfristige Vorhersagen der genauen zeitlichen Entwicklung chaotischer Systeme sind selbst mit modernster KI und numerischer Technik derzeit unmöglich.
Die intrinsische Natur der Sensitivität bei chaotischen Systemen setzt fundamentale Grenzen. Stattdessen sollte der Forschungsfokus auf der Vorhersage von statistischen Eigenschaften und Ergodizitätsmaßen liegen, die trotz Chaos stabile und vorhersagbare Merkmale darstellen. Zukunftsfähige Entwicklungen im Scientific Machine Learning werden daher Methoden erforschen und optimieren, die das volle Potenzial von KI nutzen, um Wahrscheinlichkeitsverteilungen, Attraktoreigenschaften oder Langzeitstatistiken chaotischer Systeme zu lernen. Hierbei sind Konzepte aus der Differenzierbaren Programmierung, der erweiterten numerischen Präzision und der robusten Optimierung von zentraler Bedeutung. Zusammenfassend zeigt sich, dass Chaos zwar theoretisch deterministisch ist, aber praktisch durch seine sensible Abhängigkeit von Anfangsbedingungen Vorhersagen über längere Zeiträume entsprechend schwierig macht.
Die beeindruckenden Ergebnisse von KI für chaotische Systeme, die derzeit die Runde machen, sollten stets kritisch hinterfragt und in den Kontext begrenzter Zeitspannen und numerischer Genauigkeiten gesetzt werden. Die Herausforderung und Schönheit dieses Themenfeldes liegt genau darin, chaotische Dynamik besser zu verstehen, realistische Grenzen der Vorhersagbarkeit zu respektieren und innovative Methoden zu entwickeln, die über reine zeitliche Vorhersagen hinausgehen und erforschen, wie KI zur Analyse von chaotischen Systemen beitragen kann, ohne dabei überspezifizierte oder irreführende Versprechen zu machen.