Effiziente Implementierung von komplexen Zahlen und FFT allein mit Datentypen

Nachrichten zu Krypto-Börsen Steuern und Kryptowährungen

Im Bereich der numerischen Mathematik und funktionalen Programmierung stellt die Implementierung komplexer Zahlen und der Fast Fourier Transform (FFT) oft eine Herausforderung dar. Klassisch werden solche Berechnungen mit Gleitkommazahlen durchgeführt, was zwar performant ist, aber in bestimmten Anwendungen, etwa in formalen Beweissystemen oder optimierenden Compilern, problematisch sein kann. Hier setzt der Ansatz an, komplexe Zahlen und FFT rein mit algebraischen Datentypen abzubilden – also ohne native Fließkommazahlen, sondern mit rein funktionalen Konstruktionen. Dieser Weg reduziert nicht nur Ineffizienzen, sondern fördert auch optimale Ausführungsstrategien und erleichtert mathematische Beweise über Programme. In traditionellen Programmen gelten Fließkommazahlen meist als selbstverständlich.

Doch nutzen Entwickler in speziellen Umgebungen, beispielsweise Beweisassistenten wie Coq, oder in optimierenden virtuellen Maschinen, keine nativen Maschinentypen. Dort werden Zahlen oft als datentypische Strukturen modelliert, was die formale Verifikation erleichtert und extrem feingranulare Kontrolle über die Ausführung erlaubt. Dennoch sind solche algebraischen Umsetzungen meist langsamer, wenn die zugrundeliegende Rechenstruktur nicht sorgfältig gestaltet ist. Dies gilt auch für den FFT-Algorithmus, der eine der wichtigsten Operationen der Signalverarbeitung darstellt. Um neben korrekter Funktionalität auch eine möglichst effiziente Ausführung zu gewährleisten, muss man bestimmte klassische Umsetzungsfehler vermeiden.

So ist es etwa nicht optimal, in der FFT mehrfach Listen zu traversieren, diese aufzuspalten und Zwischenergebnisse mehrfach zu kopieren. Eine naive Implementierung mit Listen verursacht mehrfaches Traversieren und Kopieren, das kostet Zeit und verhindert die sogenannte Fusionsoptimierung. Die Fusionsoptimierung verwandelt Kettungen von Operationen, beispielsweise auf Listen, in eine einzige Traversierung. Wird sie unterbrochen, sinkt die Effizienz drastisch. Ein weiterer Nachteil ist der Gebrauch von Gleitkommazahlen als Element in komplexen Zahlen, die ebenfalls Fusionsmechanismen behindern.

Die Verbesserung beginnt mit der Verwendung balancierter Binärbäume anstelle von Listen. Diese Bäume kodieren die Indizes der Elemente in binärer Form, sodass die Zerlegung in gerade und ungerade Positionen jederzeit in konstanter Zeit möglich ist. Indem man für jeden Knoten einen linken und rechten Unterbaum verwendet, entspricht der Pfad von einem Blatt bis zur Wurzel genau der Binärrepräsentation seines Index. So lässt sich das klassische even/odd-Splitting durch einfaches Verschieben im Baum ersetzen. Auf diese Weise wird hoher Overhead vermieden und die Algorithmen können effizienter rekursiv funktionieren, wobei die Teilbäume direkt „Alright“ und „Odd“ repräsentieren.

Parallel dazu wird die Operation der Multiplikation mit sogenannten „Twiddle-Faktoren“ effizienter umgesetzt. Anstatt Kosinus-, Sinus- und Exponentialfunktionen direkt auf Fließkommazahlen anzuwenden, können algebraische Strukturen auf den komplexen Zahlenebenen verwendet werden. Die Implementierung basiert auf der erweiterten Darstellung der komplexen Zahlen durch algebraische Datentypen, beispielhaft über sogenannte Gaußsche Zahlen und ihre Erweiterungen. Gaußsche Zahlen ergeben sich aus der Verknüpfung zweier Integer-Typen und erweitern den Zahlenraum um die imaginäre Einheit i. Diese können direkt durch einen Baum ausbalancierter Natur modelliert werden, bei dem jeder Knoten weitere Integer oder Gaußsche Zahltypen enthält.

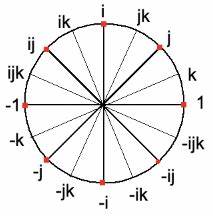
Die Verallgemeinerung führt zu erweiterten Gaußschen Zahlen, die zusätzliche Einheiten wie j und k berücksichtigen – dabei liegen tieferliegende algebraische Strukturen zugrunde, die vielfache Einheiten kombinieren und somit Mehrdimensionalität der komplexen Zahlen mit ganzzahliger Struktur möglich machen. Diese Zahlentypen ermöglichen es, die bekannten komplexen Wurzeln der Einheitskreise, die in FFT benötigt werden, exakt darzustellen, ohne auf Fließkommarepräsentationen zurückzugreifen. Stattdessen werden sie als ausbalancierte Baumstrukturen modelliert und durch einfache Rotations- und Negationsoperationen manipuliert. Dies führt zu einer radikalen Vereinfachung der inneren Multiplikationsoperation, die sich als rekursive Baumoperation formulieren lässt. Die Rotation entspricht dabei einem zyklischen Verschieben der Baumkomponenten mit Vorzeichenwechsel, wodurch Multiplikation mit imaginären Einheiten elegant und performant umgesetzt wird.

Der Vorteil dieser rotierenden multiplikativen Operation liegt darin, dass sie sich durch einfache wiederholte Anwendung (beispielsweise mehrfaches Rotieren) auf unterschiedliche Twiddle-Faktoren anwenden lässt. Die sonst oft komplexen Berechnungen von cos, sin und komplexen Exponentialfunktionen entfallen damit komplett, was die Transformation rein algebraisch macht. Das wiederum erlaubt vollständige Fusionsoptimierung und eliminiert unnötige Zwischenschritte. Somit sind die transformierenden Funktionen sehr kurz und verständlich und eignen sich ausgezeichnet zur Implementierung in rein funktionalen und formalen Programmiersprachen. Ein weiterer Nutzen des Baumtyps mit erweitertem Integer-ähnlichen Zahlenraum ist die Modularität.

Verschiedene Tiefen dieser Bäume stehen für verschiedene Ebenen der Genauigkeit oder Komplexität der FFT, die angewendet werden kann. Die Basis sind normale Integer; Gaußsche Ganzzahlen bilden eine etwas höhere Ebene. Höhere Dimensionen erlauben dann FFTs auf größerem Eingabespektrum mit komplexen Wurzeln höherer Ordnung. Die Anzahl der Blätter in solchen Bäumen wächst exponentiell mit der Tiefenstufe, doch Layout und Operationen sind so gestaltet, dass in konfliktfreien, optimalen Evaluationskonzepten diese exponentielle Größe nicht zu tatsächlicher Laufzeitexplosion führt, da Bäume homogen strukturiert und maximal geteilt werden können. Dies öffnet Wege zur Implementierung hochperformanter FFTs auf rein algebraischer Basis.

Die Rekursion selbst wird weiter modularisiert. Durch die Baumstruktur entfallen kostenintensive Operationen wie das Ermitteln der Listengröße oder das Teilen der Struktur in ungerade/gerade Indizes. Stattdessen lässt sich sehr elegant eine Funktion definieren, die die Baumtiefe beziehungsweise den Pfad als natürlichen Zahlentyp modelliert und als Argument mit herumgereicht wird. Das ermöglicht eine effiziente Steuerung der Rekursion und der erforderlichen Rotationen zum Einstreuen der Twiddle-Faktoren. Diese natürliche Darstellung, häufig in Church-Nat-Typen oder alternativen algebraischen Zahlendarstellungen, erlaubt zudem weitere Fusionsoptimierung in rein funktionalen Implementierungen.

Die Inverse FFT (IFFT) stellt allerdings noch eine größere Herausforderung dar. Aufgrund der komplexeren Additionen und der Notwendigkeit von Divisionen durch die Anzahl der Punkte (was Typen ohne native Gleitkommazahlen erschwert), sind aktuell noch keine optimale, fusionsfreundliche Implementierungsmöglichkeiten vollständig erarbeitet. Erste Ansätze zeigen, dass die Verwendung gleicher algebraischer Strukturen auch hier möglich ist, doch erfordern diese ein eigenes Design von Operationen, die präzise und zugleich effizient genug sind, um die ursprüngliche Komplexität nicht zu erhöhen. Dennoch ermöglicht die vorgestellte FFT-Implementierung bereits viele Anwendungen, bei denen Form- und Korrektheitsbeweise wichtiger sind als maximale Performance auf klassischen Maschinen. Diese neue Sichtweise auf die FFT-Implementierung mit rein algebraischen Datentypen erlaubt es Programmierern und Forschern, numerische Algorithmen und komplexe Zahlen innerhalb funktionaler oder verketteter Evaluationsmodelle zu realisieren, ohne auf native Fließkommarechenwerke angewiesen zu sein.

Dadurch wird ein enormes Potential für hochoptimierte, formale und mathematisch beweisbare Algorithmen eröffnet. Zusätzlich bietet sich die Möglichkeit, diese Strukturen noch weiter zu verallgemeinern. Beispielsweise kann die FFT als spezielle Form der sogenannten linearen kanonischen Transformation angesehen werden, die noch umfassendere Anwendungsmöglichkeiten in der Signalverarbeitung und mathematischen Physik bietet. Die hier vorgestellten Getter- und Setter-Funktionen für Bäume sowie die Rotationsmechanismen können dabei als Bausteine für eine größere Klasse algebraischer Operationen dienen. Darüber hinaus wurde in neueren Arbeiten und Implementierungen gezeigt, dass diese ausbalancierten Baumtypen und algebraischen Operationen auf komplexen Zahlen auch in optimierenden virtuellen Maschinen wie HVM (Higher-Order Virtual Machine) gut fusionsfähig sind.

Hierdurch wird trotz der vermeintlich hohen Komplexität eine effiziente Ausführung realisiert, die asymptotisch mit klassischen FFT-Implementierungen konkurriert und dabei formale Verifizierbarkeit beibehält. Ein wichtiges weiteres Merkmal in den entwickelten Algorithmen ist die geometrische Interpretation der Zahlen: Sie nutzen implizit die symmetrischen Eigenschaften der Wurzeln der Einheit, der algebraischen Erweiterungen und deren Multiplikation als Rotationen auf dem Einheitskreis. Diese Interpretation unterstützt die Eleganz der reinen Datentypen-Transformationen und erklärt, warum sich solche Algorithmen ohne Gleitkommaoperationen implementieren lassen. Die Balance zwischen theoretischer Eleganz und praktischer Leistungsfähigkeit bleibt eine der faszinierendsten Fragen dieser Herangehensweise. Durch die exakte Modellierung der Zahlen und Transformationen mit algebraischen Datentypen ist es möglich, die Grenzen zwischen abstrakter Mathematik, Programmierung und optimierendem Compilerdesign zu überschreiten.

Viele Herausforderungen erfordern noch Forschung, doch der bereits erzielte Fortschritt zeigt, dass es nicht nur akademisch interessant, sondern auch praktisch relevant ist. Abschließend bleibt der Ausblick spannend: Während bisherige FFT-Implementierungen auf nativen Datentypen mit Fließkommazahlen basieren, ermöglichen die hier erläuterten Konzepte die vollständig algebraische Modellierung komplexer Zahlenräume und ihrer Transformationen. Solche Implementierungen können in sicherheitskritischen Anwendungen, Beweissystemen und innovativen Compilertechniken einen signifikanten Beitrag leisten. Gleichzeitig eröffnen sie neue Wege zur Erforschung der optimalen Ausführung von numerischen Algorithmen in funktionalen, beweisorientierten und verketteten Rechenumgebungen.