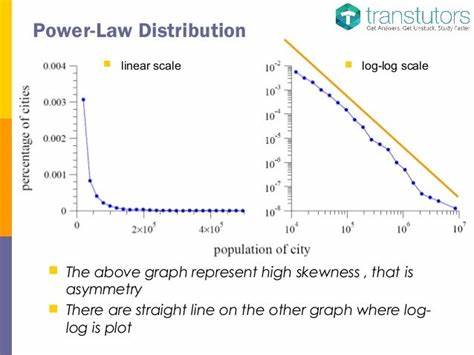
Gesetze, Potenzgesetze und Statistiken: Die Bedeutung der datenbasierten Wissenschaft In einer Welt, in der Daten unsere Entscheidungen leiten und unser Verständnis der Realität zunehmend prägen, steht die Analyse von Statistiken und deren Interpretationen im Mittelpunkt der wissenschaftlichen Diskussion. Wenn wir von Gesetzen und Potenzgesetzen sprechen, denken wir oft an abstrakte mathematische Konzepte. Doch diese Konzepte haben tiefgreifende Bedeutung für die Art und Weise, wie wir Phänomene in der Natur und der Gesellschaft verstehen. Insbesondere das Arbeiten mit Statistiken ist für die Wissenschaft von entscheidender Bedeutung, da es uns ermöglicht, Hypothesen zu überprüfen und zu validieren. Das Potenzgesetz, oft illustriert durch einfache Formeln, beschreibt Phänomene, bei denen eine bestimmte Größe in einer inversen Beziehung zu einer anderen steht.
Ein bekanntes Beispiel ist das Gutenberg-Richter-Gesetz, das die Verteilung von Erdbebenstärken beschreibt. Es zeigt, dass größere Erdbeben seltener auftreten als kleinere, und dass die Wahrscheinlichkeit, ein bestimmtes Ereignis zu beobachten, sich auf die Größe des Ereignisses zurückführen lässt. Solche Gesetze erscheinen in vielen Bereichen der Naturwissenschaften, von der Physik über die Biologie bis hin zur Soziologie. Der Umgang mit Daten ist jedoch alles andere als unkompliziert. Oft sind die experimentellen Ergebnisse widersprüchlich oder die Daten sind einfach nicht ausreichend, um eindeutige Schlussfolgerungen zu ziehen.
Wissenschaftler sind daher gefordert, ihre Daten nicht nur zu sammeln, sondern sie auch kritisch zu analysieren und zu interpretieren. Die Herausforderung besteht darin, zwischen echten Mustern und zufälligen Schwankungen zu unterscheiden – eine Aufgabe, die durch die Anwendung falscher statistischer Methoden erschwert werden kann. Ein auffälliges Beispiel dafür ist der häufige Einsatz von linearer Regression. Diese Methode, die darauf abzielt, die beste Anpassung für eine Datenreihe zu finden, kann in der Praxis zu verzerrten Ergebnissen führen, besonders wenn die ursprünglichen Daten logarithmisch transformiert wurden. Das Problem dabei ist, dass lineare Regression bei der Annahme von unabhängig verteilten Fehlern arbeitet.
Nach einer Transformation sind diese Annahmen jedoch oft nicht mehr gültig, was dazu führen kann, dass Wissenschaftler zu falschen Schlussfolgerungen gelangen. Die Arbeit von Aaron Clauset und seinen Kollegen im Jahr 2007 hat in diesem Kontext große Aufmerksamkeit erregt. Sie argumentierten, dass die Analyse von Potenzgesetzen eine höhere statistische Raffinesse erfordert. Sie entwickelten Methoden, um die Wahrscheinlichkeit zu bestimmen, mit der die beobachteten Daten aus einem Potenzgesetz hervorgehen könnten. Ihr Ansatz verknüpft die klassische Hypothesenprüfung mit der Analyse der spezifischen Eigenschaften der Potenzgesetze und bietet eine robustere Grundlage, um die Validität dieser Gesetze zu bewerten.
Die Implementierung solcher fortschrittlichen statistischen Methoden ist entscheidend, um die Wissenschaft von den Fesseln des Wishful Thinkings zu befreien. Oft neigen Wissenschaftler dazu, ihre Theorien durch die Linse ihrer Erwartungen zu betrachten, was zu einer selektiven Wahrnehmung von Daten führen kann. Clauset et al. forderten dazu auf, die Hypothese rigoros zu testen. Auch wenn die Daten zunächst eine Übereinstimmung mit einem Potenzgesetz zeigen, bedeutet das nicht automatisch, dass das Gesetz tatsächlich gilt.
Um die Argumentation zu festigen, müssen die Daten im Vergleich zu anderen Verteilungen geprüft werden. Ein weiterer wichtiger Aspekt der Diskussion über Potenzgesetze ist das Phänomen der Skalierbarkeit, das in vielen Bereichen beobachtet wird. Ein Beispiel hierfür ist die Verteilung der Wealth oder des Reichtums in einer Gesellschaft. Diese folgt oft einem Potenzgesetz, deutet jedoch auch auf eine Ungleichverteilung hin, die tiefere gesellschaftliche Implikationen hat. Wenn wir diese Daten korrekt analysieren, können wir besser verstehen, welche Faktoren zu sozialer Ungleichheit beitragen und wie diese beseitigt werden können.
In anderen Bereichen, wie beispielsweise der Epidemiologie, spielen Statistiken ebenfalls eine entscheidende Rolle. Bei der Analyse von Krankheitsausbrüchen oder der Bewertung von Medikamenten ist es unerlässlich, die zugrunde liegenden Daten genau zu betrachten. Falsche Schlüsse aus unzureichenden Daten können katastrophale Folgen haben, sowohl für die öffentliche Gesundheit als auch für die politische Entscheidungsfindung. Daher müssen Wissenschaftler und Entscheidungsträger eng zusammenarbeiten, um sicherzustellen, dass die verwendeten Daten vollständig und verlässlich sind. Ein weiterer interessanter Aspekt ist die Nutzung von Big Data in modernen wissenschaftlichen Disziplinen.
Mit der Verfügbarkeit riesiger Datenmengen haben Wissenschaftler die Möglichkeit, Muster zu erkennen, die vorher unentdeckt blieben. Dennoch bleibt die Herausforderung bestehen, diese Daten richtig zu interpretieren. Die Gefahr der Überanpassung, bei der Modelle gefunden werden, die die Daten „überanpassen“, ist nach wie vor aktuell. Dies erfordert ein erhöhtes Bewusstsein und Verständnis für die statistischen Methoden, die zur Analyse dieser Daten verwendet werden. In der heutigen Zeit, in der die Datenanalytik immer mehr zur Grundlage wirtschaftlicher und gesellschaftlicher Entscheidungen wird, ist es unerlässlich, die Prinzipien der Statistiken und Gesetze zu verstehen.
Nicht nur in der theoretischen Physik oder Biologie sind diese Konzepte von Bedeutung, sondern sie durchdringen auch unsere sozialen und ökonomischen Strukturen. Daher müssen wir sicherstellen, dass wissenschaftliche Integrität gewahrt bleibt und dass Datenanalysen nicht in der Erwartungshaltung gefangen sind. Abschließend lässt sich sagen, dass die Analyse von Gesetzen, Potenzgesetzen und Statistiken nicht nur eine technische Übung ist, sondern ein integraler Bestandteil der wissenschaftlichen Methodik. Indem wir diese Konzepte verstehen und kritisch anwenden, können wir zu einer fundierteren, datengestützten Entscheidungsfindung gelangen. Der Weg zur Wahrheit ist nicht immer geradlinig, aber eine rigorose statistische Analyse kann uns helfen, die Illusionen des Wunschdenkens zu durchbrechen und ein klareres Bild der Realität zu gewinnen.
Es ist die Verantwortung der Wissenschaftler, dieser Herausforderung gerecht zu werden und die Grundlagen für ein besseres Verständnis der Welt zu legen.