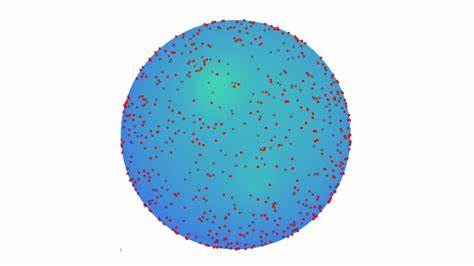
Die Erzeugung zufälliger Punkte auf einer Kugel ist eine Aufgabe, die in zahlreichen Bereichen wie der Kartografie, Computergrafik, Statistik, Physik und Computerwissenschaften von großer Bedeutung ist. Das scheinbar einfache Problem, Punkte zufällig und gleichmäßig auf einer Kugeloberfläche zu verteilen, birgt überraschende Herausforderungen. Die Komplexität entsteht vor allem durch die Krümmung der Oberfläche und die damit verbundenen geometrischen Eigenschaften, die Einfluss auf die Dichte der Punkteverteilung haben. Diese besondere Herausforderung fordert durchdachte Methoden, um eine faire und ästhetische Verteilung der Punkte zu erzielen. Der Weg zur optimalen Lösung führt über das Verständnis der sphärischen Koordinaten, deren eigene Tücken und die verschiedenen Ansätze, welche Forscher und Entwickler im Laufe der Jahre entwickelt haben.
Die erste und naheliegende Methode besteht darin, sphärische Koordinaten wie Längengrad (λ) und Breitengrad (φ) gleichmäßig aus einem bestimmten Bereich zu wählen. Typischerweise wird für den Längengrad λ ein Wert aus dem Intervall von -180° bis 180° und für den Breitengrad φ aus einem Intervall von -90° bis 90° ausgewählt. Auf den ersten Blick wirkt diese Methode intuitiv und einfach zu implementieren. Jedoch führt genau diese Herangehensweise zu einer ungleichmäßigen Verteilung der Punkte, bei der sich eine Konzentration der Punkte in Polnähe bildet. Praktisch ist dies bei der Abbildung von Erdbeobachtungen ein Problem, da Pole viel dichter mit Punkten bedeckt sind als Äquatorregionen, was zu Verzerrungen bei der Datenauswertung und Visualisierung führt.
Die ursächliche Erklärung für das Phänomen liegt in der unveränderlichen Geometrie der Kugeloberfläche. Je näher man an den Polen ist, desto kleiner werden die Flächenabschnitte, die durch bestimmte Bereiche der Breiten- und Längengrade definiert werden. Während am Äquator ein Winkelbereich von Δλ und Δφ ungefähr einer gleich großen Fläche entspricht, schrumpfen diese „Quadrate“ am Rand der Kugel signifikant. Dies führt dazu, dass bei gleichem Zufallsauswahlverfahren mehr Punkte in kleineren Flächenbereichen zusammenfallen, sodass eine ungewollte Verteilung entsteht. Um dieses Problem zu lösen, ist es notwendig, das Auswahlverfahren der Koordinaten anzupassen.
Ein bewährter Ansatz besteht darin, den Längengrad λ weiterhin gleichmäßig aus dem Intervall [-180°, 180°) zu wählen, während der Breitengrad φ nicht direkt, sondern über eine transformierte Zufallsvariable bestimmt wird. Diese Transformation basiert darauf, die Fläche des Kugelsegments zu berücksichtigen und somit die Punkte so zu verteilen, dass jede gleiche Fläche die gleiche Wahrscheinlichkeitsdichte an Punkten erhält. Eine effektive Methode beruht darauf, eine Zufallsvariable x aus dem Intervall [0, 1) zu ziehen und daraus den Breitengrad mit der Formel φ = cos⁻¹(2x - 1) zu berechnen. Dieses Vorgehen stellt sicher, dass die Punkte gleichmäßig über die gesamte Oberfläche verteilt sind und keine Clusterbildung an den Polen entsteht. Diese mathematische Herleitung sorgt für mehr Gleichgewicht in der Verteilung.
Dennoch ist die räumliche Verteilung durch dieses Verfahren nicht immer ästhetisch ideal. Zwar ist die Dichte über die gesamte Kugel ungefähr gleich, aber die Anordnung der Punkte kann unregelmäßig wirken. Insbesondere können einige Punkte zu nahe beieinander liegen, während andere größere Lücken bilden. Diese unregelmäßige Platzierung kann bei Anwendungen stören, bei denen eine harmonische und optisch angenehme Verteilung gewünscht ist, etwa bei der Gestaltung von Punktmuster für computergenerierte Oberflächen oder bei der Verteilung von Sensoren auf einer Kugeloberfläche. Um beispielsweise bei Visualisierungen oder Simulationen bessere Ergebnisse zu erzielen, wird häufig auf Verfahren zurückgegriffen, die nicht nur auf einer gleichmäßigen Wahrscheinlichkeitsverteilung beruhen, sondern auch eine Mindestabstandsbedingung zwischen den Punkten garantieren.
Eine solche Technik ist das sogenannte Poisson-Disc-Sampling, welches ursprünglich für zweidimensionale Flächen entwickelt wurde, sich jedoch erfolgreich auf sphärische Oberflächen übertragen lässt. Diese Methode verhindert, dass Punkte näher als ein vorgegebener minimaler Abstand zueinander liegen, wodurch eine übermäßig dicht gedrängte oder zu unregelmäßige Verteilung vermieden wird. Das Poisson-Disc-Sampling zeichnet sich durch seine besondere Eigenschaft aus, ähnlich einem sogenannten Blaurauschen („Blue Noise“) zu wirken. Das bedeutet, Clustering und große Leerräume zwischen den Punkten werden vermieden, so entsteht eine optisch sehr ansprechende und ausgeglichene Punktverteilung. Allerdings führt diese Methode technische Herausforderungen mit sich, da die Punkte nicht mehr unabhängig voneinander erzeugt werden.
Die Platzierung eines jeden Punktes richtet sich nach bereits vorhandenen Positionen, was die Komplexität des Algorithmus erhöht. Eine bekannte und pragmatische Variante zur Annäherung an ein Poisson-Disc-Sampling auf der Kugeloberfläche ist Mitchells Best-Candidate-Algorithmus. Bei diesem Algorithmus werden für jeden neuen Punkt mehrere Kandidaten generiert, von denen jener ausgewählt wird, der am weitesten von allen bereits existierenden Punkten entfernt ist. Obwohl diese Methode selbst keine perfekte Gleichmäßigkeit garantiert, erzielt sie in der Praxis oft sehr gute Ergebnisse und ist relativ einfach zu implementieren. Der Wert der gleichmäßigen oder gut verteilten Punkte auf einer Kugel lässt sich an unterschiedlichsten Beispielen verdeutlichen.
In der Kartografie ist es essenziell, um Datenpunkte gleichmäßig über die Erdoberfläche darzustellen, etwa bei der Visualisierung von Klimadaten. In der Astrophysik werden zufällige Punkte auf einer Himmelskugel genutzt, um Sterne oder andere astronomische Objekte zu simulieren oder zu vermessen. In der Computergrafik sind solche Verteilungen wichtig für die Gestaltung von Texturen, Umgebungslicht oder der Simulation von Partikelsystemen. Darüber hinaus sind in der statistischen Physik und in der Molekulardynamik zufällige Punktverteilungen auf Kugeloberflächen erforderlich, um Orientierungsmuster oder Eisensätze zu modellieren. Ebenso kommen sie beim Strahlen- oder Monte-Carlo-Rendering zur Anwendung, das Verfahren zur Erzeugung realistischer Licht- und Schatteneffekte nutzt diese gleichmäßigen Verteilungen, um Rechenzeit zu optimieren und Ergebnisse zu verbessern.
Weiterführend ist zu erwähnen, dass sich das Konzept der gleichmäßigen Verteilung auf einer Kugel noch auf andere Oberflächen verallgemeinern lässt, darunter Ellipsoide oder andere komplexe geometrische Formen. Insbesondere bei unregelmäßigen oder verformten Oberflächen erfordern die Verteilungsmethoden eine angepasste mathematische Behandlung und oft aufwändigere Algorithmen. Die Herausforderung der zufälligen Punktverteilung auf Kugeloberflächen ist somit vielseitig und interdisziplinär. Von einfachen Zufallsauswahlen bis hin zu komplexen Algorithmen wie dem Poisson-Disc-Sampling bieten die unterschiedlichen Ansätze jeweils verschiedene Vorteile und eignen sich für unterschiedliche Einsatzgebiete. Einen idealen Kompromiss zwischen Gleichmäßigkeit, Effizienz und einfacher Implementierung zu finden, ist abhängig vom jeweiligen Anwendungsfall.
Für Entwickler, Forscher und Anwender empfiehlt es sich, zunächst die Anforderungen an die Punktverteilung genau zu analysieren. Handelt es sich um reine Zufallspunkte mit statistisch korrekter Gleichverteilung, so genügt meist die Transformation der Breitengrade mittels der cos⁻¹-Formel. Benötigt man hingegen eine ästhetisch ansprechende und gleichmäßige Verteilung mit Mindestabständen, sind fortgeschrittene Techniken wie Poisson-Disc-Sampling zu bevorzugen. Abschließend sei erwähnt, dass es zahlreich verfügbare Softwarebibliotheken und Werkzeuge gibt, die diese Verteilungsverfahren bereits implementieren und die serielle oder parallele Generierung von beliebig vielen Punkten auf Kugeln und anderen Oberflächen ermöglichen. Dabei gilt stets, die gewählte Methode hinterfragt und an die jeweils speziellen Anforderungen angepasst wird, um optimale Ergebnisse zu erzielen.
Die Erzeugung von zufälligen, gut verteilten Punkten auf einer Kugel gehört also zu den praxisrelevanten und zugleich faszinierenden Problemen in mathematisch-physikalischer Geometrie und Computergrafik, deren Lösungen eine Brücke zwischen Theorie und praktischen Anwendungen schlagen.