Thermodynamische Computersysteme: Die Revolution für KI-Anwendungen der Zukunft

Die rasante Entwicklung künstlicher Intelligenz (KI) führt immer wieder zu neuen Herausforderungen, insbesondere in Bezug auf die Leistungsfähigkeit und Effizienz von Rechenhardware. Während digitale Computer bislang die Grundlage für KI-Algorithmen bilden, stößt diese traditionelle Hardware zunehmend an physikalische und technische Grenzen. Energieverbrauch und erforderliche Rechenzeiten nehmen rapide zu, was die Skalierbarkeit und Umweltfreundlichkeit moderner KI-Anwendungen einschränkt. Vor diesem Hintergrund gewinnt ein innovatives Konzept immer stärker an Bedeutung: thermodynamische Computersysteme, die neue Wege im Bereich der KI-Berechnung eröffnen können. Thermodynamische Computer basieren auf den Prinzipien der Thermodynamik und der stochastischen Dynamik physikalischer Systeme.

Statt klassischer digitaler Rechenoperationen werden dabei analoge physikalische Prozesse ausgenutzt, um komplexe mathematische Probleme zu lösen. Insbesondere anwendungsnahe KI-Aufgaben wie probabilistisches Denken, Unsicherheitsquantifizierung und generative Modelle profitieren von genau dieser Art von Berechnung, denn die Mathematik hinter probabilistischer KI spiegelt natürliche thermodynamische Verteilungen wider. In einfachen Worten hilft ein thermodynamischer Computer, Formen von Zufall und Rauschen als nützliche Rechenressource zu verwenden. Dies steht im Gegensatz zu digitaler Hardware, bei der zufällige Fehler möglichst vermieden werden müssen. Thermodynamische Systeme leben von Fluktuationen und können dadurch natürliche Wahrscheinlichkeitsverteilungen erzeugen, was für KI-Prozesse von großem Vorteil ist.

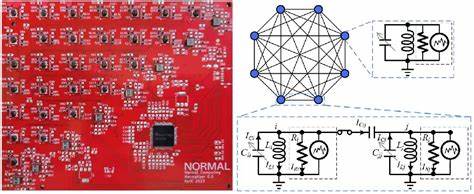
Ein bemerkenswertes Beispiel hierfür ist das sogenannte Stochastic Processing Unit (SPU), eine experimentelle thermodynamische Recheneinheit bestehend aus miteinander gekoppelten elektrischen Schwingkreisen. Diese Einheit simuliert Langevin-Dynamiken, die eine stochastische Differentialgleichung beschreiben, und erlaubt so das Sampling von Wahrscheinlichkeitsverteilungen wie der mehrdimensionalen Gaußverteilung. Die Fähigkeit, solche Verteilungen physikalisch direkt zu erzeugen, stellt für KI-Anwendungen einen enormen Vorteil dar, denn Sampling und unsichere Modellierungsprozesse sind zentraler Bestandteil vieler moderner KI-Algorithmen. Neben Sampling-Aufgaben kann ein thermodynamisches System, wie etwa das SPU, auch effizient komplexe lineare Algebra-Rechenoperationen durchführen. Zum Beispiel ist die Matrixinversion ein fundamentaler Schritt in vielen KI-Methoden, von der Regression bis hin zu fortgeschrittenen Gaussian-Process-Modellen.

Das SPU zeichnet sich dadurch aus, dass es die Inversion positiver semidefiniter Matrizen durch Auswertung der kovarianten Spannungen an den Bauteilen physikalisch realisiert – eine ganz neue Herangehensweise im Vergleich zu den rein algorithmischen digitalen Lösungen. Die experimentellen Resultate zeigen, dass mit der aktuellen Hardware nicht nur der korrekte Mittelwert der gesampelten Verteilungen erreicht wird, sondern auch fortgeschrittene Merkmale wie Kovarianz, Schiefe und Kurtosis genau approximiert werden können. Die Architektur aus RLC-Schwingkreisen ermöglicht es zudem, beliebige Kopplungsstärken programmierbar zu machen, sodass vielseitige Verteilungen entstehen. Die Skalierbarkeit ist jedoch eine Herausforderung, da insbesondere die Verwendung von Induktoren und Transformatoren in der Miniaturisierung und in der Integration auf einem Chip limitierend ist. Um den Weg zu einer breit einsetzbaren thermodynamischen Computerhardware zu ebnen, wurde eine alternative Architektur mit RC-Einheiten und resistiver Kopplung vorgeschlagen.

Diese Architektur vermeidet große Induktivitäten und Transformers, die schwer in integriertem Schaltkreis-Design zu realisieren sind, und ist daher besser für CMOS-Elektronik geeignet. Simulationen mit realistischen Bauteilen und Fertigungsmodellen bestätigen, dass diese Architektur eine ähnliche Leistungsfähigkeit und Genauigkeit erreichen kann wie die ursprüngliche SPU-Variante und trotzdem auf Großserienfertigung ausgerichtet ist. Der entscheidende Vorteil thermodynamischer Algorithmen liegt in ihrer potenziellen Laufzeit- und Energieeffizienz. Modellrechnungen zeigen, dass bei ausreichend großen Systemdimensionen, insbesondere ab etwa 3000 Größenordnung, thermodynamische Systeme digitale GPUs bei der Erzeugung von vielen Zufallsproben oder bei Matrixinversionen deutlich übertreffen können. Dabei sind neben der reinen Rechenzeit auch der Energieverbrauch und die Skalierbarkeit wichtige Faktoren, denn moderne GPUs verbrauchen immense Mengen an Energie, was heute als limitierender Faktor vieler KI-Systeme erkannt wird.

Thermodynamische Computer profitieren davon, dass die physikalischen Fluktuationen selbst optimal für die Sampling-Aufgaben geeignet sind, anstatt als störende Effekte behandelt werden zu müssen. Die natürliche thermische Bewegung und die damit verbundenen Fluktuationen erzeugen dabei automatisch Variabilität, die dem Algorithmus zugutekommt. Gleichzeitig ermöglicht die kapazitive oder resistive Kopplung der Einheiten eine simple und energetisch effiziente Steuerung der Verteilungsparameter. Neben der Skalierung und der Integrationsherausforderungen ist die Präzision der physikalischen Parameter eine wichtige Überlegung. Ungenauigkeiten in den Bauteilen, vor allem im Bereich der Kapazitäten oder Widerstände, können die Qualität des Samples und die Genauigkeit bei linearen Algebra-Aufgaben beeinflussen.

Aktuelle Forschungen zeigen jedoch, dass durch clevere Fehler-Mitigationsstrategien und averaging-basierte Verfahren die Effekte dieser Ungenauigkeiten deutlich reduziert werden können. Dies macht thermodynamische Computerrobust gegenüber gewissen Fertigungstoleranzen und macht sie praktikabel für reale Anwendungen. Ein weiterer Bereich mit großem Potenzial ist die Anwendung thermodynamischer Computer auf nicht-Gaußsche Verteilungen. Während die bislang realisierten Geräte hauptsächlich multivariate Normalverteilungen und zugehörige lineare Operationen unterstützen, können zukünftige Architekturen auch nichtlineare Kopplungen implementieren, um komplexere, nichtlineare Wahrscheinlichkeitsmodelle abzubilden. Dies öffnet den Weg für die Hardwarebeschleunigung generativer Modelle wie Diffusionsmodelle, welche in der modernen KI eine Schlüsselrolle spielen.

Ausblickend betrachtet ist das Feld thermodynamischer Computer vergleichbar mit den frühen Tagen der Quantencomputerentwicklung, mit dem Unterschied, dass thermodynamische Technologien keine extremen Umweltbedingungen wie Kryogenik oder isolierte Quantenbits benötigen. Dies macht sie zu einer vielversprechenden und erreichbaren Alternative für AI-Anwendungen mit hohem Ressourceneinsatz auf vergleichsweise kurze Sicht. Durch ihre Fähigkeit, probabilistische KI, Unsicherheitsquantifizierung und komplexe lineare Algebra-Aufgaben effizienter und energiesparender zu lösen, könnten thermodynamische Computersysteme große Auswirkungen auf Hochleistungs-KI-Systeme haben. Insbesondere in sicherheitskritischen Anwendungen, bei denen verlässliche Unsicherheitsabschätzungen nötig sind, stellen sie einen potenziellen Durchbruch dar. Die Kombination aus physikalischem Rechnen und fortschrittlichen Algorithmen verspricht eine neue Ära der KI-Hardware, die heutigen digitalen Computern überlegen ist und ökologische Vorteile mit sich bringt.

Zusammenfassend ist die Entwicklung thermodynamischer Computersysteme ein spannendendes Forschungsgebiet mit hochgradigem Potenzial. Von Konzepten wie dem SPU bis hin zu skalierbaren chipintegrierten Architekturen mit resistiver Kopplung zeigen sich vielfältige Möglichkeiten, KI-Rechenoperationen effizienter, schneller und mit geringerem Energieverbrauch durchzuführen. Herausforderungen hinsichtlich der Bauteilpräzision und der Vernetzung großer Einheiten sind lösbar und werden aktiv erforscht. Somit steht thermodynamisches Computing kurz davor, die künstliche Intelligenz nachhaltiger und leistungsfähiger zu machen – ein wichtiger Schritt für die Zukunft wichtiger KI-Anwendungen in Wissenschaft, Wirtschaft und Gesellschaft.