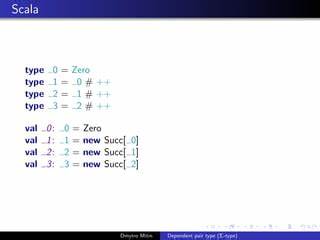
In der heutigen Welt von Softwareentwicklung und mathematischer Beweisführung gewinnt die formale Verifikation zunehmend an Bedeutung. Besonders bei komplexen Algorithmen, wie der dynamischen Programmierung, ist die Gewährleistung von Korrektheit entscheidend. Lean, ein modernes interaktives Theorembeweissystem, bietet mit seinem ausdrucksstarken Typensystem und der Unterstützung für abhängige Typen eine Plattform, auf der verifizierte Algorithmen elegant formuliert und bewiesen werden können. Ein wesentlicher Bestandteil dieser Arbeit sind Σ-Typen (Sigma-Typen), die es ermöglichen, Werte mit komplexen Abhängigkeiten und Beweisobjekten zusammenzuführen. Der folgende Beitrag erläutert ausführlich, wie durch die Kombination von dynamischer Programmierung und Σ-Typen in Lean verifizierte, sichere und nachvollziehbare Algorithmen erstellt werden können.
Dabei wird auch auf die Vorteile gegenüber herkömmlichen Ansätzen eingegangen und die praktischen Anwendungen werden vorgestellt. Die dynamische Programmierung ist eine algorithmische Technik zur effizienten Lösung von Optimierungsproblemen, die sich durch überlappende Teilprobleme und optimale Teilstruktur auszeichnen. Klassischerweise wird sie oft in imperativen Sprachen implementiert, wobei sich bei komplexeren Problemen die Korrektheit der Umsetzung schwer nachweisen lässt. Durch die Verwendung von Lean und insbesondere Σ-Typen kann jede Zwischenlösung nicht nur als Wert, sondern gleichzeitig als Beleg für deren Korrektheit angegeben werden. Dies sorgt für ein Höchstmaß an Sicherheit und Transparenz in komplexen Systemen.
Σ-Typen ermöglichen die Verbindung eines Datenelements mit einem Beweisobjekt, das eine Eigenschaft über diesen Wert garantiert. In Lean lassen sich somit beispielsweise Teilergebnisse eines dynamischen Programmierproblems nicht nur speichern, sondern auch deren korrekte Berechnung formal beweisen. Das reduziert das Risiko, Fehlannahmen zu treffen oder Berechnungsschritte falsch zu interpretieren. Diese Technologie erlaubt es, die Algorithmen als vollständige mathematische Objekte zu begreifen, welche nicht nur Berechnungen durchführen, sondern gleichzeitig Beweise für Aussagen erzeugen. Die Implementierung von dynamischer Programmierung mit Σ-Typen in Lean erfordert ein Umdenken gegenüber traditionellen Programmierparadigmen.
Während Imperativsprachen Wert auf schnelle Implementierung legen, lautet das Ziel hier die absolute Verifizierung. Flexible Typkonstrukte von Lean helfen dabei, komplexe Induktionsbeweise und Korrektheitsargumente direkt in den Programmcode zu integrieren. Dadurch wechseln Programmierer vom Debuggen unübersichtlicher Logik zu einem Prozess, bei dem jede Funktionserklärung mathematisch sauber abgesichert wird. Ein häufig genutztes Beispiel für verifizierte dynamische Programmierung ist die Berechnung der längsten gemeinsamen Teilfolge (Longest Common Subsequence, LCS). Bei traditionellen Implementierungen sind Randfälle und Indizierungsfehler nicht selten.
In Lean kann das LCS-Problem so formuliert werden, dass neben dem Ergebnis zugleich bewiesen wird, dass keine längere gemeinsame Teilfolge existiert und die Lösung somit optimal ist. Die Verwendung von Σ-Typen bindet die Ergebnisse unmittelbar an Beweise, was die Korrektheit nachweislich sichert. Neben der Korrekheitssicherung bietet die Lean-basierte Dynamische Programmierung mit Σ-Typen auch Vorteile in der Modularität und Wartbarkeit von Code. Das starke Typensystem erzwingt explizite Spezifikationen der Funktionen und deren Voraussetzungen. Das erhöht die Verständlichkeit und erleichtert spätere Erweiterungen oder Anpassungen.
Die Softwareentwicklung nähert sich hier einer mathematischen Disziplin an, in der jeder Schritt transparent und formal nachvollziehbar ist. Der Lernaufwand für das Entwickeln von Programmen in Lean ist zwar höher als bei vielen konventionellen Programmiersprachen, doch die Belohnung liegt in nachvollziehbaren und formalen Sicherheitsgarantien. Für sicherheitskritische Bereiche wie Kryptografie, Verifikationssoftware und komplexe mathematische Modellierungen ist der Einsatz von Lean und Σ-Typen bei dynamischer Programmierung daher äußerst attraktiv. In diesen Feldern können Fehler gravierende Folgen haben, die ein bewährtes System wie Lean effektiv minimiert. In der Praxis zeigen aktuelle Projekte, dass die Kombination von dynamischer Programmierung und Σ-Typen in Lean auch bessere Wartungsfähigkeit bei komplexen Algorithmusverbesserungen ermöglicht.
Durch die klare Typisierung kann der Programmierer Funktionsteile gezielt ersetzen oder erweitern, während die formalen Beweise automatisch angepasst oder abgerufen werden. Das bedeutet, dass der Code robust gegenüber Änderungen bleibt, was in der Softwareentwicklung ein sehr wertvoller Faktor ist. Neben der Verwendung von Lean gibt es auch andere proof assistants wie Coq oder Agda, die ähnliche Prinzipien verfolgen. Doch Lean zeichnet sich durch einen sehr modernen, nutzerfreundlichen Ansatz und eine aktive Community aus, die Werkzeuge und Bibliotheken im dynamischen Programmierungskontext stetig ausbauen. Gerade die Unterstützung von Σ-Typen bietet hier einen deutlichen Vorteil, da das Zusammenspiel von Wert und Beweis elegant abgebildet bleiben kann.
Ein zentrales Element für die Akzeptanz der Methode bleibt jedoch die Zugänglichkeit der Lernmaterialien und eine aktive Community, die Anwendungsfälle und Best Practices teilt. Je mehr Entwickler und Mathematiker Dynamische Programmierung mit Σ-Typen in Lean erlernen, desto breiter kann sich diese verifizierte Methode etablieren. Durch offene Quellen und zugängliche Tutorials wird eine kontinuierliche Vergrößerung der Anwenderbasis ermöglicht. Abschließend lässt sich festhalten, dass Verified Dynamic Programming mithilfe von Σ-Typen in Lean den Weg zu wirklich robusten, nachvollziehbaren und mathematisch verifizierten Algorithmen ebnet. Diese Technologie steht am Schnittpunkt moderner Softwareentwicklung und theoretischer Mathematik, wodurch sie sowohl in der Forschung als auch in industriellen Anwendungen zunehmend an Bedeutung gewinnt.
Die Investition in das Verständnis und die Implementierung dieser Methoden zahlt sich in Form von Qualität, Sicherheit und Zukunftsfähigkeit von Softwareprojekten doppelt aus. Die Dynamische Programmierung erhält so einen sicheren und formalen Rahmen, der weit über herkömmliche Implementationen hinausgeht und neue Maßstäbe in der Verifikation setzt.