Quantencomputing ist längst nicht mehr nur ein theoretisches Konzept, sondern avanciert zunehmend zu einer praxisnahen Technologie, die die Art und Weise, wie wir komplexe Probleme lösen, maßgeblich verändern könnte. Für Einsteiger in diesen Bereich sind die Prinzipien hinter den Quantenalgorithmen und deren Implementierung von großer Bedeutung, um die Potenziale und Herausforderungen zu verstehen, die mit Quantencomputern einhergehen. In den letzten Jahren haben IBM und weitere Anbieter die Möglichkeit geschaffen, reale Quantenprozessoren über cloudbasierte Plattformen zugänglich zu machen, wodurch gerade auch Entwickler und Forscher außerhalb der theoretischen Physik erste praktische Erfahrungen sammeln können. Die Grundlage des Quantencomputings ist das Qubit, die kleinste Informationseinheit, die durch Quantensuperposition weit mehr Rechenkapazität bietet als klassische Bits. Qubits können sich in den Zuständen 0, 1 oder in einer überlagerten Kombination beider befinden, was durch komplexe mathematische Vektoren im sogenannten Hilbertraum beschrieben wird.
Wichtige Konzepte wie Verschränkung und Quantenoperationen, die mit unitären Matrizen abgebildet werden, machen die Besonderheit der Quantenprogrammierung aus. Während klassisches Rechnen klar diskrete Zustände verarbeitet, erlaubt Quantencomputing dank Superposition und Interferenz Verfahren, die gewisse Aufgaben exponentiell oder quadratisch schneller lösen können. Dabei sind die Einheiten des Quantencomputers, sogenannte Quantenoperationen oder Gates, von der Natur her reversibel und lassen sich am besten mit einer Kombination aus einfachen Ein-Qubit- und Zwei-Qubit-Gattern darstellen. IBM Quantum Experience stellt ein Gate-Set bereit, das unter anderem Hadamard-, Pauli- und CNOT-Gatter umfasst, die für die Erstellung und Manipulation von Quantenstates essentiell sind. Diese Operationen werden in Form von Quanten-Schaltkreisen visualisiert, in denen die Zeitachse von links nach rechts verläuft, und Reihen horizontal die einzelnen Qubits zeigen.
Durch die Verbindung von Gates auf den entsprechenden Qubits lassen sich komplexe Algorithmen abbilden und auf der Hardware umgesetzt werden. Für die Programmierung dieser Quantenalgorithmen hat sich Qiskit etabliert. Als Python-basierte Open-Source-Software erlaubt es Qiskit, sowohl auf Simulatoren als auch auf echten IBM Quantencomputern zu arbeiten. Die Entwicklung im Software-Stack umfasst Module für das Design der Schaltkreise, die Ausführung, Simulation und Fehlerkorrektur. Dabei ist das Erlernen von Qiskit für Einsteiger essenziell, da es die Tür zu komplexeren Algorithmen und tiefgreifender Analysen öffnet.
Ein typisches Programm besteht aus Schaltkreis-Design und anschließender Ausführung auf einem ausgewählten Backend, wobei durch Messungen das Ergebnis klassisch ausgewertet wird. In der Praxis sind Quantencomputeralgorithmen nach Problembereichen differenziert – so finden sich Anwendungen in Bereichen wie Graphentheorie, Zahlentheorie oder maschinelles Lernen. Zu den prominentesten Algorithmen zählt Grovers Suchalgorithmus, der eine quadratische Beschleunigung beim Durchsuchen unsortierter Datenbanken ermöglicht. Seine Implementierung auf 5-Qubit-Computern wie ibmqx4 verdeutlicht die Übersetzung theoretischer Prinzipien in hardwaretaugliche Schaltkreise, bei denen Toffoli-Gatter (dreiqubitige Logikgatter) und Diffusionsoperatoren die Schlüsselkomponenten bilden. Der Bernstein-Vazirani-Algorithmus etwa zeigt eindrucksvoll, wie ein Programm in nur einem einzigen Aufruf eine versteckte Bitfolge ermittelt – während klassisch dessen Aufwand linear zur Anzahl der Bits wäre.
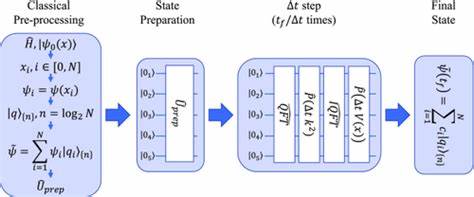
Dabei wird die Komplexität der Orakel-Implementierung deutlich, die häufig den Engpass in der praktischen Anwendung darstellt. Die automatische Kompilierung komplexer Matrizen in ausführbare Quanten-„Netzlisten“ mittels spezialisierter Software erleichtert hier den Einstieg erheblich. Ein weiteres bedeutendes Beispiel ist Shors Algorithmus zur Faktorisierung großer Zahlen, der zwar auf aktuellen Geräten aufgrund des qubitbezogenen und gatebezogenen Ressourcenbedarfs technisch herausfordernd ist, aber als Meilenstein für die zukünftige Kryptographie gilt. Die Reduktion der Faktorisierung auf das Finden der Periode eines modularen Exponentialfunktion zeigt, wie klassische Probleme elegant mit Quantentechniken kombiniert werden können. Auch die quantenmechanische Simulation vieler Systeme, wie etwa der Lösung der Schrödingergleichung, profitiert von den Vorteilen der Quantencomputer.
Hier werden Unitaries wie der Quantum Fourier Transform verwendet, um zeitliche Entwicklungen von Wellenfunktionen abbilden zu können. Trotz der engen Ressourcen der verfügbaren 5-Qubit-Systeme erlauben kleinere Simulationen bereits erste Einblicke. Varianten der Variational Quantum Eigenevalue Solver (VQES) nutzen hybride Ansätze, bei denen klassische Optimierer Parameter für quantenmechanische Schaltkreise bestimmen, um beispielsweise den Grundzustand des Transversalen Isingmodells zu approximieren. Dies erlaubt zumindest auf kleinen Systemen und mit geringen Qubitanzahlen eine praktikable Annäherung, die für viele physikalische Systeme relevant ist. Im maschinellen Lernen finden sich Konzepte wie Quantum Principal Component Analysis (QPCA) und Quanten-Support-Vektor-Maschinen, die komplexe Datenstrukturen mit quantenbasierten Algorithmen effizienter analysieren könnten.
Leider sind praktische Implementierungen gegenwärtig meist lediglich im frühen Forschungsstadium auf Simulatoren realisierbar. Quantenfehlerkorrektur stellt eine der größten Herausforderungen dar. Trotz der Nutzung von Repetition- und anderen Codes auf kleinen Quantencomputern zeigt sich, dass Fehlerquellen durch Gate-Fehlerraten und Zusammenwirken komplexer Korrekturschemata häufig nicht exponentiell reduziert werden. Dadurch ist der praktische Nutzen klassischer Korrekturcodes noch begrenzt. Testreihen auf IBM Quantenhardware verdeutlichen, dass bei leicht zugänglicher Hardware bislang die Fehlerbehebung auf kleiner Skala zwar erste Erfolge bringt, aber der Skalierung zu größeren und komplexeren Systemen im Weg steht.
Zusammenfassend bieten heutige Quantencomputer einen spannenden Zugang zu grundlegenden Quantenalgorithmen und ermöglichen erste experimentelle Umsetzungen wichtiger Verfahren aus den Bereichen Suche, Lineare Algebra, Zahlentheorie und Simulation. Der Einstieg in die Quantenprogrammierung erfordert aber weiterhin ein solides Verständnis der zugrunde liegenden Mathematik und Physik, verbunden mit der Kenntnis von verfügbaren Hardware-Restriktionen und Software-Frameworks wie Qiskit. Schritt für Schritt eröffnen sich so in der Praxis bisher verborgene Möglichkeiten und konkrete Anwendungen. Das Experimentieren mit existierender Hardware ist heute die wahrscheinlich beste Gelegenheit für Entwickler, Chancen und Limitationen kennenzulernen, die Quantencomputing mit sich bringt. Parallel dazu treiben Weiterentwicklungen der Hardware und verschiedener Quantenparadigmen die Technologie voran, um bald reale Vorteile, wie das schnelleres Lösen klassisch schwerer Probleme, zu ermöglichen.
So bildet die Auseinandersetzung mit Quantenalgorithmusimplementierungen einen zentralen Baustein für den Aufbau eines tiefgreifenden Verständnisses im schnell wachsenden Feld der Quanteninformationstechnologie.