In der Welt des maschinellen Lernens und der statistischen Modellierung begegnet man häufig Begriffen wie Lernkurven und Overfitting, welche eng miteinander verbunden, aber oft missverstanden werden. Besonders in wissenschaftlichen Kreisen und der Praxis verbreitet sich der Irrglaube, dass eine große Differenz zwischen Trainings- und Testleistung eines Modells automatisch auf Overfitting hindeutet. Dieses Missverständnis tritt auch in Vorlesungen, Blogbeiträgen und sogar in Fachpublikationen auf und führt nicht selten zu falschen Schlussfolgerungen und Fehlinterpretationen bei der Modellbewertung. Um diese Verwirrung zu klären, ist es essenziell, zwischen Lernkurven und so genannten Occam-Kurven zu differenzieren. Diese Trennung hilft, Overfitting auf korrekte Weise zu identifizieren und die Generalisierungsfähigkeit von Modellen besser zu verstehen.
Lernkurven sind ein klassisches Werkzeug, um den Lernfortschritt eines Modells in Bezug auf seine Leistung im Laufe der Zeit oder über wachsendes Erfahrungsmaterial darzustellen. Der Begriff geht zurück auf die Untersuchungen von Ebbinghaus zur menschlichen Erinnerung und wurde auf maschinelles Lernen übertragen. Konkret zeigen Lernkurven die Beziehung zwischen der Menge an Trainingsdaten und der Leistung eines einzelnen Modells, typischerweise gemessen an Trainings- sowie Validierungs- oder Testfehlern. Eine optimale Lernkurve sollte monoton steigend sein und damit signalisieren, dass das Modell mit zunehmenden Datenmengen lernt und besser generalisiert. Die Differenz zwischen der Trainings- und Testleistung eines Modells wird als Generalisierungslücke bezeichnet.
In vielen Fällen ist diese Lücke ein Maß dafür, wie gut ein Modell tatsächlich auf unbekannte Daten übertragbar ist. Ein hoher Generalisierungslücke wird oft mit Overfitting assoziiert, also mit einem Zustand, in dem ein Modell zu stark auf die Trainingsdaten angepasst ist und dadurch auf neuen Daten schlechter performt. Doch dieser Zusammenhang ist nicht so einfach und direkt, wie vielfach angenommen. Ein zentrales Problem ist, dass die Generalisierungslücke allein noch keine eindeutige Aussage über Overfitting ermöglicht. Overfitting ist vielmehr ein Problem der Modellkomplexität und der Vergleichbarkeit zwischen verschiedenen Modellen.
Es stellt sich die Frage, wie sehr ein Modell von einem anderen Modell abweicht und ob diese Abweichung auf unnötige Komplexität zurückzuführen ist. Genau an dieser Stelle kommen die Occam-Kurven ins Spiel. Sie bieten eine konzeptuelle und mathematische Grundlage, um das komplexitätsbezogene Verhalten von Modellen zu beurteilen. Occam-Kurven sind benannt nach dem Prinzip von Occam's Razor, dem Sparsamkeitsprinzip in der wissenschaftlichen Erkenntnis, das besagt, dass die einfachste Erklärung in der Regel bevorzugt werden sollte. Im Kontext des maschinellen Lernens stehen Occam-Kurven für eine Darstellung der Modellleistung über verschiedene Modelle hinweg, geordnet nach einem Komplexitätsmaß.
Anders als Lernkurven, die sich auf einen einzelnen Modelltyp mit variierender Datenmenge fokussieren, vergleichen Occam-Kurven verschiedene Modelle mit jeweils unterschiedlicher Komplexität über wachsende Datengrößen. Die Herstellung einer Occam-Kurve erfordert die Definition eines konkreten Komplexitätsmaßes, welches die strukturelle oder statistische Komplexität eines Modells quantifiziert. Dies kann beispielsweise anhand der Anzahl der Parameter, der Tiefe eines neuronalen Netzes oder anderer komplexitätsbezogener Kennzahlen geschehen. Im Zusammenspiel mit der Größe des Trainingsdatensatzes entsteht eine zweidimensionale Kurve, die die Performance im Hinblick auf diese beiden Variablen abbildet. Der entscheidende Unterschied zwischen Lernkurven und Occam-Kurven liegt in ihrer Aussagekraft für Overfitting.
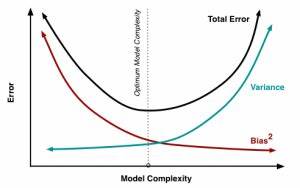
Während Lernkurven nur das Lernen eines einzelnen Modells betrachten und somit hauptsächlich die Generalisierungsfähigkeit im Zeitverlauf illustrieren, ermöglichen Occam-Kurven eine gezielte Analyse der Bias-Variance-Tradeoff und eine detaillierte Beurteilung der Modellkomplexität. Overfitting wird in diesem Rahmen als eine Lücke in der Performancedarstellung zwischen Modellen verschiedener Komplexität sichtbar, was als Occam’s Gap bezeichnet wird. Die Konsequenz daraus ist, dass allein anhand von Lernkurven und der Generalisierungslücke keine verlässliche Diagnose über Overfitting gezogen werden kann. Stattdessen muss man eine vergleichende Analyse vornehmen, bei der verschiedene Modelle oder inductive biases hinsichtlich ihrer Komplexität und Leistung miteinander verglichen werden. Nur so kann entschieden werden, ob ein Modell unnötig komplex ist und dadurch seine Fähigkeit zur Generalisierung verschlechtert.
Verständnis für dieses Konzept ist insbesondere im Zeitalter von Deep Learning und komplexen Modellsystemen unabdingbar. In der Praxis ist es keine Seltenheit, dass komplexe Modelle mit viel parametrischer Freiheit auch große Differenzen zwischen Trainings- und Testfehler zeigen. Dennoch kann ein solches Modell durchaus optimal generalisieren, wenn es im Vergleich zu einfacheren Modellen eine bessere Performance erreicht oder sich in einem günstigen Bereich der Occam-Kurve befindet. Umgekehrt können Modelle mit vermeintlich kleinen Generalisierungslücken dennoch materielle Verfehlungen im Sinne von Overfitting beinhalten, wenn sie im Vergleich zur Komplexitäten-Skala unnötig aufwändig sind und dadurch anfälliger für Rauschen. Die Relevanz der Occam-Kurven geht über das reine Verstehen des Overfitting-Problems hinaus.
Sie etablieren ein Werkzeug, um den Prozess der Modellselektion besser zu gestalten und die Bias-Variance-Dynamik quantitativ sichtbar zu machen. Weiterhin bieten sie Ansatzpunkte, um das Phänomen des sogenannten Double Descent zu interpretieren, bei dem die Testfehlerkurve bei wachsender Modellkomplexität nicht monoton steigt, sondern zunächst zunehmendes Overfitting zeigt, dann aber wider Erwarten wieder bessere Generalisierung demonstriert. Dieses Verhalten ist mit klassischem Verständnis von Lernkurven schwer zu interpretieren, lässt sich mit Occam-Kurven jedoch anschaulicher erklären. Für Praktiker im Bereich Data Science und maschinelles Lernen bedeutet das vor allem eine Verschiebung in der Herangehensweise an die Modellauswahl und Fehlerbewertung. Statt sich auf einfache Trainings- und Validierungsfehlerdifferenzen zu verlassen, lohnt es sich, verschiedene Modelle mit unterschiedlichen Komplexitäten zu trainieren und deren Leistungsverläufe über Datenmengen zu beobachten.
So lassen sich fundierte Entscheidungen treffen, welches Modell tatsächlich die beste Balance aus Bias und Varianz (Systematik und Flexibilität) bietet. Zusammenfassend lässt sich sagen, dass die vermeintlich intuitive Methode, Overfitting anhand der Generalisierungslücke in Lernkurven zu beurteilen, den Kern des Problems verfehlt. Overfitting ist vielmehr ein relatives Konzept, das nur im Vergleich unterschiedlicher Modelle mit variierender Komplexität sinnvoll bewertet werden kann. Occam-Kurven bieten hier die notwendige konzeptuelle und methodische Grundlage, um den Bias-Variance-Tradeoff und den Einfluss der Modellkomplexität auf die Generalisierungsfähigkeit gezielt zu untersuchen. Die Erkenntnisse zu Lern- und Occam-Kurven tragen nicht nur zu einer genaueren Diagnose von Overfitting bei, sondern fördern auch die Entwicklung besser interpretierbarer und robusterer Modelle im maschinellen Lernen.
Dies ist ein Schritt hin zu einem tieferen Verständnis der Modellbildung und dem verantwortungsvollen Einsatz komplexer lernender Algorithmen in Wissenschaft und Industrie. Schließlich zeigt sich, dass die richtige Differenzierung und Nutzung dieser Kurven essenziell für den Fortschritt in der Modellbewertung ist und Fehldeutungen nachhaltig vermeidet.