Die Verarbeitung von Sprachsignalen ist eine komplexe, aber zugleich faszinierende Aufgabe, die eine zentrale Rolle in vielen Anwendungen des maschinellen Lernens spielt. Ob automatische Spracherkennung, Sprecheridentifikation oder andere sprachbasierte Systeme – die Art und Weise, wie Sprachdaten aufbereitet und interpretiert werden, beeinflusst maßgeblich die Leistungsfähigkeit der Modelle. Zwei der wichtigsten Konzepte in der Sprachverarbeitung sind Filterbänke und Mel-Frequenz-Cepstralkoeffizienten, kurz MFCCs. Beide Ansätze dienen dazu, aus rohen Audiowellenformen repräsentative Merkmale herauszufiltern, die von maschinellen Lernalgorithmen weiterverarbeitet werden können. Nachfolgend wird ausführlich analysiert, was Filterbänke und MFCCs genau sind, wie sie berechnet werden und weshalb sich in jüngerer Zeit ein Trend hin zu Filterbänken als bevorzugten Merkmalen abzeichnet.
Die Grundlage jeder Verarbeitung von Sprachsignalen beginnt mit einer Vorverarbeitung des Rohsignals, das als zeitabhängige Amplitudenwelle vorliegt. Dieses Signal wird zunächst durch einen sogenannten Pre-Emphasis-Filter geleitet. Ziel dieses Filters ist es, die hohen Frequenzanteile des Signals zu verstärken, da diese in natürlicher Sprache oft eine geringere Amplitude aufweisen als niederfrequente Bestandteile. Dieser Filter gleicht somit die Frequenzverteilung aus und sorgt darüber hinaus dafür, dass spätere Rechenschritte, insbesondere die Fourier-Transformation, stabiler und numerisch robuster ablaufen. Die typischen Filterkoeffizienten liegen in einem Bereich von etwa 0,95 bis 0,97.
Obwohl moderne Fast-Fourier-Transform-Implementierungen mittlerweile recht stabil sind, verbessert der Pre-Emphasis-Filter weiterhin die Signalqualität und signalisiert dem Modell relevante Informationen, die andernfalls leicht verloren gehen könnten. Nach der Voranhebung der höheren Frequenzen wird das Signal in kurze Abschnitte, sogenannte Frames, unterteilt. Dies ist entscheidend, da Sprache ein hochdynamisches Signal ist, dessen Frequenzinhalt sich ständig ändert. Eine Fourier-Transformation des gesamten Signals würde wichtige zeitliche Veränderungen verwischen und zu einer ungenauen Repräsentation führen. Um dies zu vermeiden, werden typischerweise Frames von etwa 20 bis 40 Millisekunden Länge mit Überlappungen von etwa 50 Prozent gewählt.
Diese kurzen Abschnitte erlauben es, die Frequenzzusammensetzung lokaler Abschnitte genauer zu analysieren und beinhalten gleichzeitig genug Daten, um aussagekräftige Merkmale zu extrahieren. Bevor die Fourier-Transformation auf jedes Frame angewendet wird, erfolgt die Multiplikation mit einem Fensterfunktion, meist einem Hamming-Fenster. Diese Praxis mindert das sogenannte Spektralleckage-Problem, das durch die Annahme der Fourier-Transformation entsteht, das Signal sei unendlich periodisch. Das Hamming-Fenster sorgt dafür, dass die Ränder der Frames sanft abklingen und verhindert dadurch unnatürliche Sprünge, die zu Verzerrungen im Frequenzspektrum führen könnten. Mit der Anwendung der Short-Time Fourier Transform (STFT) auf jedes einzelne Frame wird das zeitlich begrenzte Frequenzspektrum ermittelt.
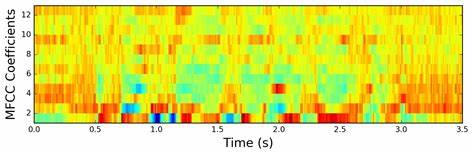
Dabei entstehen komplexe Spektralwerte, aus denen mit der Berechnung des Betragsquadrats die Leistungsspektren oder Periodogramme entstehen. Diese Spektren bilden die Basis für die weitere Verarbeitung mit Filterbänken. Filterbänke sind eine Sammlung von Bandpassfiltern, die in der Frequenz so angeordnet sind, dass sie dem menschlichen Hörempfinden ähneln. Statt linearer Frequenz-Skala wird hier die sogenannte Mel-Skala verwendet, die tieferen Frequenzen mit höherer Auflösung und höheren Frequenzen mit geringerer Auflösung abbildet. Dies spiegelt das nicht-lineare Verhalten des menschlichen Gehörs wider.
Typischerweise werden etwa 40 Filterbänder verwendet, die jeweils eine dreieckige Übertragungsfunktion besitzen, welche den Koeffizienten bei der Mitte am höchsten gewichtet und sich zu den Nachbarfiltern hin linear vermindert. Die Anwendung dieser Filterbänke auf das Leistungsspektrum führt zu einer Reduktion der Spektraldaten auf eine kompakte Repräsentation von Energieanteilen in den jeweiligen Frequenzbändern. Ein wichtiger Vorteil der Filterbank-Methodik besteht darin, dass sie die wesentlichen akustischen Merkmale bewahrt und gleichzeitig eine Datenreduktion erreicht. Somit eignen sie sich hervorragend als Features für viele moderne machine-learning-Modelle. Ein zusätzlicher Schritt, der häufig durchgeführt wird und der den Unterschied zu den klassischen MFCC-Features ausmacht, ist die logarithmische Transformation der Filterbankenergien, welche eine bessere Dynamikreduktion und Verzerrungsrobustheit ermöglicht.
MFCCs bauen auf den Filterbänken auf und erweitern die Verarbeitungsschritte um eine diskrete Kosinustransformation (DCT). Durch diese wird eine sogenannte Dekorrelation der Filterbankkoeffizienten erreicht, was vor allem bei älteren maschinellen Lernalgorithmen, beispielsweise Gaussian Mixture Models kombiniert mit Hidden Markov Models (GMM-HMM), von großer Bedeutung war. Die DCT komprimiert die Information, indem sie redundante und hoch korrelierte Datenanteile entfernt und es so ermöglicht, nur die wichtigsten Koeffizienten, meist der Reihenfolge zwei bis dreizehn, zu behalten. Diese Komprimierung unterstützt eine effizientere und stabilere Klassifikation. Im historischen Kontext sind MFCCs das Ergebnis intensiver Forschung bis zur Mitte der 2000er Jahre, als sie zum Standard für Sprachfeatures avancierten, da GMM-HMM-Modelle stark von unkorrelierten und niedrigen Dimensionalitäten profitierten.
Durch die fortschreitende Entwicklung in Deep-Learning-Technologien wird jedoch zunehmend hinterfragt, ob der aufwändige Schritt der Dekorrelation durch die DCT noch notwendig ist. Tiefe neuronale Netze vertragen oft stark korrelierte sowie hochdimensionale Eingaben besser und können durch ihre nichtlineare Verarbeitung sogar von der ursprünglichen, nicht komprimierten Filterbankrepräsentation profitieren. Bei neueren Sprachverarbeitungssystemen ist deshalb ein Trend spürbar, bei dem Filterbank-Features gegenüber den klassischen MFCCs bevorzugt werden. Dabei wird der gesamte Informationsgehalt weitestgehend bewahrt, ohne dass ein möglicher Informationsverlust durch den DCT-Schritt entsteht. Diese Entwicklung reflektiert die Veränderung im methodischen Fokus von traditionellen statistischen Modellen zu datengetriebenen, tiefen Modellen.
Abschließend ist es wichtig, auch die Möglichkeit zu erwähnen, völlig auf Frequenztransformationen, wie die Fourier-Transformation, zu verzichten. Einige aktuellste Ansätze versuchen, direkt aus Rohsignalen im Zeitbereich zu lernen. Diese Methoden erfordern jedoch sehr große Datenmengen und komplexe Modelle, da das Netz mehr Funktionen, inklusive der Frequenzanalyse, selbst erlernen muss. Die inhärente Schwierigkeit der Fourier-Transformation und der zeitlich kurzen Stationaritätserklärungen machen diesen Schritt jedoch traditionell als wichtigen und hilfreichen Bestandteil der Vorverarbeitung weiterhin relevant. Die Wahl zwischen Filterbänken und MFCCs ist daher auch eine Frage der verwendeten Modelle und Anwendungsfälle.