Das maschinelle Lernen befindet sich in einem ständigen Wandel. Ständig werden neue Erkenntnisse gewonnen und Technologien entwickelt, die die Fähigkeiten von Modellen verbessern und zugleich den Trainingsaufwand reduzieren. Eines dieser faszinierenden Phänomene innerhalb der Welt des Deep Learning ist das sogenannte "Grokking". Grokking beschreibt einen überraschenden Lernprozess, bei dem ein Modell trotz anfänglicher scheinbarer Überanpassung an Trainingsdaten plötzlich eine bemerkenswerte Generalisierung erreicht. Nach mehreren Epochen, in denen das Modell zwar auf den Trainingsdaten nahezu perfekte Leistung zeigt, aber auf Validierungsdaten kaum besser als zufällig abschneidet, erlebt es einen plötzlichen Sprung in der Validierungsgenauigkeit.
Dieses unerwartete Verhalten wirft Fragen auf und weckt großes Interesse in Forschung und Praxis. Kürzlich hat sich ein neuartiger Optimierer namens Muon (MomentUm Orthogonalized by Newton-Schulz) als vielversprechende Lösung für eine beschleunigte und stabilere Grokking-Erfahrung erwiesen. Diese Innovation könnte die Art und Weise, wie neuronale Netzwerke trainiert und optimiert werden, nachhaltig verändern. Das Wesen des Grokking-Phänomens beruht auf der Fähigkeit eines Modells, erst nach einem längeren Training eine innere, tiefere Struktur der Daten zu erfassen. Die Bezeichnung Grokking stammt ursprünglich aus der Popkultur und bedeutet, etwas vollkommen zu verstehen oder zu verinnerlichen.
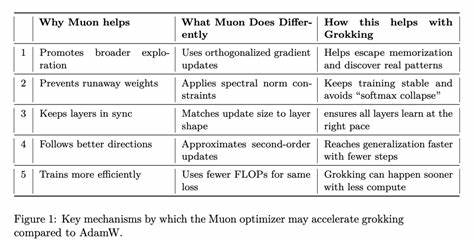
Im Kontext des maschinellen Lernens beschreibt es den Moment, in dem ein Modell plötzlich das zugrunde liegende Muster erfasst, das es zuvor nur oberflächlich zu lernen schien. Dieses plötzliche Verständnis ist von großem Interesse, denn es zeigt, dass manche Modelle auf lange Sicht selbst komplexe Muster finden können – auch wenn sie zu Beginn nicht sofort generalisieren. Die Herausforderung besteht jedoch darin, dass das Erreichen dieses Moments oft einen hohen Trainingsaufwand bedingt. Der Muon-Optimierer wurde genau in diesem Rahmen entwickelt. Im Gegensatz zu weit verbreiteten Optimierern wie AdamW, die hauptsächlich auf adaptiven Lernraten und gewichteten Momenten basieren, setzt Muon auf eine mathematisch ausgeklügelte Strategie: Er kombiniert SGD mit Nesterov-Momentum und führt eine spezielle Orthogonalisierung der Update-Matrizen mithilfe der Newton-Schulz-Iteration durch.
Diese Technik zielt darauf ab, die Struktur der Gradient-Updates so zu gestalten, dass sie im Parameterraum effizienter und stabiler unterwegs sind. Dabei kann der Optimierer gezielt die spektrale Norm der Updates kontrollieren, wodurch Überanpassung und einfache Auswendiglernen vermieden werden sollen. Dadurch werden Modelle sanfter aber sicherer in Richtung echter Muster gelenkt. Ein besonderes Augenmerk lag in der Forschung auf internen Schichten von Modellen mit mehrdimensionalen Gewichtsmatrizen. Muon eignet sich besonders gut für diese Bereiche, wohingegen Komponenten mit ein- oder zweidimensionalen Parametern, wie Embeddings oder Klassifikationsköpfe, derzeit besser mit traditionellen Verfahren wie AdamW trainiert werden.
Diese differenzierte Herangehensweise verdeutlicht, wie facettenreich und spezialisiert Optimierungsprozesse heute betrachtet werden müssen. Die Bedeutung von Muon zeigt sich besonders im Kontext klassischer Herausforderungen für Grokking, beispielsweise bei Aufgaben wie modularer Arithmetik oder der Paritätserkennung von Binärstrings. Diese Probleme sind bewusst gewählt, da sie das Phänomen des Grokkings besonders gut demonstrieren. Forschende setzten verschiedene Softmax-Varianten ein, um die Stabilität der Aktivierungsfunktionen zu testen, da Softmax-Instabilitäten bisher als Einflussfaktor auf Grokking vermutet wurden. Dabei kamen neben dem klassischen Softmax auch Stablemax – eine stückweise lineare Alternative mit besserer Stabilität – sowie Sparsemax, die zu sparsamen Aktivierungen führt, zum Einsatz.
In detailierten Experimenten mit Transformer-Architekturen, die Identitäts-Embeddings, RoPE (Rotary Positional Encoding), RMSNorm und SiLU-Aktivierungen sowie Dropout verwendeten, wurde Muon gegen den AdamW-Optimierer mit gängigen Parametern (Beispielsweise β1=0,9 und β2=0,98) getestet. Die Resultate waren beeindruckend: Muon beschleunigte den Grokking-Prozess signifikant und verkürzte die Zeit bis zum Erreichen einer Validierungsgenauigkeit von 95 % deutlich. Während Modelle mit AdamW oft erst nach etwa 150 Trainingszyklen zu grokken begannen, trat dieser Effekt bei Modellen mit Muon schon um die 100 Epochen auf. Zudem zeigte die Verteilung der Grokking-Zeiten eine geringere Varianz, was auf eine höhere Stabilität und Vorhersagbarkeit des Trainingsverlaufes hindeutet. Die praktische Konsequenz für Entwickler und Forscher im Bereich des maschinellen Lernens ist daher klar: Wer schnelle Generalisierung und eine robuste Trainingsdynamik anstrebt, sollte Muon als Optimierer in Betracht ziehen.
Dies gilt insbesondere für große, komplexe Netzwerke, die mit umfangreichen und vielschichtigen Datenmengen arbeiten. Eine frühere Freischaltung des Grokking-Effekts bedeutet weniger Trainingszeit, geringeren Ressourcenverbrauch und potenziell bessere Endmodelle. Interessant sind auch die theoretischen Implikationen der Muon-Technologie. Das Zusammenspiel von spektralen Normbeschränkungen und der Newton-Schulz-Iteration führt zu einer impliziten Regularisierung, die Modelle von oberflächlichen Lösungen weg und hin zu tieferen, robusteren Mustern führt. Es scheint, dass gerade dieser zweite Ordnungseffekt, der über die bloße Anpassung der Lernrate hinausgeht, entscheidend für den Erfolg bei der Beschleunigung von Grokking ist.
Solche Innovationen beflügeln die Hoffnung, dass künftig noch leistungsfähigere und intelligentere Modelle entstehen, die selbst komplexe Generalisierungsaufgaben zuverlässig und effizient lösen. Die Entwicklung von Muon reiht sich ein in eine Vielzahl neuer Optimierungsansätze, die gerade das Feld des maschinellen Lernens prägen. Neuere Arbeiten zeigen immer wieder, dass zahlreiche bekannte Optimierer wie Adam, Shampoo oder Prodigy auf fundamentale mathematische Prinzipien wie das steilste Gefälle bezüglich bestimmter Normen zurückgeführt werden können. Die Erforschung dieser Zusammenhänge erweitert das Verständnis von Optimierungsalgorithmen und eröffnet neue Pfade für die effiziente Modellanpassung. Insbesondere Methoden, die Newton-Schulz-Iteration oder andere Matrix-Operationen einbinden, gewinnen zunehmend an Bedeutung.
Muon ist daher nicht nur leistungsfähiger Optimierer, sondern auch Symbol einer neuen Generation von Algorithmen, die auf tiefergehenden mathematischen Einsichten basieren. Ihre Fähigkeit, Modelle nachhaltiger zu steuern und Trainingsergebnisse vorhersehbarer zu machen, wird zum Schlüssel für Fortschritte bei großen Sprachmodellen, komplexen neuronalen Architekturen oder spezialisierten Anwendungsfällen. Zusammenfassend lässt sich sagen, dass der Einsatz des Muon-Optimierers sowohl praktisch als auch theoretisch einen bedeutenden Schritt nach vorne darstellt. Seine Wirkung auf das Grokking-Phänomen macht Trainingsprozesse nicht nur schneller, sondern potenziell auch stabiler und nachhaltiger. Für die Forschung bedeutet dies neue Perspektiven zur Erforschung von Lern- und Generalisierungsmechanismen.
Für die Praxis heißt es verbesserte Effizienz und genauere Modelle – Faktoren, die für die Zukunft des maschinellen Lernens entscheidend sind. Das Zitat von Noam Shazeer aus dem Jahr 2020 erinnert daran, wie viel Magie trotz aller Technik im Bereich künstlicher Intelligenz noch steckt: „Wir bieten keine Erklärung dafür, warum diese Architekturen zu funktionieren scheinen; wir schreiben ihren Erfolg, wie allem, die göttliche Wohltätigkeit zu.“ Mit Muon und ähnlichen Optimierern kommen wir dieser göttlichen Wohltätigkeit Schritt für Schritt etwas näher, indem wir besser verstehen, wie Lernen wirklich funktioniert und wie man es gezielt beschleunigen kann. Die Zukunft wird zeigen, wie sich Muon in größeren, praktisch relevanten Anwendungen bewährt. Erste Ergebnisse sind vielversprechend, und die Community wartet gespannt auf weiterführende Untersuchungen mit unterschiedlichen Modellen und Aufgaben.
Der Trend zu immer spezielleren, mathematisch fundierten Optimierern wird die Landschaft des maschinellen Lernens nachhaltig prägen und robuster, effizienter und kreativer machen.