Die Erforschung topologischer Materialien hat in den letzten Jahren die Festkörperphysik revolutioniert und neue Konzepte in der Quantenphysik greifbar gemacht. Besonders spannende Entwicklungen ergeben sich durch die Kombination von Topologie und elektronischer Korrelation, wodurch neuartige Zustände wie Oberflächen-Supraleitung entstehen können. Die jüngste Entdeckung, dass in dem Dirac-Nodal-Linien-Halbleiter ZrAs2 eine zweidimensionale Supraleitung ausschließlich auf den Oberflächen innerhalb der Kristallebenen ausgebildet wird, markiert einen bedeutenden Fortschritt in der Erforschung solcher Quantenzustände. Dabei spielt eine Van-Hove-Singularität (vHs) eine entscheidende Rolle, die dort nahe der Fermi-Energie lokalisiert ist und die elektronische Dichte der Zustände anhebt, wodurch Supraleitung stabilisiert wird. Topologische Phasen sind in der Festkörperphysik durch spezielle Energie-Impuls-Dispersionen gekennzeichnet, die Dirac- oder Weyl-Knoten zeigen, bei denen sich Bänder im Impulsraum kreuzen und quasiteilchenähnliche Anregungen erzeugen.
Diese können null-, eindimensionale Punkt-Knoten oder auch eindimensionale Linien oder Schleifen sein, wie bei Nodal-Linien-Halbleitern. Solche Materialien besitzen oft charakteristische Oberflächenzustände, sogenannte drumhead states, und können resonanzartige Erhöhungen in ihrem elektronischen Zustandsdichteprofil, die Van-Hove-Singularitäten, aufweisen. Diese Singularitäten resultieren aus Sattelpunkten in der Bandstruktur, an denen sich die Krümmung der elektronischen Bänder verändert, und führen zu einer divergenten Zustandsdichte. Die Verbindung zwischen vHs und Supraleitung ist kein neues Phänomen, wird aber in topologischen Halbleitern mit ihrer komplexen Bandstruktur eine besondere Bedeutung zugeschrieben. Eine Van-Hove-Singularität in zwei Dimensionen kann die elektronische Kopplung und Korrelation drastisch verstärken, was die Bildung von Cooper-Paaren begünstigt.
In ZrAs2 zeigt sich erstmals, dass gerade die Oberflächen im ab-Ebenen-Bereich eine solche Singularität nahe der Fermi-Energie beherbergen und genau hier die Supraleitung entsteht. Anders als bei 3D-Supraleitern ist der beobachtete Übergang zweidimensional, was für Oberflächenzustände typisch ist und sich experimentell am Verhalten der Übergangstemperatur und des kritischen Magnetfeldes manifestiert. Die experimentellen Belege für diese Oberflächen-Supraleitung sind vielfältig. Transportmessungen zeigen bei tiefen Temperaturen einen plötzlichen Abfall des elektrischen Widerstandes auf Null, was typisch für einen Supraleitungsübergang ist. Die Anisotropie des kritischen Magnetfeldes und die charakteristische Winkelabhängigkeit des Übergangs stimmen dabei mit Modellen überein, die eine zweidimensionale Natur der Supraleitung nahelegen.
Zudem lässt sich der Übergang in die Supraleitung durch einen Berezinskii–Kosterlitz–Thouless (BKT)-Übergang beschreiben, der typisch für zweidimensionale Supraleiter ist und durch das Auftreten und die Kopplung von Vortex-Antivortex-Paaren geprägt ist. Solche Effekte sind in dreidimensionalen Materialien nicht beobachtbar und bestätigen somit die Oberflächenlokalisation. Interessanterweise bleibt in den magnetischen Messungen, etwa durch den Meißner-Effekt oder Muonenspinresonanz-Untersuchungen (μSR), die erwartete diamagnetische Signatur aus. Dies wird durch das Fehlen bulk-bezogener Supraleitungsvolumen erklärt, da die Supraleitung auf wenige Schichten an der Oberfläche begrenzt ist und somit für volumenabhängige Methoden praktisch unsichtbar bleibt. Die Oberflächen-Supraleitung ist folglich ein intrinsisches Phänomen der zweidimensionalen Grenzflächen und nicht auf Proximity-Effekte von angrenzenden Schichten zurückzuführen.
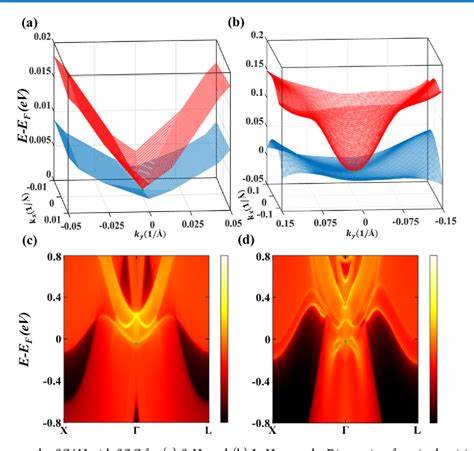
Die theoretischen Berechnungen, insbesondere auf Basis von Dichtefunktionaltheorie (DFT) inklusive Spin-Bahn-Kopplung, bestätigen die Existenz topologischer Nodal-Linien in der Bandstruktur von ZrAs2. Mehrere Nodal-Linien bilden konzentrische Schleifen um bestimmte symmetrische Punkte im Impulsraum, die durch kristallographische Spiegel- und Gleitspiegel-Symmetrien geschützt sind. Die Oberfläche projiziert spezielle Bandzustände mit charakteristischen Sättelpunkten, die als Van-Hove-Singularitäten sichtbar sind. Die Abbildung der Bandstruktur mittels winkelaufgelöster Photoelektronenspektroskopie (ARPES) liefert experimentelle Bestätigung dieser vHs direkt auf der Oberfläche, wobei die Photonenergieabhängigkeit der Messungen die zweidimensionale Natur der Oberflächenzustände belegt. Die enge räumliche Kopplung zwischen zwei-dimensionaler Oberflächen-Supraleitung und der Van-Hove-Singularität bietet eine bisher einmalige Plattform, um die Wechselwirkung zwischen Topologie, elektronischen Korrelationen und quantenmechanischen Phasenübergängen zu untersuchen.
Von besonderem Interesse ist dabei die Möglichkeit, durch gezielte Abänderungen der Oberflächenbandstruktur, zum Beispiel durch chemische Dotierung oder externe Felder, die elektronische Kopplung weiter zu modulieren und zu steuern. Die starke elektronische Korrelation infolge der vHs kann zudem auf unkonventionelle Kopplungsmechanismen hinweisen. Messungen zeigen einen hohen Wert des Verhältnisses zwischen der Supraleitungslücke und der Übergangstemperatur, was auf stark gekoppelte Paare und mögliche exotische Paarungszustände hindeutet. Daraus könnten sich weitere Effekte wie topologische Supraleitung oder Majorana-Zustände ergeben, die für Quantentechnologien von hoher Bedeutung sind. Diese Entdeckungen eröffnen auch praktische Perspektiven.
Das Auftreten robuster Supraleitung auf den Oberflächen topologischer Halbleiter bedeutet, dass zukünftig Quantengeräte entwickelt werden können, die von den besonderen elektronischen Zuständen und der Schutzfunktion der Topologie profitieren. Diese könnten eine hohe Stabilität gegenüber Störungen und Defekten aufweisen und damit Vorteile gegenüber herkömmlichen technisch genutzten Materialien bieten. Vergleichbare Oberflächen-Supraleitungen wurden zuvor vermutet, z.B. in CaAgP oder PtBi2, doch blieb die experimentelle Evidenz und Charakterisierung lückenhaft.