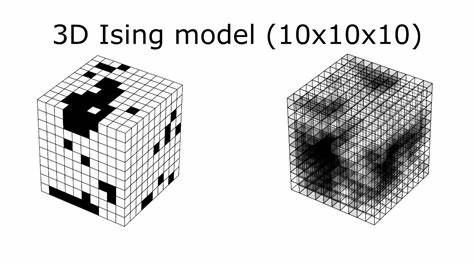
Das 3D Ising Modell nimmt in der Welt der theoretischen Physik eine herausragende Rolle ein. Es handelt sich dabei um ein einfaches, aber kraftvolles Modell, das verwendet wird, um das Verhalten spinbasierter Systeme zu verstehen, insbesondere im Kontext magnetischer Phasenübergänge. Seit seiner Einführung hat es eine Fülle von Forschung inspiriert und ist heute ein unverzichtbares Werkzeug, um fundamentale Konzepte der statistischen Mechanik und der Phasenübergänge zu illustrieren. Mit dem Fortschritt der Computertechnik und der Verfügbarkeit leistungsfähiger Rechenressourcen können solche Modelle nun auch interaktiv und in Echtzeit simuliert werden, was nicht nur Wissenschaftlern, sondern auch Studenten und Physikbegeisterten einen direkten Zugang zu komplexen physikalischen Prinzipien ermöglicht. Im Kern beschreibt das 3D Ising Modell ein Gitter aus Spins, die nur zwei Zustände annehmen können – entweder aufwärts oder abwärts.
Diese Spins interagieren mit ihren Nachbarn und versuchen, eine energetisch günstige Konfiguration zu finden. Das Modell untersucht die Wettbewerbsdynamik zwischen ferromagnetischen und antiferromagnetischen Wechselwirkungen sowie den Einfluss von äußeren Magnetfeldern. Besondere Aufmerksamkeit gilt dabei der kritischen Temperatur, bei der das System einen Phasenübergang durchläuft – vom geordneten ferromagnetischen zu einem ungeordneten paramagnetischen Zustand. Die Simulation eines 3D Ising Modells auf einer Web-basierten Monte-Carlo-Plattform stellt eine innovative Methode dar, um diese theoretischen Konzepte erfahrbar zu machen. Durch den Einsatz von Monte-Carlo-Verfahren lassen sich statistische Eigenschaften eines großen Systems approximativ berechnen, indem zufällige Zustände generiert werden, die den physikalischen Wahrscheinlichkeiten folgen.
So können Nutzer verschiedene Parameter verändern, wie die Temperatur, das äußere Magnetfeld oder die Art der Wechselwirkung, und unmittelbar sehen, wie sich das System verhält. Insbesondere die Möglichkeit, bei Temperaturen um 1000 Kelvin zu simulieren – einem Bereich, der nahe der kritischen Temperatur liegt – eröffnet faszinierende Einsichten. Die kritische Temperatur ist jener Punkt, an dem das System von einem geordneten Zustand in einen ungeordneten übergeht. Bei T=1000 K, entsprechend dem kritischen Temperaturbereich, lässt sich beobachten, wie die Magnetisierung fast an null tendiert und die energetischen Fluktuationen maximal werden. Diese Phänomene sind charakteristisch für kritische Punkte in der Physik und helfen zu verstehen, wie mikroskopische Wechselwirkungen makroskopische Eigenschaften beeinflussen.
Die Visualisierung einer einzelnen Scheibe des Gitters bei z=32 zeigt exemplarisch die räumliche Verteilung der Spins und deren Dynamik unter verschiedenen Bedingungen. Dies macht die komplexen räumlichen Strukturen begreifbar, die in einem dreidimensionalen System entstehen. Die Magnetisierung mit einem Wert von etwa -0,054 zeigt, dass das System nahe an einer ungeordneten Phase ist, während die energiespezifischen Werte pro Gitterpunkt einen Einblick in die energetischen Stabilitäten des Systems geben. Eine weitere spannende Facette ist die Unterscheidung zwischen paramagnetischen, ferromagnetischen und antiferromagnetischen Zuständen. Das interaktive Simulator-Tool erlaubt es, durch die Änderung des Verhältnisses von Para- zu Ferro- und Antiferro-Wechselwirkungen unterschiedliche physikalische Szenarien abzubilden.
Während ferromagnetische Wechselwirkungen dazu neigen, Spins in dieselbe Richtung auszurichten, wirken antiferromagnetische Wechselwirkungen so, dass benachbarte Spins entgegengesetzt ausgerichtet sind. Die Balance dieser Kräfte beeinflusst maßgeblich die Eigenschaften und die Stabilität des Systems. Die Rolle äußerer Magnetfelder im Ising Modell ist ebenfalls einer intensiven Untersuchung wert. Bei null äußeren Feldern entsteht ein natürliches Gleichgewicht der Spins. Durch das Einführen eines Feldes kann das System stabilisiert oder destabilisiert werden, was sich unmittelbar auf die Magnetisierung auswirkt.
Dieses Verhalten demonstriert anschaulich, wie äußere Einflüsse physikalische Systeme steuern können. Die webbasierte Monte-Carlo-Simulation des 3D Ising Modells bietet eine ideale Plattform für wissenschaftliche Bildung und Forschung. Sie ermöglicht es nicht nur, komplexe Berechnungen durchzuführen, sondern unterstützt auch das intuitive Verständnis, indem Veränderungen direkt visuell nachvollzogen werden können. Durch die Online-Verfügbarkeit entfällt zudem die Notwendigkeit leistungsfähiger Rechenhardware vor Ort, was den Zugang zu hochkomplexen Simulationen demokratisiert. In der Forschung spielt das 3D Ising Modell weiterhin eine kritische Rolle bei der Vorhersage von Materialeigenschaften, insbesondere im Bereich der modernen Festkörperphysik und der Magnetismusforschung.
Neue Materialklassen, wie beispielsweise Spintronic-Materialien oder komplexe magnetische Supraleiter, können mit Hilfe solcher Simulationsmodelle analysiert werden. Dies unterstützt die Entwicklung innovativer Technologien und die Erweiterung unseres Verständnisses von magnetischen Phänomenen. Zusätzlich zu den physikalischen Anwendungen ist das 3D Ising Modell auch in anderen Disziplinen von Bedeutung. Es findet Anwendung in der statistischen Theorie komplexer Netzwerke und sogar in der Soziologie, wo es genutzt wird, um das Verhalten von Individuen in Gruppen unter dem Einfluss lokaler Wechselwirkungen zu modellieren. Die Vielseitigkeit dieses Modells macht seine Simulation in interaktiver Form zu einem wertvollen Werkzeug für multidisziplinäre Forschungen.