Mechanische Instabilitäten sind in der Ingenieurwissenschaft oft als unerwünschte Phänomene betrachtet worden. Klassische Beispiele sind das plötzliche Umklappen eines Regenschirms bei Windböen oder das Knicken eines dünnen Stabes unter Druck. Jedoch zeigen natürliche Systeme wie die Venusfliegenfalle oder der Fangmechanismus des Fangschreckenkrebses eindrucksvoll, wie solche Instabilitäten geschickt genutzt werden können. In jüngster Zeit ist die Forschung darauf ausgerichtet, diese nichtlinearen Effekte auch in künstlichen Materialien und Strukturen einzusetzen, um außergewöhnliche und programmierbare mechanische Eigenschaften zu schaffen. Ein faszinierender Fortschritt ist die experimentelle Realisierung sogenannter Countersnapping-Instabilitäten, welche konventionelle Erwartungen an die Richtung und Reaktion mechanischer Systeme fundamental herausfordern.
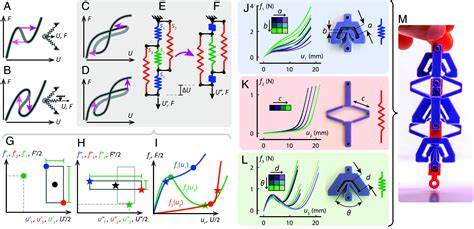
Im Gegensatz zu gewöhnlichen Schnappvorgängen, bei denen die Verformung in Richtung der aufgebrachten Kraft erfolgt, zeichnet sich Countersnapping durch eine konträre Reaktion aus. Konkret bedeutet dies, dass unter zunehmender Zugspannung eine plötzliche Verringerung der Länge stattfindet oder bei zunehmender Verlängerung die aufgenommene Zugkraft plötzlich ansteigt. Eine solche Gegenreaktion ist überraschend, da sie einem intuitiven Verständnis mechanischer Verformungen widerspricht und bislang weder in natürlichen Systemen beobachtet noch im technischen Bereich praktisch umgesetzt worden war. Der Schlüssel zu dieser Entdeckung liegt in der Kombination und Kopplung von Bauelementen mit unterschiedlichen nichtlinearen geometrischen Eigenschaften. Durch die exakte Abstimmung von weichen, versteifenden und nichtmonotonen mechanischen Feder-ähnlichen Komponenten kann eine Struktur entstehen, deren Kraft-Weg-Kurven selbstüberschneidende Zustände besitzen.
Diese Selbstüberschneidung führt dazu, dass eine vermeintlich kleine Erhöhung der Zugkraft eine abrupte Kontraktion und eine signifikante Erhöhung der Zugspannung bewirkt – der Countersnap-Effekt. Die praktische Umsetzung erfolgt durch den modularen Aufbau kleiner Netzwerke aus drei definierten Bauelementtypen: einem softening (weicher werdenden) Element, einem stiffening (steifer werdenden) Element und einem nonmonotonic (nichtmonotonen) Element. Diese Bauelemente können durch einfache geometrische Formen wie V-förmige Paarungen von geneigten Balken oder diamantförmige Anordnungen realisiert werden, die durch Druck- und Zugbelastungen unterschiedliche Verformungsmuster zeigen. Durch den Zusammenbau entstehen komplexe Energiepotenziale, die die ungewöhnlichen Countersnapping-Phänomene ermöglichen. Experimentell konnte das Countersnapping an maßstabsgetreuen Prototypen aus elastischen Materialien wie Silikongummi nachgewiesen werden.
Bei kontrollierter Verlängerung zeigte sich in der Kraft-Weg-Kurve ein sprunghafter Anstieg der Zugkraft, während eine weitere Kontrolle der Zugkraft zu einer abrupte Kontraktion führte – ein eindeutiges Messergebnis für die Existenz des Countersnapping-Effekts. Selbst Simulationen mit umfangreichen Variationen der Parameter bestätigten die Existenz dieses Phänomens, wobei hervorgehoben wurde, dass die Fenster zur praktischen Realisierbarkeit relativ eng sind und präzises Design erfordern. Die mechanischen Konsequenzen dieses Effekts sind vielfältig und eröffnen neue Anwendungsmöglichkeiten. Einer der interessantesten Aspekte ist die Fähigkeit zu einem unidirektionalen Stick-Slip-Phänomen. Während herkömmliche Schnappstrukturen unter zyklischer Belastung wiederholt vor- und zurückschnappen und somit kaum eine Nettobewegung erzeugen, bewirkt Countersnapping bei jedem Zyklus eine Bewegung in dieselbe Richtung.
Das ermöglicht eine schrittweise Vorwärtsbewegung ohne komplexes Antriebs- oder Steuerungssystem und könnte in Bereichen wie präziser Mikropositionierung, Sensoren zur Zykluserkennung oder weichen Robotern mit lokaler Bewegungssteuerung eingesetzt werden. Ein weiteres faszinierendes Ergebnis ist die sogenannte programmierbare Steifigkeit bei unverändertem Gleichgewichtszustand. Am Schnittpunkt der Kraft-Weg-Kurve existieren zwei unterschiedliche Zustände mit identischem Kraft- und Längenwert, jedoch unterschiedlicher Steifigkeit. Durch gezieltes Auslösen des Countersnapping kann somit der Elastizitätsmodul eines Bauteils geschaltet werden, ohne dass sich die äußeren Randbedingungen ändern. Dies eröffnet neue Perspektiven für adaptive mechanische Systeme, welche zum Beispiel ihre Resonanzeigenschaften dynamisch an Umgebungsveränderungen anpassen können.
Die passive Selbstumschaltung der Steifigkeit bei Anregung nahe der Resonanzfrequenz zeigt vielversprechende Ansätze für vibrierende Systeme, die sich autonom von schädlichen Schwingungen schützen. Noch komplexer wird das Verhalten, wenn mehrere Countersnapping-Elemente miteinander gekoppelt werden. Parallel geschaltete Einheiten erlauben eine abgestufte Änderung der Gesamtsteifigkeit, während sich die äußeren Größen praktisch nicht ändern. Dadurch sind fein abgestufte mechanische Programme realisierbar. In serieller Anordnung können Countersnapping-Elemente kollektive, sogenannte Avalanche-Übergänge auslösen, wo alle Elemente nahezu gleichzeitig von einem Zustand in den anderen wechseln.
Dies steht in starkem Gegensatz zu klassischen Schnappstrukturen, bei denen eine Verformung oft eine Stabilisierung der Nachbarelemente erzeugt. Im Gesamtkontext stellen Countersnapping-Instabilitäten eine neue Klasse von nichtlinearen mechanischen Systemen dar, die bisherige Grenzen in der Steuerung und Programmierung mechanischer Eigenschaften sprengen. Die experimentelle Realisierung auf Basis einfach herstellbarer elastischer Bauteile zeigt, dass solche Konzepte nicht nur theoretische Kuriositäten sind, sondern praktische Anwendungen in der Zukunft finden können. Herausforderungen bleiben allerdings bestehen. Die aktuell verwendeten Muster sind vergleichsweise groß und empfindlich gegenüber Fertigungstoleranzen.
Die Miniaturisierung und die Integration in komplexere Systeme erfordern optimierte Konstruktionen und Materialien. Darüber hinaus bieten Countersnapping-Phänomene Potenzial in verwandten Bereichen wie Fluidik, Elektronik oder sogar biomedizinischen Anwendungen, indem ähnliche Selbstüberschneidungen in anderen physikalischen Variablen genutzt werden. Die Erforschung aktiver Materialien wie thermo-responsive, lichtempfindliche oder magnetisch aktive Komponenten könnte zudem neue Wege eröffnen, Countersnapping gezielt und reproduzierbar zu steuern, womit flexiblere und rekonfigurierbare Systeme realisierbar wären. Damit rücken adaptive Materialien und smarte Strukturen, die sich dynamisch an ihre Umwelt anpassen, in greifbare Nähe. Insgesamt markieren Countersnapping-Instabilitäten einen wichtigen Meilenstein auf dem Weg zu mechanischer Intelligenz, die weit über klassisches Design hinausgeht.