Lyapunov-Zeit: Schlüssel zur Vorhersagbarkeit chaotischer Systeme verstehen

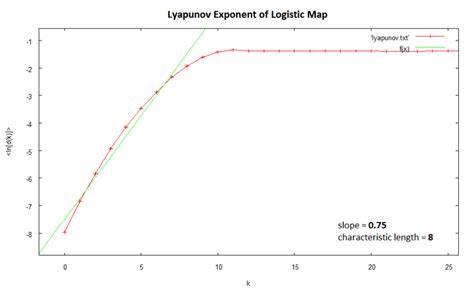
Die Lyapunov-Zeit ist eine fundamentale Größe in der Theorie dynamischer Systeme, die uns Aufschluss darüber gibt, wie lange ein System verlässlich prognostiziert werden kann, bevor die Vorhersage aufgrund seiner chaotischen Natur zunehmend ungenau wird. Benannt nach dem russischen Mathematiker Aleksandr Lyapunov, beschreibt sie den charakteristischen Zeitraum, in dem kleine Unterschiede in Anfangsbedingungen exponentiell anwachsen und somit die Entwicklung des Systems grundlegend verändern können. Dieses Konzept hat weitreichende Anwendungsgebiete, von der Himmelsmechanik über chemische Reaktionen bis hin zu physikalischen Prozessen auf molekularer Ebene. Das Kernprinzip hinter der Lyapunov-Zeit beruht auf der Messung der größten Lyapunov-Exponenten eines Systems. Diese Exponenten quantifizieren die durchschnittliche Wachstumsrate von Abständen zwischen zwei ursprünglich nahe beieinanderliegenden Systemzuständen über die Zeit.

Die Lyapunov-Zeit wird als der Kehrwert dieses größten Exponenten definiert, was intuitiv betrachtet die Zeit darstellt, in der sich nahe beieinanderliegende Trajektorien um den Faktor e (die Eulersche Zahl, ungefähr 2,718) voneinander entfernen. Dieses Wachstum des Abstands weist auf ein exponentielles Auseinanderdriften von Bahnen hin, das typisch für chaotisches Verhalten ist. Die Bedeutung der Lyapunov-Zeit liegt vor allem in ihrem Bezug zur Vorhersagbarkeit eines Systems. Innerhalb dieser Zeitspanne sind Modelle und Simulationen recht zuverlässig, wobei kleinste Unsicherheiten in den Anfangsbedingungen nur begrenzten Einfluss auf die Gesamtprognose haben. Nach Ablauf der Lyapunov-Zeit jedoch wächst die Unsicherheit so stark an, dass Vorhersagen praktisch unmöglich werden – die Systementwicklung wird dadurch unvorhersehbar.

In der Himmelsmechanik ist die Lyapunov-Zeit von herausragender Bedeutung, da sie Einblick in die Stabilität und Entwicklung von Planetensystemen bietet. Die Bewegung der Himmelskörper unterliegt zahlreichen komplexen Wechselwirkungen, die als nicht-linear und potenziell chaotisch gelten. Studien haben gezeigt, dass orbitalen Bewegungen innerhalb unseres Sonnensystems Lyapunov-Zeiten im Bereich von mehreren Millionen Jahren aufweisen. Zum Beispiel wird die Umlaufbahn von Pluto auf eine Lyapunov-Zeit von etwa 20 Millionen Jahren geschätzt, während das gesamte Sonnensystem eine ungefähre Zeitskala von rund fünf Millionen Jahren besitzt. Diese Zeiträume verdeutlichen, dass die langfristigen Prognosen astronomischer Bahnen aufgrund des chaotischen Verhaltens immer mit Unsicherheiten behaftet bleiben.

Eine weitere eindrucksvolle Anwendung findet sich in der Untersuchung von Mars' Achsneigung. Die Achsneigung beeinflusst maßgeblich das Klima und die Jahreszeiten eines Planeten. Für Mars beträgt die Lyapunov-Zeit der Neigung zwischen ein bis fünf Millionen Jahren, was bedeutet, dass langfristige Klimamodelle erhebliche Unsicherheiten enthalten können. Dies wirkt sich direkt auf die Planung zukünftiger Missionen und das Verständnis der planetaren Entwicklung aus. Aber die Bedeutung der Lyapunov-Zeit beschränkt sich nicht nur auf astronomische Skalen.

Auch in kleineren Maßstäben und anderen wissenschaftlichen Disziplinen eröffnet sie neue Einsichten. So findet sich beispielsweise der chaotische Tanz des Saturnmonds Hyperion, dessen Rotation eine Lyapunov-Zeit von etwa 36 Tagen aufweist. Dieses ungewöhnliche Phänomen ist ein Beispiel für einen rotierenden Körper, dessen Bewegung sich nur über kurze Zeiträume genau vorhersagen lässt. Im Bereich der experimentellen Chemie sind chaotische Oszillationen bekannt, beispielsweise im Belousov-Zhabotinsky-Reaktionssystem. Dort erfolgt eine zyklische Änderung der Konzentrationen chemischer Substanzen, wobei die Lyapunov-Zeit im Bereich von Minuten bis wenigen Sekunden liegt.

Solche chaotischen Reaktionen bieten wertvolle Modelle, um nichtlineare Dynamik zu verstehen und für technische Anwendungen wie Prozesssteuerungen oder neue Materialentwicklungen zu nutzen. Selbst auf mikroskopischer Ebene gibt die Lyapunov-Zeit Auskunft über das Verhalten von Molekülen in Gasmischungen. Für 1 cm3 Argongas bei Raumtemperatur liegt die Lyapunov-Zeit bei winzigen Werten von rund 3,7×10^−11 Sekunden, während sie bei niedrigeren Temperaturen und Druckverhältnissen, wie am Triplepunkt, noch deutlich kürzer wird. Diese extrem kurzen Zeiten zeigen die schnelle Divergenz dynamischer Bahnen in molekularen Systemen und stellen eine Herausforderung für numerische Simulationen dar. Die präzise Berechnung und Abschätzung der Lyapunov-Zeit ist jedoch nicht trivial.

Sie erfordert umfangreiche numerische Verfahren und wird durch die Komplexität der zugrunde liegenden Modelle erschwert. In der Praxis sind Schätzungen häufig mit Unsicherheiten verbunden, zum Teil bedingt durch Rechenleistung und numerische Genauigkeit, zum Teil aber auch wegen inhärenter systembedingter Schwankungen. Dies spiegelt wider, dass Chaostheorie keine deterministischen, sondern probabilistische Aussagen über das Verhalten komplexer Systeme liefert. Neben der reinen wissenschaftlichen Relevanz hat das Konzept der Lyapunov-Zeit auch philosophische und praktische Auswirkungen auf unser Verständnis von Determinismus und Zufall in der Natur. Es verdeutlicht, dass selbst bei angeblich bekannten Anfangsbedingungen langfristige Vorhersagen oft nur begrenzt möglich sind und die Welt in ihrer Dynamik häufiger unvorhersehbar bleibt, als intuitiv vermutet wird.

In den letzten Jahren wurden interessante Verbindungen zwischen der Lyapunov-Zeit und anderen Konzepten der Informations- und Theorie der Dynamik gefunden. So lässt sich die maximale Lyapunov-Exponenten mathematisch mit Kanalkapazitäten aus der Informationstheorie in Beziehung setzen, was zeigt, wie chaotische Systeme als Informationskanäle betrachtet werden können, deren Übertragungsgenauigkeit durch die Lyapunov-Zeit begrenzt ist. Zusammenfassend lässt sich sagen, dass die Lyapunov-Zeit ein mächtiges Werkzeug ist, um die Grenzen der Vorhersage in einer Vielzahl von dynamischen Systemen zu bestimmen. Von der Stabilität planetarer Bahnen über chemische Oszillationen bis hin zu molekularen Bewegungen ist sie der Schlüssel zum Verständnis chaotischer Prozesse. Ihre Bedeutung reicht über die Mathematik hinaus und bietet zentrale Einsichten in viele wissenschaftliche Disziplinen und Anwendungen.

Durch die Betrachtung der Lyapunov-Zeit gewinnen wir nicht nur ein tieferes Verständnis der komplexen Natur der Systeme um uns herum, sondern auch eine realistische Einschätzung ihrer Prognosefähigkeit und der Herausforderungen, die sich daraus für Forschung und Technologie ergeben.