Die Fibonacci-Folge und die goldene Ratio Phi haben seit Jahrhunderten die Fantasie von Wissenschaftlern, Künstlern und Mystikern gleichermaßen beflügelt. Insbesondere im Internet und populären Medien werden oft erstaunliche Behauptungen aufgestellt, die der Mathematik und Naturwissenschaft nur wenig gerecht werden. Doch was steckt wirklich hinter den Zahlen, die auf den ersten Blick nahezu magisch erscheinen? Wie viel Wahrheit steckt in der Idee, dass die Fibonacci-Folge und die goldene Ratio das Geheimnis der Schönheit und Ordnung in der Natur bilden? Ein nüchterner, kritischer Blick bringt notwendige Klarheit. Leonardo von Pisa, besser bekannt als Fibonacci, lebte Anfang des 13. Jahrhunderts und ist vor allem durch eine Zahlenfolge berühmt geworden, die nach ihm benannt ist.
Die Fibonacci-Folge beginnt meist mit den Zahlen 0 und 1 (manchmal auch mit 1 und 1) und setzt sich fort, indem jede neue Zahl die Summe der beiden vorhergehenden ist. So entsteht eine Reihe von Zahlen wie 0, 1, 1, 2, 3, 5, 8, 13, 21 und so weiter. Diese einfache rekursive Regel erzeugt eine Reihe von Zahlen, die weitreichende und teils unerwartete mathematische Eigenschaften aufweist. Eine der wohl bekanntesten Eigenschaften ist, dass sich der Quotient zweier aufeinanderfolgender Fibonacci-Zahlen mit zunehmender Folge der Zahl Phi nähert, auch bekannt als goldene Zahl oder goldener Schnitt, etwa 1,61803. Dieses Verhältnis wurde schon in der Antike beschrieben und war den Griechen wohlbekannt.
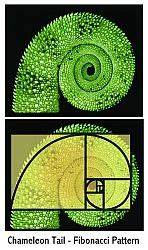
Es ist in der Geometrie ein spezielles Verhältnis, das ästhetisch anmutende Proportionen erzeugen kann – zumindest theoretisch. Doch gerade diese Assoziationen haben viele zu einer Art Mythenbildung und übertriebener Verehrung der Fibonacci-Zahlen und der goldenen Ratio geführt. Im Bereich der Natur etwa ist oft zu hören, dass sich Blätterbeformungen an Pflanzen, Spiralen von Sonnenblumenkernen oder Schneckenhäusern exakt an der Fibonacci-Folge oder an goldenes Verhältnis orientieren würden. Solche Behauptungen halten bei näherem Hinsehen jedoch selten einer rigorosen Prüfung stand. Pflanzenwachstum und natürliche Formen sind das Ergebnis komplexer biologischer Prozesse, physikalischer Zwänge und Zufälle.
Wenn sich Muster zeigen, sind diese eher durch geometrische und mechanische Ursachen bedingt statt durch eine zugrundeliegende "mathematische Ordnung" göttlicher Art. Ein prominentes Beispiel des Missverständnisses ist die Behauptung, das Gehäuse der Schalennautilus folge perfekt der Form einer goldenen Spirale, einem logarithmischen Spiraltyp, der auf der Fibonacci-Folge basiert. Tatsächlich weichen reale Schneckenhäuser oft deutlich von der idealisierten Form ab. Die tatsächliche Krümmung und der Verlauf der Spirale variieren und sind nicht exakt mit der mathematischen Goldenen Spirale vereinbar. Ebenso ist das Auftreten von Fibonacci-Zahlen in der Zahl der Blütenblätter oder der Spiralrichtungen von Tannenzapfen zwar oft zu beobachten, aber längst nicht universell und kein Gesetz der Natur.
Ein weiterer verbreiteter mythologischer Teilbereich ist die Verwendung der goldenen Ratio in Kunst, Architektur und Ästhetik. Historische Bauten wie der Parthenon wurden gerne als Beispiel für bewusste Anwendung der goldenen Ratio zitiert. Doch bei genauerer Untersuchung der Baupläne und Maße des Parthenon finden sich kaum Belege für einen gezielten Einsatz dieses Proportionsverhältnisses. Oft handelt es sich hierbei um willkürliche Zuschreibungen oder das selektive Herausgreifen von Abschnitten der Bauwerke, die zufällig näherungsweise zum goldenen Verhältnis passen. Moderne psychologische Studien zur Wahrnehmung von Proportionen zeigen zudem, dass menschliche Präferenzen sehr unterschiedlich sind und vielfach von weitaus banaleren Verhältnissen, etwa 3:4, bestimmt werden.
Das goldene Verhältnis ist also keineswegs der universelle Schlüssel zum ästhetischen Empfinden. Auch in der Musik wird manchmal ein Zusammenhang mit der goldenen Zahl behauptet. Manche populäre Erzählungen besagen, Mozart oder andere Komponisten hätten gezielt mit Fibonacci-Relationen gearbeitet. Es gibt jedoch kaum handfeste Beweise für solche Absichten. Vielmehr sind derlei Behauptungen oft reine Spekulationen oder retrospektive Zuschreibungen.
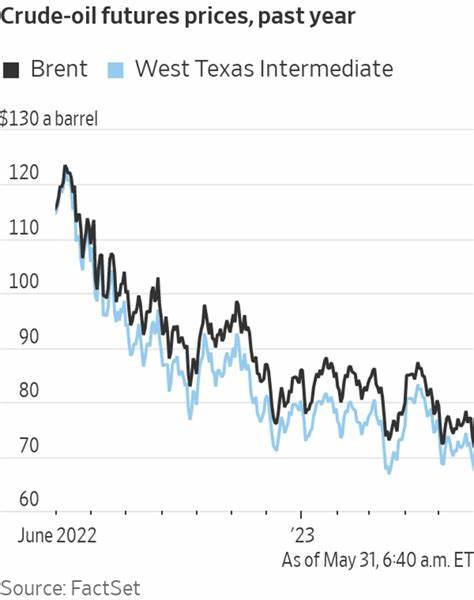
Im Finanzbereich existieren zahllose Trading-Modelle, die Fibonacci-Zahlen und -Verhältnisse als Vorhersageinstrument nutzen wollen. Die Realität zeigt jedoch, dass diese Methoden keine zuverlässigen Vorteile bieten. Finanzmärkte sind komplexe Systeme mit vielen Einflussgrößen und Zufallsfaktoren. Die Mathematik der Fibonacci-Zahlen liefert in diesem Zusammenhang keine magische Formel, sondern häufig eher ein Label, das Anleger falsche Sicherheit suggeriert. Auf den ersten Blick verblüfft die Tatsache, dass einfache rekursive Zahlenfolgen wie die Fibonacci-Folge oder verwandte Lucas-Sequenzen zu irrationalen Grenzwerten führen, die in der Geometrie eine gewisse „Harmonie“ zu erzeugen scheinen.
Diese Zahlen erscheinen in verschiedenen mathematischen Zusammenhängen und können das Wachstum gewisser idealisierter Modelle von natürlichen Formen beschreiben. Trotzdem darf man nicht mit einer übertriebenen Allgegenwärtigkeit und vielschichtigen Bedeutung der Fibonacci-Folge in der realen Welt verwechseln. Das zeigt sich auch bei der sogenannten Phyllotaxis, dem Muster der Blatt- und Sprossanordnung an Pflanzen. Untersuchungen fanden heraus, dass die Winkelabstände zwischen aufeinanderfolgenden Blättern oftmals nahe dem sogenannten goldenen Winkel von etwa 137,5 Grad liegen, der sich aus der goldenen Ratio ableitet. Diese Anordnung ermöglicht eine effiziente Raumnutzung und Belichtung der Blätter.
Dennoch sind die Degressanzahlen und Muster keineswegs immer Fibonacci-Zahlen, es gibt vielfältige Abweichungen und biologische Einflüsse. Das Muster entsteht durch dynamische Wachstumsprozesse, Stofftransport und Zellteilung, nicht durch ein „bewusstes Streben“ der Natur nach bestimmten Zahlen. Die Tendenz, Muster dort zu erkennen, wo Zufälle oder komplexe Prozesse am Werk sind, nennt man apophenia. Es ist ein menschliches Bedürfnis, Ordnung und Sinnhaftigkeit in der Welt zu sehen. Die Fibonacci-Zahlen, die in einigen Fällen tatsächlich auftreten, bieten hierfür eine scheinbar passende Vorlage – leider oft ohne hinreichende wissenschaftliche Fundierung.
Eine weitere Kritik bezieht sich auf den Umgang mit Daten und Messungen. Behauptungen wie die über die Nabelhöhe als proportionellen Anteil an der Körpergröße, der exakt dem Kehrwert der goldenen Ratio entspricht, halten einer Messung an echten Menschen nicht stand. Studien an Models zeigen durchschnittliche Verhältnisse, die von der goldenen Zahl deutlich abweichen. Solche Mythen basieren häufig auf selektiver Wahrnehmung und Wunschdenken. Manche Vertreter pseudowissenschaftlicher oder gar religiös motivierter Ansätze missbrauchen die Fibonacci-Zahlen als Beleg für göttliche Ordnung oder Design in der Natur.
Dabei argumentieren sie oft mit selektiver Beweisführung, Ignorieren von Gegenbeispielen und irrationalen Erklärungen. Dieses Vorgehen ist aus wissenschaftlicher Sicht klar abzulehnen, es gehört in den Bereich der Pseudowissenschaft. Die mathematischen Eigenschaften der Fibonacci-Folge sind zweifellos faszinierend. Sie sind bei weitem nicht einzigartig; viele andere rekursive Sequenzen zeigen ähnliche Konvergenzverhalten, ähnlich wie die Lucas-Folgen. Auch sie zeigen eine große Vielfalt an Verhältnissen und haben interessante, teils verblüffende Eigenschaften.
Die folkloristische Fixierung auf die Fibonacci-Folge verzerrt daher das Bild von der Mathematik und ihrer Beziehung zur Welt. Letztlich sind Fibonacci-Folge, goldener Schnitt und einige verwandte Konzepte Werkzeuge für das Verständnis von Mustern und Wachstumsvorgängen sowie Ästhetiktheorien, deren Anwendung und Interpretation mit Bedacht erfolgen sollten. Sie bieten Raum für spielerische und wissenschaftliche Erkundungen, aber keine mystischen Erklärungen. Die Faszination der Fibonacci-Folge, verstärkt durch schöne Bilder von spiralförmigen Sonnenblumenkernen oder der scheinbaren Magie des goldenen Schnitts, hat ohne Zweifel ihren Platz in der Popularisierung von Mathematik. Doch wer sich tiefergehend mit den Zahlen und ihren Bedeutungen beschäftigt, erkennt die Grenzen und Relativierungen des Trubels um diese Zahlenfolgen.
Wer als Leser also in die Welt der Fibonacci-Zahlen eintaucht, sollte dies mit offenem, aber kritischem Geist tun. Zahlen und Muster bieten spannende Einsichten, aber auch Fallstricke. Rationales Nachdenken und wissenschaftliche Methodik sind unerlässlich, wenn es darum geht, Fakten von Fiktionen zu unterscheiden. So bleibt der Blick auf Fibonacci ein lehrreiches Beispiel dafür, wie Mathematik und Naturwissenschaft Aufklärung leisten und gegen Mythenbildung angehen können.