Chebfun: Präzise numerische Funktionsberechnung mit Open-Source-Power in MATLAB

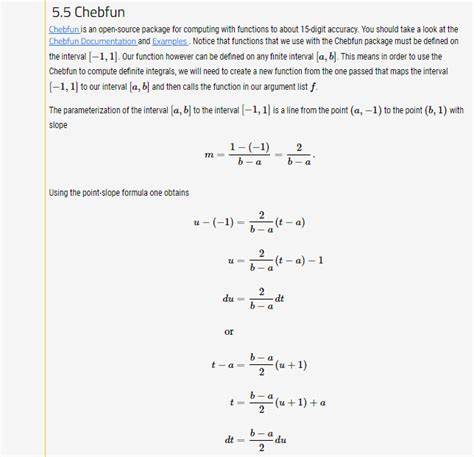
In der modernen numerischen Mathematik ist die genaue Berechnung von Funktionen und deren Eigenschaften von großer Bedeutung. Hier setzt Chebfun an – ein Open-Source-Paket für MATLAB, mit dem Nutzer Funktionen mit nahezu doppelter Maschinenpräzision, also bis zu 15 Stellen Genauigkeit, berechnen können. Chebfun revolutioniert dadurch die Art und Weise, wie numerische Berechnungen mit Funktionen durchgeführt werden, und bietet eine intuitive Alternative zu klassischen diskreten Ansätzen. Chebfun ist im Wesentlichen eine Softwarebibliothek, die das Prinzip der numerischen Approximation von Funktionen mittels Chebyshev-Polynomen nutzt. Dabei wird eine kontinuierliche Funktion durch eine Finite Anzahl von Koeffizienten beziehungsweise Stützpunkten effizient beschrieben, was sowohl Rechenzeit als auch Speicherbedarf optimiert.

Im Gegensatz zu traditionellen Methoden arbeitet Chebfun nicht nur mit diskreten Datenpunkten, sondern behandelt Funktionen als eigenständige mathematische Objekte – ähnlich wie Vektoren oder Matrizen in der linearen Algebra. Die Integration von Chebfun in MATLAB erfolgt so, dass viele vertraute MATLAB-Befehle überladen werden, um mit Funktionen zu arbeiten. So kann beispielsweise der Befehl sum(f) dazu verwendet werden, das Integral einer Funktion f zu berechnen. Ebenso findet roots(f) die Nullstellen der Funktion, und lineare Differentialgleichungen können bequem mit dem Operator L\f gelöst werden, wobei L eine entsprechende Differentialoperatorfunktion ist. Diese intuitive Syntax macht Chebfun besonders für Anwender attraktiv, die bereits MATLAB-Kenntnisse besitzen.

Ein wichtiger Vorteil von Chebfun ist seine Fähigkeit, automatische Anpassungen an die Komplexität der Funktion vorzunehmen. Die Software passt die Anzahl der Stützpunkte während der Approximation dynamisch an, um die höchstmögliche Genauigkeit zu gewährleisten, ohne dabei unnötige Rechenlast zu erzeugen. Das Ergebnis sind exakte numerische Lösungen, die mit herkömmlichen Methoden oft nur schwer machbar sind oder viel mehr Aufwand verursachen würden. Chebfun bietet nicht nur eindimensionale Funktionsapproximationen (chebfun), sondern kann auch mit Zweidimensionalen Funktionen (chebfun2) und sogar dreidimensionalen Funktionen (chebfun3) umgehen. Dies erweitert das Anwendungsspektrum erheblich und erlaubt komplexe Aufgabenstellungen wie das Auffinden von Globalminima auf ebenen Flächen oder die Lösung partielle Differentialgleichungen (PDEs) in mehreren Dimensionen.

Ein bemerkenswertes Beispiel für Chebfuns Leistungsfähigkeit ist die Behandlung der Dixon-Szego-Funktion, eine komplexe zweidimensionale Funktion, die in der Mathematik und Physik als Testobjekt dient. Mit wenigen Zeilen Code kann Chebfun2 auf den definierten Bereich angepasst, das Minimum der Funktion gefunden sowie graphisch dargestellt werden. Durch die nahtlose Verknüpfung von mathematischer Analyse und Visualisierung bietet Chebfun hier enorme Zeitersparnis. Besonders aufsehenerregend ist Chebfuns Modul für die Lösung von Differentialgleichungen, wie beispielsweise das Ginzburg-Landau-Problem. Dieses komplexe nichtlineare Partielle Differentialgleichungssystem kann mit Chebfun in Kombination mit geeigneten Operatoren und Anfangsbedingungen gelöst und der Zeitverlauf visualisiert werden.

Solche Möglichkeiten machen Chebfun in Forschungsgebieten wie Physik, Ingenieurwesen und angewandter Mathematik besonders wertvoll. Auch im Bereich der Quantenmechanik zeigt Chebfun seine Vielseitigkeit. Die Berechnung von Eigenzuständen eines Schrodinger-Operators mit beliebigen Potentialen ist dank der modularen Struktur und der hohen Präzision einfach umsetzbar. Anwender können so effizient die physikalischen Eigenschaften von Quantensystemen simulieren und analysieren, ohne sich mit umständlichen numerischen Details auseinandersetzen zu müssen. Die Benutzerfreundlichkeit von Chebfun zeichnet sich außerdem durch den minimalistischen Installationsprozess aus.

Es läuft direkt in einer Standard-MATLAB-Installation, ohne dass zusätzliche Toolboxes erforderlich sind. Dies ermöglicht einen schnellen Einstieg auch für Anwender, die nicht auf umfangreiche Softwarepakete zugreifen können oder wollen. Umfangreiche Dokumentationen, eine große Anzahl von Beispielcodes sowie eine aktive Anwender-Community tragen dazu bei, den Lernprozess zu vereinfachen. Chebfun bietet zudem leistungsfähige Werkzeuge für die Analyse von Funktionen, wie etwa die Darstellung von Chebyshev-Koeffizienten, Phasenportraits komplexwertiger Funktionen oder das Auffinden gemeinsamer Nullstellen mehrerer Funktionen mittels Resultantenmethoden. Diese Funktionen ermöglichen eine tiefere Einsicht in das Verhalten mathematischer Modelle und unterstützen die explorative Datenanalyse.

Die Projektgeschichte von Chebfun ist ebenso interessant wie die Technik dahinter. Gegründet vor über 20 Jahren an der University of Oxford, hat sich das Paket kontinuierlich weiterentwickelt und ist heute aus der angewandten Mathematik nicht mehr wegzudenken. Die Entwickler haben es sich zum Ziel gesetzt, das Arbeiten mit Funktionen so einfach und mächtig wie das Arbeiten mit Vektoren und Matrizen zu gestalten, was ihnen im großen Maßstab eindrucksvoll gelungen ist. Ein weiterer Aspekt, der Chebfun attraktiv macht, ist seine hervorragende Performance. Trotz der hohen Genauigkeit bleibt die Rechenzeit in akzeptablen Grenzen.

Komplexe Berechnungen, die bei naiven Methoden Stunden oder Tage dauern könnten, sind mit Chebfun oft in wenigen Sekunden oder Minuten erledigt. Das macht es zu einem idealen Werkzeug für Forscher und Ingenieure, die schnelle und zuverlässige Ergebnisse benötigen. Abschließend lässt sich sagen, dass Chebfun mehr als nur ein mathematisches Werkzeug ist – es ist eine neue Philosophie des Rechnens mit Funktionen. Die Kombination aus Open-Source-Zugänglichkeit, weiterführender mathematischer Technik und einfacher Bedienbarkeit eröffnet Anwendern vielfältige Möglichkeiten, Probleme präzise und effizient zu lösen. Ob bei der Ausbildung, Forschung oder in industriellen Anwendungen, Chebfun bietet einen erheblichen Mehrwert für alle, die mit Funktionen und Differentialgleichungen arbeiten.

Die Zukunft von Chebfun verspricht weitere Erweiterungen und Verbesserungen, um noch größere und komplexere Aufgabenstellungen abzudecken. Dank der lebendigen Community und der starken wissenschaftlichen Basis bleibt Chebfun ein unverzichtbarer Begleiter für jeden MATLAB-Anwender, der höchste Genauigkeit bei der Funktionsrechnung verlangt.