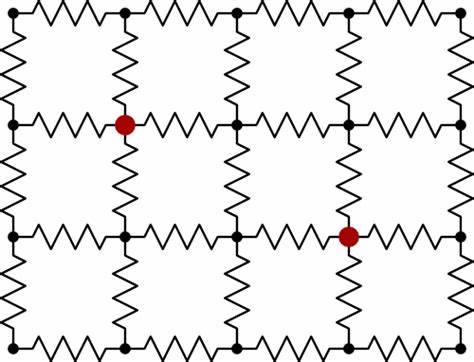
Das unendliche Widerstandsnetz ist ein faszinierendes Konzept, das auf den ersten Blick einfach erscheint, in der Tiefe jedoch eine komplexe und reichhaltige Problematik birgt. Es besteht aus einem Gitter unzähliger Widerstände, die in einem quadratischen Raster miteinander verbunden sind und sich unendlich in alle Richtungen erstrecken. Zwischen benachbarten Knoten befindet sich jeweils ein Widerstand mit einem identischen Wert R. Die grundlegende Fragestellung lautet: Wie berechnet man den effektiven Widerstand zwischen zwei Knotenpunkten eines solchen unendlichen Netzes? Diese scheinbar einfache Frage hat weitreichende Konsequenzen in der Elektrotechnik, der Physik und der mathematischen Theorie von Netzwerken und Laplace-Gleichungen. Bei einem endlichen Widerstandsnetz könnte man die Berechnung mithilfe der klassischen Kirchhoff'schen Gesetze oder der Spannungsteilermethode durchführen.
Die Unendlichkeit des Gitters aber stellt diese Ansätze vor große Herausforderungen, denn die übliche Methode endet hier zwangsläufig in einer unüberschaubaren Anzahl von Gleichungen. Dennoch existieren elegante mathematische und physikalische Methoden, um eine Lösung für bestimmte Fälle zu finden, insbesondere für den Fall zweier benachbarter Knoten. Ein grundlegender Zugang zur Lösung basiert auf dem Prinzip der Superposition und Symmetrie. Wenn man sich vorstellt, an einem Knotenpunkt einen Strom einzuspeisen und an einem benachbarten Knoten den gleichen Strom wieder zu entnehmen, so ergeben sich zwei Spannungsfelder, die sich linear überlagern. Die Spannung an einem Knoten entspricht dabei dem Durchschnitt der Spannungen seiner vier benachbarten Knoten – eine diskrete Version der Laplace-Gleichung.
Dieses Gleichungssystem spiegelt die Tatsache wider, dass Strom in einem solchen Netzwerk sich analog zu elektrischen Potentialen in einem kontinuierlichen Medium verteilt. Unter der Annahme endlicher Widerstände R zwischen den Knoten kann die Symmetrie des Problems dazu genutzt werden, die Verteilung der Stromflüsse zu analysieren. Konkret zeigt sich, dass der Widerstand zwischen zwei benachbarten Knoten im unendlichen Gitter gleich R durch 2 ist. Dieser überraschende Wert wird auch dadurch plausibel, dass der direkte Zweig zwischen den beiden Knoten parallel zu einem unendlichen komplexen Netzwerk wirkt, dessen Widerstand den gleichen Wert annimmt. Trotz dieser anschaulichen Argumentation ist die Situation theoretisch komplexer, da bei einem unendlichen Gitter kein physikalisch realistischer Zustand wirklich erreicht werden kann.
Dies liegt daran, dass die Widerstände entlang jeder endlosen Wegs zum Unendlichen aufsummiert werden, was zu einem unendlich großen Widerstand führt. Somit stellt sich die Frage, wo der eingespeiste Strom tatsächlich hinfließt. Dieses Paradoxon wird häufig mit der Annahme einer Erdung im Unendlichen erklärt. Streng genommen ist diese Annahme allerdings problematisch, denn ein Unendlich entfernen liegendes Erdungspotential ist mathematisch in der modellierenden Darstellung nicht wirklich definiert. Die unendliche Ausdehnung des Gitters hat daher weitere physikalische und mathematische Implikationen.
So wird häufig ein Grenzprozess betrachtet, in dem man die Größe eines endlichen, aber wachsenden Widerstandsnetzes erhöht und dabei beobachtet, wie sich die Widerstandswerte an den Knoten entwickeln. Die Ergebnisse deuten darauf hin, dass sich die Zahlenwerte für den äquivalenten Widerstand stabilisieren und somit eine Art asymptotisches Verhalten existiert, das der idealisierten Annahme eines unendlichen Gitters entspricht. Mathematisch wird das Problem häufig mit Hilfe von Differenzengleichungen beschrieben. Die Spannung an einem Knoten (m,n) hängt dabei linear von den Spannungen der benachbarten Knoten ab und eine natürliche Formulierung des Problems führt zu einer zweidimensionalen diskreten Laplace-Gleichung. Die Eigenwertanalyse der zugehörigen Gleichungen führt zu einer Lösungsform, die Produktionen von Potenzen komplexer Zahlen oder, alternativerweise, trigonometrische Funktionen umfasst.
In dieser Darstellung wird die Spannung als Fourier-Integral über Parameter geschrieben, die einer kontinuierlichen Reihe von Moden entsprechen. Für spezielle Punktpaare im Gitter, etwa benachbarte Knoten oder solche entlang einer Diagonale, lassen sich die Integrale analytisch oder numerisch auswerten, um genaue Werte für den Widerstand zu erhalten. Dabei zeigen sich elegante Symmetrien und Beziehungen zwischen den Werten, die beispielsweise durch bekannte Identitäten trigonometrischer Funktionen und kontinuierlicher Summen abgeleitet werden können. Neben der theoretischen Schönheit hat das unendliche Widerstandsnetz auch praktische Bedeutungen. In der Elektrotechnik dient das Modell als abstrakte Repräsentation für das Verhalten von Netzwerken aus vielen verschiedenen Bauteilen, bei denen eine genaue Modellierung sonst zu aufwendig wäre.
Förderung der Intuition für Potentialverteilungen in komplexen leitfähigen Materialien oder Berechnung von Fehlerströmen in großflächigen Schaltungen sind nur einige Anwendungen. Außerdem findet das Modell Beachtung in der Physik, insbesondere bei der Analyse von Zufallsprozessen auf Gittern, wie etwa dem sogenannten Random Walk, bei dem die Wahrscheinlichkeit eines Teilchens untersucht wird, das in einem Netz springt. Die Konnektivität des Gitters und die Art der Widerstände beeinflussen dabei die Bewegung und die Wahrscheinlichkeiten der Teilchenbewegungen. Daraus ergeben sich Verknüpfungen mit der Statistik und probabilistischen Methoden. Das Problem des unendlichen Widerstandsnetzes wurde im Lauf der Jahrzehnte von vielen Wissenschaftlern aus unterschiedlichsten Richtungen untersucht.
Direkte experimentelle Verifikation ist schwierig, weil ein physikalisch unendliches System natürlich nicht gebaut werden kann. Dennoch sind Computersimulationen mit sehr großen, aber endlich umfangreichen Netzen heute verbreitet. Diese ermöglichen es, das asymptotische Verhalten zu untersuchen und numerische Werte für verschiedene Abstände zwischen Knoten zu bestimmen. In der modernen Forschung sind Variationen des Problems ebenfalls von Interesse. Beispielsweise wird betrachtet, was passiert, wenn die Widerstände nicht alle gleich sind, sondern zufällig verteilt oder sich nach einem bestimmten Muster verändern.
Auch die Erweiterungen auf dreidimensionale Gitter oder andere Netzwerk-Geometrien werden erforscht. Diese komplexeren Fälle führen zu zahlreichen neuen Herausforderungen und erweitern das Anwendungsgebiet des Modells. Zu den mathematischen Techniken, die bei der Analyse solcher Netzwerke zum Einsatz kommen, gehören neben der Differenzengleichungen und Fourier-Transformation auch die Verwendung von Potentialtheorie, analytischen Funktionen, sowie numerischen Methoden zur Lösung großer Gleichungssysteme. Die Rolle von symmetrischen Eigenschaften und spezieller Funktionen ist dabei zentral, um Lösungen auszudrücken oder zu vereinfachen. Trotz der Komplexität lässt sich für das klassische unendliche quadratische Gitter der Widerstand zwischen zwei Knoten mit genügend Geduld und mathematischen Werkzeugen bestimmen.
Das Ergebnis R/2 zwischen direkt benachbarten Knoten ist ein elegantes Beispiel für den Zusammenhang zwischen unendlichen Strukturen und ihren lokalen Eigenschaften. Abschließend zeigt das unendliche Widerstandsnetz, dass zwischen physikalischer Intuition und mathematischer Strenge gelegentlich eine Kluft liegt. Das Modell lädt dazu ein, sich mit Grundlagenfragen des Stromflusses, der Potentialverteilung und der Grenzen idealisierter Systeme intensiver auseinanderzusetzen. Zugleich illustriert es, wie ein scheinbar triviales Netzwerk aus Tausenden und Millionen einfacher Widerstände ein komplexes und faszinierendes Konstrukt bilden kann, welches viele Bereiche der Wissenschaft miteinander verbindet.