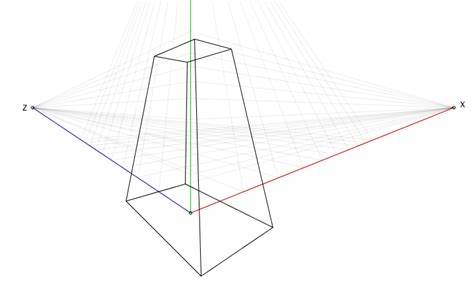
Die Dreipunktperspektive ist eine der faszinierendsten Methoden, um dreidimensionale Objekte und Räume auf einer zweidimensionalen Fläche darzustellen. Sie setzt sich aus drei Fluchtpunkten zusammen, die jeweils eine der Raumachsen repräsentieren. Während viele Tutorials die Dreipunktperspektive grob mit der simplen Verwendung eines 3D-Kamerasystems gleichsetzen, steckt hinter der strengen Umsetzung weit mehr Komplexität und kreative Möglichkeiten. Besonders wenn man diesen Ansatz streng nimmt und über die klassischen Darstellungen hinausgeht, lassen sich ungewöhnliche und spannende visuelle Effekte erzeugen, die das Verständnis von Perspektive und Raum herausfordern und bereichern können. Traditionell wird die Perspektive im Kunstunterricht und bei der Konstruktion von Zeichnungen auf dem Papier über Fluchtpunkte definiert.
Diese Punkte markieren den Ort, an dem parallele Linien im Raum scheinbar zusammenlaufen. Im Fall der Dreipunktperspektive treffen Fluchtlinien der X-, Y- und Z-Achsen in unterschiedlichen Punkten auf der Zeichenebene zusammen. Die Herausforderung liegt dabei darin, dass diese Fluchtpunkte im strengen Sinn im Unendlichen liegen. Das ist ein Konzept, das sich bei kleinen Zeichnungen noch gut handhaben lässt, jedoch in der computergrafischen Umsetzung auf Probleme stößt. Denn klassische 3D-Engines arbeiten mit linearer Algebra und planen Kamera-Modelle, bei denen die Abbildung von Weltraumkoordinaten auf die Bildschirmkoordinaten durch Matrizenmultiplikationen effizient erfolgt.
In echter Dreipunktperspektive jedoch stellen die Fluchtpunkte wirklich unendlich weit entfernte Punkte dar, was bedeutet, dass eine lineare Abbildung nicht mehr ausreicht. Die Folge ist, dass herkömmliche Rechenmethoden versagen, und kreative Alternativansätze gefragt sind. Interessant wird es, wenn man sich mit den zugehörigen mathematischen Funktionen zur perspektivischen Abbildung auseinandersetzt und begreift, wie man den Raum so transformiert, dass diese „Unendlichkeiten“ sinnvoll darstellbar bleiben und gleichzeitig Linien gerade bleiben. Eine Basis für das Verständnis bildet zunächst die Zweipunktperspektive, die durch zwei Fluchtpunkte auf der Horizontlinie definiert wird. In der praktischen Umsetzung auf Papier benötigt man häufig einen sogenannten „Zero Point“ als Bezugspunkt, der beim Programmieren unabdingbar wird, da für den Computer exakte Positionen und Höhen bestimmt werden müssen.
Die Höhe dieses Punktes über der Bodenlinie legt die Perspektive fest und erlaubt eine korrekte Zuordnung von 3D-Punkten auf die Projektionsebene. Das Koordinatensystem bei der perspektivischen Abbildung ist indes kein einfaches Gitter, wie man es von ortogonal ausgerichteten Systemen kennt, sondern vielmehr eine verzerrte Fläche, die den Bereich zwischen den Fluchtpunkten in sich zusammenzieht. Diese Verzerrung zeigt sich darin, dass die Punkte auf der Zeichenfläche eine zunehmende Dichte in der Nähe der Fluchtpunkte aufweisen. Was man dabei konstatieren kann, ist, dass nicht einfach ein Rechteck mit zusammengezogenen Kanten abstrahiert wird, sondern ein komplexes Polygon, dessen Diagonalen selbst unendlich viele Koordinatenpunkte zusammenfassen – sogenannte “Linien von Unendlichkeiten”. Ein großer Teil des erfolgreichen Mapping-Prozesses von 3D- zu 2D-Koordinaten liegt in der Funktion zur Berechnung der Distanzverhältnisse.
Mit Hilfe von Linearinterpola- tionen (Lerp) lassen sich Entfernungen zwischen definierten Punkten auf der Zeichenebene zwischen 0 und 1 normieren. Dies erlaubt eine einfachere Handhabung von Positionen in Grafiken, insbesondere wenn man weiß, wie Werte von – unendlich bis unendlich – in einen fixen Intervall transformiert werden können. Frühe Versuche nutzten zur Transformation der Koordinaten exponentielle Funktionen. Diese haben jedoch den gravierenden Nachteil, dass sie parallele Linien zu Krümmungen verfälschen, was bei der strengen Dreipunktperspektive nicht tolerierbar ist. Linien sollen auch in der perspektivischen Abbildung gerade bleiben, um das dreidimensionale Raumverständnis nicht zu beeinträchtigen.
Die Analyse und visuelle Überprüfung von verschiedenen Linienmustern zeigte deshalb, dass exponentielle Mappings unbrauchbar sind. Eine wesentlich bessere Alternative ist ein rationaler Mapping-Ansatz anhand multiplikativer Inversen, der zwar bei negativen Werten eine Asymptote besitzt, aber in den wichtigen Bereichen für positive Werte eine äußerst geradlinige und präzise Transformation ermöglicht. Dieser Trick erlaubt es, den für den Betrachter sichtbaren Raum gut zu definieren und gleichzeitig Verzerrungen zu vermeiden, indem Bettpunktbereiche, die hinter dem Betrachter liegen würden, konsequent ausgeblendet werden können. Das sogenannte Culling ist ein wichtiger Bestandteil, um Artefakte zu vermeiden, wenn Bereiche der Geometrie in diese problematischen Zonen hineinragen. Im praktischen Programmieralltag wird daher meist entsprechend ein Offset verwendet, der die Szene so verschiebt, dass alles Wesentliche vor der Asymptote liegt.
Das ist eine pragmatische und effektive Lösung, die einfach implementierbar ist und zuverlässige Resultate liefert. Für die eigentliche Projektion von 3D-Koordinaten in das zweidimensionale Bild benötigt man eine Reihe von Funktionselementen. Dazu zählt das Ebenen-Mapping mithilfe von linearen Interpolationen entlang der Achsen, das Berechnen von Schnittpunkten zweier Linien und die Verwendung spezieller Scalingfaktoren für unterschiedliche Achsen, insbesondere in der Dreipunktperspektive, in der auch die vertikale Achse ein Fluchtpunkt ist. Die Erweiterung vom zweidimensionalen zum dreidimensionalen Mapping ist weniger eine neue Methode, als vielmehr eine Erweiterung der vorhandenen Logik. Anstelle nur zwei Fluchtpunkte und die Bodenlinie zu berücksichtigen, wird zusätzlich der vertikale Fluchtpunkt eingefügt.
Das bedeutet, dass Dreidimensionalität vollständig in die Perspektivenberechnung mit einfließt und alle Raumrichtungen realistisch verzerrt werden. Das führt zu den charakteristischen „pointy“ Effekten, bei denen alle vertikalen Linien nicht mehr parallel dargestellt werden, sondern konvergieren. In der Praxis steuert man den Grad der Verzerrung durch verschiedene Skalierungsfaktoren. So kann man gezielt steuern, wie stark die Dehnung in Höhenrichtung ausfällt. Dieses Feintuning gibt dem Entwickler und Künstler interessante Freiheiten, die kommerziellen 3D-Softwarelösungen oft so nicht bieten.
Es lässt sich so insbesondere künstlerisch umgesetzt eine sehr dynamische und expressive Bildwirkung erzeugen. Darüber hinaus zeigt die Untersuchung möglicher Mapping-Funktionen auch, welche Auswirkungen eine missglückte Wahl nach sich zieht. Die ursprünglich intuitive Wahl einer exponentiellen Funktion führt zu frappierenden Verzerrungen, sobald die Objekte im Raum gedreht oder perspektivisch verschoben werden. Gerade dort entlarven sich vor allem die „gekörnten“ Linien, die eigentlich gerade sind, als ungewollte Kurven. Für experimentelle Animationen kann so etwas zwar reizvoll sein, im professionellen Kontext reduziert dies jedoch meist die Qualität der Darstellung.
Die komplexe Beschäftigung mit der korrekten Implementierung der Dreipunktperspektive unterstreicht mehr als alles andere, wie leicht Begeisterung für ein gestalterisches Konzept mit den mathematischen Grundlagen kollidieren kann. Eine tiefere Auseinandersetzung fördert jedoch ein Verständnis dafür zu Tage, wie Perspektive mehr als nur eine technische Darstellung ist, sondern eine kreative Sprache des Raumes und der Wahrnehmung. Während die Vorteile eines Musikstücks oder eines Meisterwerks häufig intuitiv erfassbar sind, sind die Herausforderungen einer echt umgesetzten Dreipunktperspektive zuerst mathematischer und technischer Natur – doch gerade dort liegt auch eine besondere Chance. Die Fähigkeit, durch eigenentwickelte Algorithmen jenseits gedachter Grenzen darstellbar zu machen, eröffnet neue visuelle Möglichkeiten und erweitert die künstlerische und technische Toolbox. Die Dreipunktperspektive lebt von der Balance zwischen physikalischer Realität und künstlerischer Freiheit.