Vertrauensintervalle sind ein zentrales Konzept der Statistik, das es erlaubt, mit unvollständigen Informationen eine Einschätzung über unbekannte Größen zu gewinnen. Sie sind grundlegend für das Verständnis von wissenschaftlichen Ergebnissen sowie für Entscheidungen in Wirtschaft, Medizin und vielen anderen Bereichen. In einer Welt, in der selten alle Daten eines gesamten Phänomens vorliegen, liefert das Vertrauensintervall einen Bereich, der mit einer bestimmten Sicherheit den tatsächlichen Wert der untersuchten Größe abdeckt. Dieses Vorgehen schafft Klarheit und Vertrauen, auch wenn man niemals die exakte Antwort kennt. Die Anwendung von Vertrauensintervallen ist daher unverzichtbar beim Umgang mit Stichprobendaten, denn sie zeigt auf, wie verlässlich eine Schätzung ist und welche Spanne von möglichen Werten realistisch erscheint.
Um die Bedeutung von Vertrauensintervallen zu verstehen, hilft ein einfaches Beispiel: Stellen Sie sich vor, Sie möchten wissen, wie viele Pizzastücke eine Person in 30 Minuten essen kann. Es wäre unpraktisch und teuer, jeden Menschen auf der Welt dazu zu befragen oder zu testen. Stattdessen nimmt man eine Stichprobe einer begrenzten Anzahl Personen und misst deren durchschnittliche Verzehrmenge. Dieser Durchschnittswert ist jedoch nur eine Annäherung an die Realität, denn jede Stichprobe bringt durch die zufällige Auswahl der Teilnehmer Schwankungen mit sich. Vertrauensintervalle helfen dabei einzuschätzen, wie genau dieser Mittelwert ist und in welchem Bereich der wahre Durchschnitt wahrscheinlich liegt.
Die zentrale Voraussetzung für eine verlässliche Nutzung von Vertrauensintervallen ist die Zufallsauswahl der Stichprobe. Nur wenn jede Person der Grundgesamtheit die gleiche Chance hat, in die Stichprobe zu gelangen, kann man Verzerrungen und systematische Fehler vermeiden. Ohne Zufallsauswahl drohen Fehlschlüsse und damit falsche Entscheidungen. Doch selbst bei perfekter Zufallsauswahl ist es möglich, dass eine einzelne Stichprobe ein ungewöhnliches Ergebnis zeigt, etwa weil zufällig viele Menschen mit besonders großem Appetit ausgewählt wurden. Solche Ausreißer sind selten, da die meisten Stichprobenwerte dazu neigen, sich um den wahren Wert zu gruppieren, was wiederum das Vertrauen in die Methode stärkt.
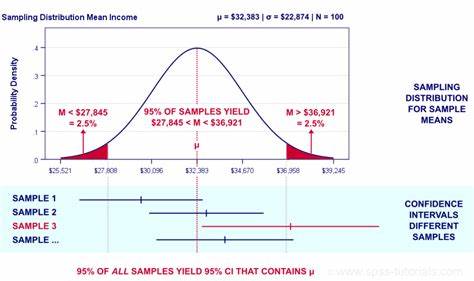
Dieses Verhalten der Stichprobenmittelwerte folgt einem fundamentalen Prinzip der Statistik, dem sogenannten Zentralen Grenzwertsatz. Er besagt, dass wenn man viele Stichproben aus einer Grundgesamtheit zieht und deren Mittelwerte berechnet, sich die Verteilung dieser Mittelwerte einer Normalverteilung annähert – also einer glockenförmigen, symmetrischen Kurve. Das ist bemerkenswert, denn auch wenn die Verteilung der einzelnen Datenpunkte stark verzerrt und unregelmäßig ist, zeigen die Mittelwerte ein viel berechenbareres Muster. Diese Eigenschaft ermöglicht es, mit statistischen Methoden genaue Vorhersagen zu treffen und Vertrauensgrenzen um Schätzwerte zu ziehen. Die Breite eines Vertrauensintervalls hängt von mehreren Faktoren ab.
Einerseits spielt die Streuung der Messwerte in der Grundgesamtheit eine Rolle: Je größer die Unterschiede innerhalb der Bevölkerung sind, desto größer kann die Abweichung des Stichprobenmittelwerts vom tatsächlichen Mittelwert sein. Andererseits beeinflusst die Größe der Stichprobe die Genauigkeit der Schätzung: Je mehr Personen in der Stichprobe sind, desto geringer ist die Schwankungsbreite des Mittelwerts, da Ausreißer durch die größere Zahl an Datenpunkten ausgeglichen werden. Diese beiden Elemente bestimmen gemeinsam den sogenannten Standardfehler, der das Maß für die typische Abweichung des Stichprobenmittels vom wahren Wert darstellt. Das Vertrauensintervall selbst wird durch Multiplikation des Standardfehlers mit einem Faktor gebildet, der von dem gewünschten Vertrauensniveau abhängt. Häufig werden 95 Prozent als Standard gewählt: Das bedeutet, dass bei wiederholter Durchführung der Stichproben und Berechnung der Vertrauensintervalle etwa 95 von 100 dieser Intervalle den wahren Wert enthalten.
Diese Aussage ist zwar gegenständlich schwer zu fassen, aber sie stellt die statistische Grundlage dar, auf der man seine Unsicherheit quantitativ beschreiben kann. Es ist wichtig zu verstehen, dass ein einzelnes berechnetes Intervall entweder den wahren Wert enthält oder nicht; das Vertrauensniveau beschreibt vielmehr die Zuverlässigkeit des Verfahrens, mit dem das Intervall ermittelt wurde. Die Interpretation von Vertrauensintervallen hat im Alltag und in der Forschung weitreichende Bedeutung. Wer Ergebnisse aus Studien oder Analysen betrachtet, sollte nach Möglichkeit immer auf Angabe von Vertrauensintervallen achten, da sie eine Einschätzung der Aussagekraft liefern. Ein Mittelwert ohne Angabe, wie genau er geschätzt wurde, kann trügerisch sein.
Ein enges Vertrauensintervall signalisiert hohe Genauigkeit und damit eine bessere Grundlage für Entscheidungen, während ein sehr breites Intervall eher warnt, dass die Schätzung unsicher ist und weitere Untersuchungen oder größere Stichproben nötig sein könnten. Allerdings gibt es auch eine Balance zu beachten: Je größer das Vertrauen, das man in die Aussage einfordert, desto breiter wird das Intervall. Es ist also nicht zielführend, einfach ein extrem hohes Konfidenzniveau zu wählen, da dies oft zu sehr vagen Ergebnissen führt, die wenig nützen. Vielmehr muss man je nach Anwendungsfall abwägen, wie viel Unsicherheit akzeptabel ist und welches Vertrauensniveau sinnvoll erscheint. In der Praxis haben sich 90, 95 oder 99 Prozent durchgesetzt, doch auch andere Werte sind möglich und unter bestimmten Voraussetzungen gerechtfertigt.
Darüber hinaus illustriert eine anschauliche Metapher die Logik hinter dem Vertrauensintervall besonders gut. Man kann sich vorstellen, dass ein Junge und sein Hund gemeinsam durch die Nachbarschaft spazieren. Der Junge repräsentiert den wahren Wert, der uns verborgen bleibt, während der Hund den beobachteten Stichprobenmittelwert symbolisiert, der sich um den Jungen bewegt und manchmal weiter entfernt ist. Wenn wir den Hund sehen, können wir anhand seines typischen Bewegungsmusters eine Schätzung abgeben, wo sich der Junge befindet. Diese Schätzung ist in Form eines Vertrauensintervalls der Bereich, in dem wir glauben, den Jungen zu finden, selbst wenn wir ihn nicht direkt sehen können.
So helfen uns Vertrauensintervalle, auf Basis der begrenzten Daten die verborgene Realität besser zu verstehen. Vertrauensintervalle sind nicht nur abstrakte theoretische Konstrukte, sondern finden in vielfältigen Bereichen Anwendung. In der Medizin dienen sie dazu, die Effektivität neuer Therapien zu bewerten. Bei Wahlumfragen erlauben sie eine Einschätzung der zu erwartenden Stimmanteile. Auch in der Qualitätskontrolle von Produkten oder bei Wirtschaftsdaten sind sie unverzichtbar, um Aussagen über die Gesamtpopulation auf Basis von Stichproben zu treffen.
Ebenso helfen sie Unternehmen dabei, Entscheidungen zu treffen, die auf Marktforschung beruhen, und das Risiko von Fehlentscheidungen zu minimieren. Die Berechnung von Vertrauensintervallen kann bei großen und komplexen Datenmengen herausfordernd sein, weshalb Statistiksoftware und Programmiersprachen wie R, Python oder spezialisierte Tools häufig eingesetzt werden. Moderne Methoden erlauben darüber hinaus auch die Berücksichtigung von weiteren Unsicherheiten und komplexeren Modellen, wodurch die Aussagekraft und Genauigkeit weiter verbessert werden kann. Dennoch bleibt das Grundprinzip stets das gleiche: Ein Vertrauensintervall gibt Auskunft darüber, in welcher Spanne der wahre Wert mit einer gewissen Sicherheit liegt. In einer Zeit, in der Daten eine immer größere Rolle spielen, ist das Verständnis von Vertrauen und Unsicherheit unverzichtbar.
Vertrauensintervalle leisten dabei einen grundlegenden Beitrag, um aus Stichprobendaten verlässliche Erkenntnisse zu gewinnen. Sie helfen dabei, Bauchgefühl durch fundierte statistische Methoden zu ersetzen und sichern Entscheidungen durch eine transparente Darstellung der Unsicherheiten ab. Wer mit Daten arbeitet, sollte dieses Werkzeug daher nicht nur kennen, sondern auch gezielt einsetzen, um die Qualität und Glaubwürdigkeit seiner Analysen zu steigern. Abschließend bleibt festzuhalten, dass Vertrauensintervalle nicht nur mathematische Konstrukte sind, sondern ein Ausdruck für einen verantwortungsbewussten Umgang mit Wissen aus begrenzten Informationen. Sie öffnen einen Weg, der zwischen Zuversicht und Vorsicht balanciert und es ermöglicht, trotz Ungewissheit fundierte Aussagen zu treffen.
Wer die Logik und Bedeutung von Vertrauensintervallen verinnerlicht, gewinnt eine solide Grundlage, um komplexe Situationen besser zu verstehen und auf Basis von Daten bewusste, durchdachte Entscheidungen zu treffen.