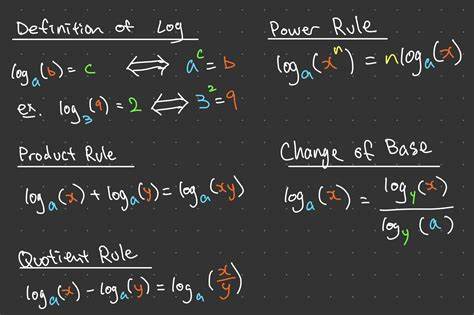In der Welt der Softwareentwicklung sind Zahlenverarbeitung und deren effiziente Darstellung essenzielle Themen. Besonders bei der Umwandlung von Zahlen in ihre Zeichenketten-Darstellung, der Berechnung der Anzahl der Ziffern oder bei mathematischen Operationen wie dem Logarithmus zur Basis 10 (log10) spielen sowohl Performance als auch Korrektheit eine zentrale Rolle. Wer sich schon einmal gefragt hat, wie oft eine Applikation Zahlendarstellungen vornimmt oder wie viele Ziffern ein bestimmter Wert hat, stößt unweigerlich auf das Problem, exakte und schnelle Methoden zur Berechnung dieser Werte zu finden – und dies für unterschiedlichste Datentypen von 8-Bit-Integern bis hin zu 64-Bit-Gleitkommazahlen. Im Folgenden werden tiefgehende Einblicke in die Mechaniken, Herausforderungen und Lösungsansätze rund um Strings, Exponenten und log10 präsentiert. Dabei werden auch praktische Beispiele aus der .
NET-Umgebung herangezogen, deren Prinzipien jedoch universelle Gültigkeit besitzen und leicht für andere Programmiersprachen adaptiert werden können. Eine der zentralen Fragestellungen in der Zahlenthematik innerhalb der Informatik ist die Bestimmung der Anzahl der Dezimalstellen einer Zahl. Auf den ersten Blick scheint dies trivial: Man könnte die Zahl wiederholt durch 10 teilen, bis das Ergebnis null ist, und dabei die Anzahl der Divisionen zählen. Alternativ kommt die mathematische Erkenntnis ins Spiel, dass die Anzahl der Ziffern sich über den Logarithmus zur Basis 10 bestimmen lässt. Konkret gibt der ganzzahlige Anteil von log10(x) + 1 die Menge der Ziffern an.
Hier kommen jedoch unterschiedliche Herausforderungen ins Spiel. Die direkte Realisierung durch Logarithmusfunktionen ist zwar mathematisch elegant, aber performance-technisch nicht optimal, da sie oft den kompletten log10-Wert inklusive des ungenutzten Nachkommateils berechnet und Floating-Point-Berechnungen innewohnt, die relativ teuer sind. Insbesondere in Performance-kritischen oder embedded Systemen, in denen Rechenzeit und Speicher limitiert sind, zählt jede Optimierung. Die meisten populären Prozessoren, die x86- oder ARM-Befehlssätze verwenden, besitzen keine dedizierten Hardwarebefehle zum direkten Berechnen von log10. Stattdessen gibt es meist Hardwareanweisungen für log2 oder andere mathematische Grundoperationen, von denen log10 dann in Software mittels Umrechnungen abgeleitet wird.
Dies führt zwangsläufig zu Overhead und oft unnötigem Rechenaufwand, besonders wenn nur die ganzzahlige Stellenanzahl benötigt wird. Für Ganzzahlen unterschiedlicher Bitbreite gestaltet sich das Problem vielseitig. Eine 8-Bit-Zahl bewegt sich zwischen 0 und 255, also zwischen einer und drei Dezimalstellen. Für 16-Bit Zahlen im Bereich von 0 bis 65.535 sind es bis zu fünf Ziffern, bei 32-Bit-Werten bis zu zehn und bei 64-Bit sogar bis zu zwanzig Ziffern.
Ein einfacher Software-Ansatz, der beispielsweise für 8-Bit-Werte zum Einsatz kommt, sieht wie folgt aus: Man vergleicht diese Zahl mit Schwellenwerten wie 10 und 100 und kann so effizient die Ziffernanzahl ermitteln, indem man nur maximal zwei oder drei Vergleiche durchführt. Das Problem bei solchen Vergleichen sind allerdings mögliche Prozessorzweigvorhersagefehler (Branch Mispredictions), die in modernen Hochleistungsprozessoren kostspielig sein können und somit die Performance stark beeinträchtigen können. Dies fordert eine Neuüberlegung, wie sich solche Vergleiche strukturieren lassen, um möglichst wenige oder gar keine Verzweigungen zu nutzen. Untersuchungen zeigen auch, dass gängige Lösungen wie das Umwandeln der Zahl in einen String und das Bestimmen der Länge der Zeichenkette oft effizienter sind, als man vermuten würde. Insbesondere bei .
NET profitiert man hier von interner String-Caching-Mechanik, welche kleine Zahlen in Form von Strings zwischenspeichert und somit schnelle Zugriffe ohne neue Speicherallokationen ermöglicht. Dies illustriert die Tatsache, dass tiefgehende Optimierungen und langjährige Entwicklungsbemühungen in Frameworks maßgeblich die Performance beeinflussen können. Die DigitCount-Funktion in modernen Laufzeitumgebungen wie .NET zeigt eine interessante Herangehensweise, bei der neben Vergleichen auch Bit-Operationen zum Einsatz kommen. Ein häufig verwendetes Verfahren basiert auf dem Bestimmen des Logarithmus zur Basis 2 (log2), einer Operation, die oft durch spezielle Befehle wie LZCNT (Leading Zero Count) hardwaregestützt und somit extrem schnell abgewickelt wird.
Anhand des errechneten log2 lässt sich mit Hilfe von Lookup-Tabellen und ein wenig Arithmetik die Anzahl der Dezimalziffern präzise und performant bestimmen. Dabei werden sogenannte magische Zahlen (magic numbers) verwendet, die gewährleisten, dass das Ergebnis mathematisch korrekt für jeden möglichen Input ist. Weiterhin kann durch Parallelisierung der Vergleichsoperationen und eine geschickte Reduzierung von Abhängigkeiten zwischen Bedingungen die Leistung optimiert werden. Allerdings zeigen Benchmarks, dass eine vollständige Eliminierung von Zweigen mittels Parallelvergleich tatsächlich aufgrund des stark angestiegenen Vergleichs- und Rechenaufwands in der Software um ein vielfaches langsamer sein kann als die native Umsetzung im Standardbibliothek-Code, der mit internen Optimierungen und Maschinencode auf niedrigster Ebene arbeitet. Bei 64-Bit-Integern entsteht noch eine weitere Herausforderung aufgrund des enormen Wertebereichs.
Hier werden häufig Techniken verwendet, bei denen die Zahl über Schwellenwerte in Segmente zerlegt wird – beispielsweise prüft man, ob die Zahl größer als 10 Milliarden ist, um dann die Anzahl der Ziffern in zwei Schritten zu bestimmen. Solche Rekursionen oder Segmentierungen erlauben einen Kompromiss zwischen Code-Komplexität und Ausführungszeit. Dennoch liegt die Performance solcher Eigenlösungen meist immer noch hinter den Implementierungen der standardisierten Bibliotheken zurück. Ein kritischer Aspekt, der nicht außer Acht gelassen werden darf, ist der Einfluss von Branch Mispredictions. Bei zufälligen und variierenden Zahlen führt häufiges Springen zwischen unterschiedlichen Pfaden in der Ausführung dazu, dass die CPU-Optimierungen zur Vorhersage von Befehlen versagen und stattdessen Zeit durch Ausführen falscher Pfade verloren geht.
Besonders in Szenarien, in denen viele Zahlen unterschiedlicher Größen verarbeitet werden, zeigt sich dieser Effekt deutlich. Daher ist die Minimierung solcher Verzweigungen beziehungsweise der Einsatz von Techniken, welche die Zweigabhängigkeiten reduzieren oder eliminieren, ein zentrales Thema für Performanceoptimierungen. Die Probleme und Lösungen setzen sich bei Gleitkommazahlen fort, die noch komplexere Strukturen mit Mantisse und Exponent aufweisen. Gerade im wissenschaftlichen Rechnen oder in der Implementierung von großen wissenschaftlichen Datentypen ist es essenziell, schnell und genau den ganzzahligen Teil des log10 eines Gleitkommawerts zu erhalten, um etwa Normierungsschritte in der Darstellung durchführen zu können. Dies ist beispielsweise relevant für die Darstellung von Zahlen im wissenschaftlichen Format M x 10^E, wobei M die Mantisse und E der Exponent ist.
Für Gleitkommazahlen gibt es kaum hardwaregestützte Anweisungen für log10. Stattdessen wird meistens über Standardbibliotheksfunktionen wie Math.Log10 gearbeitet, deren Kosten für einfache Operationen relativ hoch sind. Eine Alternative ist eine Kombination aus pragmatischen, schwellenwertbasierten Konditionen und klassischem Logarithmus. Durch Vergleiche mit potenziellen Exponentenbereichen wird zuerst ein grobes Resultat bestimmt, bevor im Bedarfsfall die präzise, aber teurere log10-Berechnung aufgerufen wird.
Dies erspart in vielen Fällen teure Operationen und verbessert die Performance drastisch. So werden beispielsweise Werte unter einem Schwellenwert, etwa 1e9, zunächst durch einfache Vergleichsoperationen in Kategorien eingeordnet. Diese Kategorien entsprechen etwa der Anzahl der Ziffern und erlauben ein schnelles Abschätzen des Logarithmus. Für extrem kleine Werte werden ähnliche Techniken angewendet, um negative Exponenten abzudecken. Durch solche auf Schwellenwerten basierten Implementierungen, häufig realisiert durch verschachtelte ternäre Operationen oder Switch-Ausdrücke je nach verwendeter Programmiersprache, wird bei der Berechnung des ganzzahligen Anteils des Logarithmus eine enorme Performanceverbesserung erreicht.
Zwar leidet die Lesbarkeit solcher Konstrukte oft – insbesondere wenn sie lang sind und viele Stufen enthalten –, doch die tatsächliche Ausführungsgeschwindigkeit zählt in vielen Szenarien mehr als der ästhetische Code. In Benchmarks zeigt sich, dass diese Mischimplementierungen mit einfacher Logik signifikant schneller als reine Aufrufe von Math.Log10 sind und sich gut für den täglichen Gebrauch eignen, wenn Zeit kritische Anwendungen berücksichtigt werden müssen. Dabei fällt auch auf, dass die Wahl der Vergleichsreihenfolge und der verwendeten Schwellenwerte den größten Einfluss auf das Ergebnis hat. Ein spannender Aspekt, der in der Forschung und Entwicklung noch weiter verfolgt werden kann, ist die Verwendung von Lookup-Tabellen und sogenannter Magic-Number-Techniken auch für Gleitkommazahlen.
Da der Binäre Exponent in der IEEE-754-Darstellung schnell auslesbar ist, lässt sich das Logarithmusergebnis mithilfe von vordefinierten Werten transformieren. Die Erstellung solcher Tabellen und die Implementierung der entsprechenden Funktionen können noch in zukünftigen Frameworks zu deutlichen Performancegewinnen führen. Im Gegensatz zu Integern, bei denen solche Methoden schon weit verbreitet sind, ist das im Bereich von Fließkommazahlen noch ein recht junges Forschungsfeld. Zusammenfassend lässt sich sagen, dass die effiziente Berechnung der Anzahl der Dezimalziffern oder des ganzzahligen Logarithmus zur Basis 10 ein komplexes Problem mit vielen Facetten ist. Hardwareunabhängig dominieren softwareseitige Optimierungen und clever programmierte Implementierungen den Markt.
Dabei können naheliegende Methoden, wie vollständige String-Konvertierungen oder einfache Logarithmus-Aufrufe, in modernen Runtimeumgebungen mit zahlreichen Optimierungen in der Regel nicht so leicht geschlagen werden. Trotzdem haben im speziellen Anwendungsbereich maßgeschneiderte Funktionen ihre Berechtigung, vor allem dann, wenn Zweigvorhersagefehler ein kritischer Flaschenhals sind oder die Vermeidung temporärer Ressourcen wie Strings erwünscht ist. Die Fortschritte der letzten Jahre zeigen neue Wege auf, wie man mit einfachen Mitteln, basierend auf Bitoperationen, Lookup-Tabellen und verzweigungssparenden Konstrukten, ideale Performance erreichen kann. Diese Entwicklungen fördern zudem ein besseres Verständnis der zugrundeliegenden Hardwarearchitekturen, ermöglichen die optimale Nutzung vorhandener Befehle und legen den Grundstein für zukünftige Erweiterungen auf Prozessor-Seite. Für jeden Entwickler, der sich mit Zahlenrepräsentation, sehr großen Zahlen oder High-Performance-Computing beschäftigt, lohnt sich daher ein tieferer Blick in das Zusammenspiel von Strings, Exponenten und log10.
Die damit verbundenen Herausforderungen, wie branch mispredictions, fehlende Hardwarebefehle für bestimmte mathematische Zwecke und die Balance zwischen Klarheit und Geschwindigkeit, treiben Innovationen voran und sind wegweisend für die nächsten Generationen von Softwarebibliotheken auf verschiedenen Plattformen.