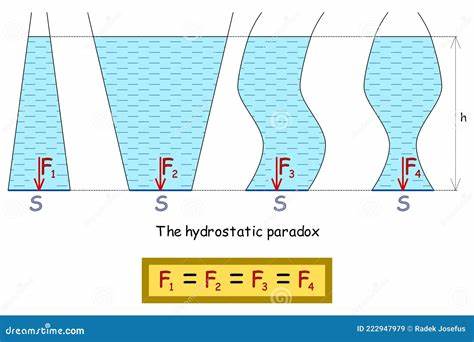
Das hydrostatische Paradoxon: Wie Flüssigkeiten ohne Widerspruch funktionieren

Das hydrostatische Paradoxon zählt zu den faszinierendsten Phänomenen in der Physik der Flüssigkeiten und verblüfft bis heute viele Menschen, die mit dem Verhalten von Wasser und anderen Flüssigkeiten nicht vertraut sind. Es beschreibt scheinbar widersprüchliche Beobachtungen, die sich ergeben, wenn Flüssigkeiten in Gefäßen mit unterschiedlich geformten Kammern und Verbindungen stehen. Obwohl das Thema vor Jahrhunderten erstmals formuliert wurde, bildet es bis heute eine wichtige Grundlage für unser Verständnis der Hydrodynamik und der Physik statischer Flüssigkeiten. Der Ursprung des hydrostatischen Paradoxons liegt im eigentlich einfachen, aber schwer intuitiv nachvollziehbaren Verhalten von Wassersäulen in miteinander verbundenen Gefäßen. Stellt man sich einen Behälter vor, der aus mehreren Kammern mit unterschiedlich großem Volumen, aber gleicher Grundfläche besteht, fällt eines sofort ins Auge: Die Wasserstände in allen Kammern gleichen sich aus.

Unabhängig davon, wie viel Wasser in die einzelnen Kammern gefüllt wird, erreicht das Wasser – sobald es zur Ruhe kommt – immer dieselbe Höhe in allen verbundenen Behältern. Dies wirkt paradox, denn man würde vermuten, dass der Boden der Kammer mit größerem Wasservolumen einen höheren Druck erfährt und somit auch in die anderen Kammern mehr Wasser „drücken“ müsste. Der französische Mathematiker und Physiker Blaise Pascal beschäftigte sich erstmals intensiv mit dieser Fragestellung vor beinahe 300 Jahren. Um das hydrostatische Paradoxon zu veranschaulichen, entwickelte er sogenannte „Pascalsche Vasen“. Diese bestehen aus mehreren miteinander verbundenen Behältern verschiedener Form und Größe, die alle eine gemeinsame Grundfläche besitzen, jedoch unterschiedlich hoch und weit geformt sind.

Pascal zeigte damit, dass der Wasserstand immer gleich bleibt, egal wie verschieden die Kammern geformt sind. Das scheinbare Paradoxon lässt sich mithilfe der grundlegenden Gesetze der Mechanik und Fluidstatik auflösen. Der Druck an einem bestimmten Punkt in einer ruhenden Flüssigkeit wird ausschließlich durch das Gewicht der darüber liegenden Flüssigkeitssäule bestimmt und ist unabhängig von der Form oder dem Volumen der Gefäße. Das heißt: Der Druck an der Basis der Kammer hängt ausschließlich von der Höhe der Wassersäule über diesem Punkt ab. Diese Erkenntnis lässt sich leicht nachvollziehen, wenn man überlegt, welche Kräfte auf das Wasser wirken.

Die seitlichen Wände eines Gefäßes drücken nicht direkt auf den Boden, sondern wirken seitlich auf die Flüssigkeit. Die vertikale Kraft, die den Boden belastet, resultiert einzig aus dem Gewicht der darüber stehenden Wassersäule. Die horizontalen Kräfte gleichen sich im Gleichgewicht aus, was dazu führt, dass die Flüssigkeitssäulen in allen Kammern dieselbe Höhe erreichen, um den Druck auszugleichen. Ein klassisches und sehr anschauliches Beispiel für das hydrostatische Paradoxon wird anhand von riesigen Staudämmen wie dem Hoover-Staudamm gegeben. Trotz der enorm unterschiedlichen Größe der dahinter stehenden Wasserflächen – zum Beispiel der riesigen Fläche des Lake Mead gegenüber einem hypothetisch viel kleineren Stausee – ist der horizontale Wasserdruck auf die dammbildende Fläche an einer bestimmten Wassertiefe überall gleich.

Dies hat viele Menschen verwundert, da intuitiv angenommen wird, dass mehr Wasser an einer größeren Wasserfläche automatisch auch mehr Druck erzeugen müsste. Doch die physikalische Realität ist anders. Da der Druck in einer Flüssigkeit nur von der Wassertiefe abhängt, ist der Druck an der Basis des Staudamms nicht von der Breite oder Länge des Seenbeckens abhängig, sondern von der Höhe der Wassersäule über dem Punkt. Diese Tatsache ist für Ingenieure und Bauplaner enorm wichtig, da der Staudamm so ausgelegt werden muss, dass er diesem maximalen Druck an der tiefsten Stelle standhält, unabhängig von der Gesamtwassermenge des Sees. Eine besonders einprägsame Demonstration dieses Prinzips bietet ein Versuchsaufbau mit einer flexiblen Membran, die zwei unterschiedlich große Wasserkammern voneinander trennt.

Füllt man Wasser in die größere Kammer, wölbt sich die Membran in die kleinere Kammer hinein. Wenn man Wasser in die kleinere Kammer nachfüllt, verringert sich die Verformung der Membran, bis die Wasserstände auf beiden Seiten identisch sind und die Membran wieder in ihrer ursprünglichen Form steht. Dieses Modell macht anschaulich, dass der Druck von der Höhe der Flüssigkeit und nicht vom Volumen abhängt. Das hydrostatische Paradoxon hat weitreichende Konsequenzen und spielt eine zentrale Rolle in verschiedenen Anwendungsgebieten. Zum Beispiel in der Schiffstechnik, beim Bau von Behältern oder in der Hydraulik, wo es für die Funktionsweise von hydraulischen Hebevorrichtungen und Bremsen von ausschlaggebender Bedeutung ist.

Die Druckübertragung durch Flüssigkeiten ist zuverlässig und vorhersagbar, was diese Technologien ermöglicht. Trotz seines zunächst paradoxen Erscheinungsbildes bestätigt das hydrostatische Paradoxon ein zentrales Prinzip der Physik: Der Druck in einem ruheverteilten Fluid wird allein durch die Höhe der Flüssigkeitssäule bestimmt, unabhängig von ihrer Form oder dem Gesamtvolumen. Es lehrt uns, dass Intuition bei der Betrachtung von physikalischen Systemen oft irreführend sein kann und dass nur der genaue Blick auf die zugrundeliegenden physikalischen Gesetze zu einem exakten Verständnis führt. Das Verständnis dieses Paradoxons ist auch ein hervorragendes Beispiel dafür, wie experimentelle Beobachtungen und theoretische Erklärungen zusammenkommen, um scheinbar widersprüchliche Phänomene zu entwirren. Es zeigt, wie wichtig es ist, sich von voreiligen Annahmen zu trennen und stattdessen zu präzisen Messungen und Berechnungen zu greifen.

Abschließend kann festgehalten werden, dass das hydrostatische Paradoxon kein Widerspruch der Physik ist, sondern ein Beleg für die konsistente und universelle Gültigkeit der Grundgesetze der Fluidstatik. Jede Flüssigkeit in Ruhe verhält sich nach den gleichen Prinzipien, unabhängig davon, ob sie sich in einer einfachen Vase, einem gigantischen Staudamm oder einem komplexen hydraulischen System befindet. Dieses Wissen ist nicht nur für Wissenschaftler, sondern auch für Techniker, Ingenieure und jeden, der sich mit Flüssigkeiten und Druck beschäftigt, von unschätzbarem Wert.