Die Welt der Mathematik und Signalverarbeitung hält einige faszinierende Verbindungen bereit, die auf den ersten Blick überraschend eng miteinander verknüpft sind. In einem besonderen Fokus stehen dabei die Multiplikation von Polynomen, das Konzept der diskreten Faltung und der Einsatz sogenannter umgekehrter Kerne. Diese scheinbar unterschiedlichen Gebiete sind durch gemeinsame Strukturen und Prinzipien verbunden, die sowohl theoretisch interessant als auch praktisch bedeutsam sind. Beginnen wir mit den Grundlagen der Polynom-Multiplikation, einer der grundlegendsten Operationen in der Algebra. Zwei Polynome miteinander zu multiplizieren, ist ein Verfahren, das bereits im Schulunterricht behandelt wird.
Dabei werden alle Terme des einen Polynoms mit allen Termen des anderen kreuzweise multipliziert und anschließend jene Terme mit gleichen Potenzen von x addiert. Die resultierende Summe bildet das Produktpolynom. Betrachtet man diesen Prozess jedoch aus einer anderen Perspektive, offenbart sich eine elegante Struktur. Anstelle jeden einzelnen Term aufzuschlüsseln und anschließend zusammenzufassen, kann man sich auf die Entstehung eines jeden Koeffizienten des Ergebnispolynoms konzentrieren. Ein praktisches Hilfsmittel dazu ist eine Tabelle, in der die Koeffizienten eines Polynoms horizontal und die des anderen vertikal angeordnet werden.
Die Koeffizienten, die für den gleichen Potenzgrad von x zusammengehören, liegen dabei entlang der sogenannten Diagonalen. Die Summe der Produkte dieser Koeffizienten liefert genau den jeweiligen Ausgabewert. In abstrakter Form lässt sich ein Polynom P durch eine Summe seiner Koeffizienten p_i multipliziert mit den entsprechenden Potenzen x^i darstellen. Wird ein weiteres Polynom R ähnlich dargestellt, ist die Koeffizientenbestimmung des Produkts S für einen gegebenen Index k eine Summation über alle Paare von Koeffizienten, deren Indizes sich zu k addieren. Dies entspricht mathematisch der Formel s_k = Σ p_i * r_{k-i}.
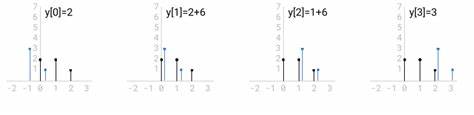
Diese Formel stellt die Grundlage für eine enge Verknüpfung zwischen Polynommultiplikation und Faltung dar. Ein hilfreiches Bild zur Veranschaulichung dieser Methode zeigt das ursprüngliche Polynom P in normaler Reihenfolge und das Polynom R umgekehrt. Dieses Umdrehen geschieht, weil beim Faltungsprozess ein Index von 0 aufwärts zählt, während der andere von seinem Maximalwert hinuntergeht. Durch das Verschieben und Ausrichten der umgekehrten Koeffizienten werden die Produktsummen für jedes x^k leicht nachvollziehbar. Der Zusammenhang zwischen dieser Vorgehensweise und der diskreten Faltung wird deutlich, wenn man die Konzepte von Signalen und Systemen betrachtet.
In der Signalverarbeitung wird ein diskretes Signal als eine Folge von Zahlen verstanden, die zeitlich geordnet sind. Systeme, die auf Signale wirken, können als Funktionen betrachtet werden, die ein Eingabesignal in ein Ausgabesignal transformieren. Ein besonders wichtiger Signaltyp ist der diskrete Impuls, der an einer Stelle den Wert eins und überall sonst null annimmt. Aufgrund seiner Eigenschaften lassen sich beliebige Signale als Kombination versetzter und skalierter Impulse darstellen. Das ermöglicht es, die Wirkung eines Systems auf einen Impuls zu untersuchen – man spricht vom Impulsantwortverhalten.
Für lineare und zeitinvariante Systeme reicht die Kenntnis der Impulsantwort aus, um die Wirkung auf jedes beliebige Signal durch eine Faltung zu bestimmen. Die Faltung zweier diskreter Signale x und h beschreibt mathematisch die Summe aller Produkte von Signalwerten x(k) mit entsprechenden, zeitverschobenen Werten von h(n-k). Dieser Vorgang entspricht exakt der zuvor erläuterten Summation bei der Polynommultiplikation. Dabei erscheint auch hier das unabhängige Durchlaufen eines Indexes k in einer Richtung, während der andere Index n-k in entgegengesetzter Richtung verläuft – was das Umdrehen eines Signals vor der Verschiebung notwendig macht. Anschaulich kann die Faltung als Überlagerung interpretiert werden: Ein Signal wird kontinuierlich an einem anderen Signal entlanggeschoben, wobei zu jedem Zeitpunkt die korrespondierenden Elemente multipliziert und anschließend aufsummiert werden.
Das Faltungsergebnis zeigt somit, wie das eine Signal das andere beeinflusst beziehungsweise filtert. Bemerkenswert ist, dass die Faltung zahlreiche algebraische Eigenschaften besitzt. Sie ist linear, was bedeutet, dass die Faltung von Summen und skalaren Vielfachen von Signalen entsprechend verteilt werden kann. Die Assoziativität garantiert eine flexible Reihenfolge bei der Verarbeitung mehrerer Signale, während die Kommutativität besagt, dass es keine Rolle spielt, welches Signal umgedreht und verschoben wird – die Faltung bleibt gleich. Außerdem gilt die Distributivität, die Faltung und Addition miteinander kombiniert.
Aus praktischer Sicht spielt die Faltung eine zentrale Rolle in der Digitalen Signalverarbeitung. Sie ermöglicht das Filtern von Signalen, das Erkennen von Mustern und viele weitere Anwendungen in Kommunikationssystemen, Bildverarbeitung, Audioanalyse und mehr. Dass Polynommultiplikation und Signalverarbeitung über Faltung tief miteinander verbunden sind, ist kein Zufall. Formal betrachtet bilden Polynome mit üblichen Operationen einen algebraischen Ring, der isomorph zu dem Ring diskreter, endlicher Folgen ist. Diese strukturelle Ähnlichkeit erlaubt es, Verfahren und Erkenntnisse aus einem Bereich auf den anderen zu übertragen.
Weiterhin lassen sich zeitliche Verschiebungen in Signalen durch Multiplikation eines Polynoms mit einem Potenzglied x^k simulieren. Dies erweitert die Einsatzmöglichkeiten von Polynomen in der praktischen Signalbearbeitung. Ein bekannter verwandter Begriff aus der Theorie ist die Verwendung von erzeugenden Funktionen (generating functions), die Folgen als Polynome repräsentieren und so eine algebraisierte Behandlung von Sequenzen ermöglichen. In der Signalverarbeitung wird diese Idee unter anderem im Rahmen der Z-Transformation genutzt, welche diskrete Signale in eine komplexe Frequenzebene überführt und die Analyse linearer Systeme vereinfacht. Daraus resultieren leistungsfähige Techniken zur Systemidentifikation, Filterentwurf und mehr.
Ein weiterer bedeutender Zusammenhang entsteht durch das Faltungstheorem in der Fourier-Transformation. Es beschreibt, dass die Fourier-Transformation einer Faltung zweier Signale dem Produkt ihrer Fourier-Transformationen entspricht. Diese Eigenschaft erlaubt es, Faltungen durch Frequenzmultiplikation und anschließende inverse Transformation sehr effizient zu berechnen, insbesondere unter Einsatz von schnellen Fourier-Transformationsverfahren (FFT). Die Verbindung von Mathematik und Technik in der Betrachtung von Polynompotenzen und Faltungen ist nicht nur theoretisches Fundament; sie erleichtert praktische Algorithmen erheblich. Beispielsweise sind effiziente Verfahren zur Berechnung großer Polynommultiplikationen durch die FFT der Grundstein von zahlreichen Anwendungen in Kryptographie, Computer-Algebra und digitalen Filtern.