Die Durand–Kerner-Methode, auch bekannt als Weierstraß-Verfahren, ist ein bedeutendes numerisches Verfahren zur simultanen Bestimmung aller Nullstellen eines Polynoms. Entwickelt wurde die Methode ursprünglich von Karl Weierstraß im Jahr 1891 und später unabhängig von Durand 1960 sowie Kerner 1966 wiederentdeckt. Trotz ihres Alters hat sie bis heute nichts von ihrer Relevanz eingebüßt und ist insbesondere wegen ihrer Effizienz und Stabilität sehr geschätzt. Vor allem bei der Lösung von Polynomen höherer Ordnung stellt sie eine verlässliche und zugleich einfache Alternative zu komplexeren Algorithmen dar. Die Methode basiert auf einem iterativen Fixpunktverfahren und nutzt komplexe Zahlenarithmetik, um alle Wurzeln gleichzeitig zu approximieren.
Ein großer Vorteil liegt dabei in der gleichzeitigen Berechnung aller Nullstellen, wodurch sich gegenüber iterativen Einzelwortverfahren oftmals ein erheblicher Zeitgewinn bei gleichbleibender Genauigkeit ergibt. Die Anwendung der Durand–Kerner-Methode setzt voraus, dass das zu lösende Polynom normiert ist, das heißt, es besitzt als höchsten Koeffizienten 1. Dieses Vorgehen ist unproblematisch, da Polynomkoeffizienten problemlos durch Division durch den Leitkoeffizienten normiert werden können. Der Ausgangspunkt der Methode ist die Betrachtung des Polynoms in der Form f(x) = (x - P)(x - Q)..
.(x - S), wobei P, Q, R, S die gesuchten Wurzeln sind. Indem man für eine der Wurzeln eine iterative Beziehung herleitet, kann man gegebene Näherungswerte durch immer genauere ersetzt werden. Für eine Wurzel beispielsweise gilt: P = x - f(x)/((x-Q)(x-R)(x-S)). Diese Gleichung suggeriert, dass eine Wurzel als Fixpunktiteration erreicht werden kann, sofern die übrigen Wurzeln bekannt oder approximiert sind.
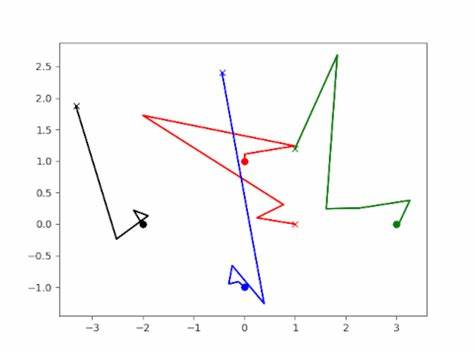
Da diese jedoch unbekannt sind, ersetzt man sie durch aktuelle Näherungswerte und wiederholt das Verfahren gleichzeitig für alle Wurzeln. Die Auswahl der Startwerte ist dabei nicht willkürlich, sondern sollte so erfolgen, dass die Anfangsnäherungen weder zu nahe beieinander liegen noch zu groß sind. Oftmals wird ein Kreis im komplexen Zahlenraum verwendet, der alle Wurzeln mit hoher Wahrscheinlichkeit beinhaltet. Komplexe Startwerte wie 0,4 + 0,9i haben sich als praktisch erwiesen. Bei speziellen Polynomen mit reellen Koeffizienten können Startwerte auch so gewählt werden, dass reale und komplexe konjugierte Wurzeln gezielt herausgefiltert werden.
Die Iterationsvorschrift lautet dann für alle aktuellen Näherungen p, q, r, s: pn = pn-1 - f(pn-1)/((pn-1 - qn-1)(pn-1 - rn-1)(pn-1 - sn-1)) usw. Diese Berechnungen werden so lange iteriert, bis sich die Werte nicht mehr signifikant verändern, was die Konvergenz der Wurzeln signalisiert. Die Methode erfordert daher eine sorgfältige Berechnung und Handhabung von komplexen Zahlen, weshalb sie heutzutage in Softwarepaketen und Programmiersprachen mit umfassender Unterstützung komplexer Arithmetik implementiert ist. Ein weiterer bemerkenswerter Aspekt ist die Konvergenz. Sobald initiale Vermutungen ausreichend nahe an den tatsächlichen Wurzeln liegen, konvergiert die Durand–Kerner-Methode quadratisch.
Das bedeutet, dass der Fehler mit jedem Iterationsschritt ungefähr quadriert wird, was eine sehr schnelle Annäherung impliziert. Allerdings garantiert die Methode keine allgemeine Konvergenz für beliebige Startwerte. Es gibt bekannte Beispiele, bei denen Iterationen in periodische Zyklen abdriften und somit nicht zu einem echten Nullpunkt führen. Trotzdem ist die Durand–Kerner-Methode in der Praxis wegen der typischerweise einfachen Auswahl guter Anfangswerte und ihrer robusten Performance weit verbreitet. Zusätzlich findet die Methode Verwendung in verschiedenen Algorithmen zur numerischen Algebra, etwa zur Faktorisierung von Polynomen oder in Kombinatorik und Algorithmik, wo schnelle und präzise Nullstellenbestimmung gefragt ist.
Ein historisch interessanter Zugang zur Durand–Kerner-Methode ist ihre Herleitung als mehrdimensionale Newton-Methode. Anstatt eine einzelne Gleichung mit einer Variablen zu lösen, betrachtet das Verfahren das Vieta-Theorem und die mit den Wurzeln verknüpften symmetrischen Polynome. So wird ein System von Gleichungen in Bezug auf die Nullstellen formuliert, für das man iterativ Lösungen sucht. Diese Sichtweise bietet tiefe Einsicht in die mathematische Struktur des Verfahrens und verbindet es mit fundamentalen Konzepten der numerischen Mathematik. Die Durchlässigkeit der Theorie spiegelt sich auch im Zusammenhang mit Gerschgorin’schen Kreisen wider.
Diese liefern eine geometrische Interpretation der Iterationen durch eingeschlossene Kreismengen, in denen die Wurzeln liegen. Mit jeder Iteration werden diese Bereiche präziser, was die konvergente Natur der Methode erklärt und angewandt zur Einschätzung und Verbesserung von Anfangswerten dient. Dabei zeigt sich ein spannendes Zusammenspiel zwischen Algebra, numerischer Analysis und geometrischer Anschauung, das den Reiz und die Tiefe der Durand–Kerner-Methode ausmacht. In der Praxis eignet sich das Verfahren hervorragend für Computer Anwendungen, die neben Genauigkeit auch Effizienz benötigen. Die Implementierung erfolgt meist in Hochsprachen wie C++, Python, MATLAB oder dem Open-Source Adapter Julia.
Die Fähigkeit, alle komplexen Wurzeln in einem Rutsch zu bestimmen, lässt sich gut parallelisieren, was in modernen Mehrkernprozessor-Umgebungen erhebliche Vorteile mit sich bringt. Besonders bei polynomiellen Gleichungen mit hohen Graden zahlt sich die Simultanlösung aus, da iterative Methoden, die Wurzeln nacheinander berechnen, oft ineffizient oder fehleranfällig sind. Ein illustratives Beispiel findet sich bei der Lösung eines kubischen Polynoms wie f(x) = x^3 - 3x^2 + 3x - 5 = 0. Die Startwerte bewegen sich zunächst scheinbar chaotisch im komplexen Raum, doch innerhalb weniger Iterationen stabilisieren sich die Annäherungen und liefern hochpräzise Wurzeln inklusive komplexer Konjugierter. Dies verdeutlicht, wie die Methode trotz einfacher Formeln ästhetisch und effizient Wurzeln findet, die sich andernfalls schwer berechnen lassen.
Zusammenfassend bietet die Durand–Kerner-Methode ein höchst praktisches und theoretisch fundiertes Werkzeug zur Bestimmung von Polynomnulstellen. Ihre Kombination aus einfacher Handhabung, simultaner Berechnung und schneller Konvergenz macht sie zu einer festen Größe in der numerischen Mathematik. Mit wachsender Rechenleistung und fortschreitender Integration in numerische Bibliotheken wird sie auch künftig eine bedeutende Rolle beim Lösen algebraischer Gleichungen spielen. Anwender profitieren von einem Verfahren, das zwar mathematische Tiefe besitzt, aber gleichzeitig pragmatisch auf die Bedürfnisse moderner Anwendungen abgestimmt ist.