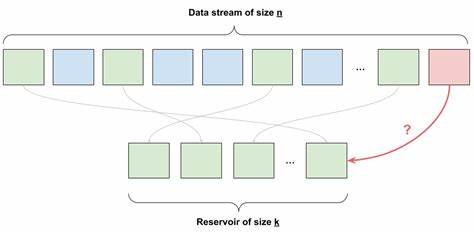
In der heutigen datengetriebenen Welt ist es oft notwendig, aus riesigen oder sogar unbestimmten Datenmengen fair und effizient Stichproben zu ziehen. Ein klassisches Problem entsteht, wenn die Gesamtgröße der Datenquelle nicht bekannt ist oder der Speicherplatz begrenzt bleibt. Hier kommt das sogenannte Reservoir Sampling ins Spiel, eine elegante und effiziente Methode, die eine zufällige Auswahl aus einem dynamischen Datenstrom ermöglicht, ohne die gesamte Datenmenge im Speicher halten zu müssen. Reservoir Sampling ist ein Algorithmus, der sich dadurch auszeichnet, dass er stets eine faire Zufallsauswahl aus den bisher gesehenen Daten garantiert, selbst wenn die Daten kontinuierlich ankommen und ihre Gesamtzahl unbekannt bleibt. Die Herausforderung besteht darin, bei jeder neu ankommenden Datenaufnahme zu entscheiden, ob diese in der Stichprobe aufgenommen wird oder nicht, während gleichzeitig die bisher ausgewählten Elemente eventuell ersetzt werden müssen.
Stellen Sie sich das so vor: Man bekommt Datenstücke eins nach dem anderen präsentiert, ohne zu wissen, wie viele noch folgen werden. Man soll jederzeit eine zufällige Auswahl bleiben, wobei jede Datenaufnahme die gleiche Wahrscheinlichkeit haben muss, Teil der Stichprobe zu sein. Das klingt simpel, ist aber ohne spezielle Strategie eine schwierige Aufgabe. Der naive Ansatz, alle Daten zu speichern und erst am Ende auszuwählen, ist meistens nicht machbar, besonders bei großen oder unendlichen Datenströmen. Ein Beispiel für die Anwendung von Reservoir Sampling findet sich in der Überwachung von Log-Dateien für große IT-Systeme.
In solchen Systemen können die eingehenden Log-Datenmengen in kürzester Zeit immense Ausmaße annehmen, besonders dann, wenn Fehler auftreten oder Ereignisse viral gehen. Um die Speicher- und Verarbeitungsressourcen nicht zu überlasten, möchte man nur eine repräsentative Auswahl der Logs genauer betrachten, ohne dabei wichtige Informationen zu verlieren. Reservoir Sampling löst dieses Problem, indem es sicherstellt, dass die Stichprobe zu jedem Zeitpunkt repräsentativ für alle bisher eingegangenen Daten ist – unabhängig von der Gesamtmenge. Dies geschieht, indem man eine feste Größe für das Reservoir, also die Stichprobe, definiert. Anfangs werden die ersten Daten einfach übernommen.
Mit jedem weiteren Datenelement wird mithilfe einer zufälligen Entscheidung bestimmt, ob es ein bereits ausgewähltes Element ersetzt oder verworfen wird. Diese Entscheidung basiert auf einer Wahrscheinlichkeit, die sich an der Anzahl der bislang verarbeiteten Daten orientiert. Das Prinzip dahinter ist mathematisch beeindruckend einfach. Wenn man zum Beispiel nur ein einzelnes Element auswählen möchte, hat das erste Datenstück eine hundertprozentige Chance, in das Reservoir zu gelangen. Kommt das zweite hinzu, so entscheidet man mit einer Wahrscheinlichkeit von 1 zu 2 darüber, das aktuelle Element zu ersetzen.
Beim dritten ist die Wahrscheinlichkeit 1 zu 3, und so weiter. Diese Methode gewährleistet, dass am Ende jedes Element die gleiche Chance hat, ausgewählt zu sein, unabhängig davon, wann es eingetroffen ist. Wichtig ist, dass Reservoir Sampling nicht nur auf eine einzelne Auswahl beschränkt ist. Wenn mehrere Elemente gleichzeitig ausgewählt werden sollen, erweitert sich das Prinzip entsprechend. Dabei besitzt jedes neue Element eine k zu n Chance, in das Reservoir aufgenommen zu werden, wobei k die Größe der Stichprobe und n die Anzahl der bisher eingegangenen Elemente ist.
Falls ein neues Element ausgewählt wird, wird eines der bestehenden Reservoir-Elemente nach dem Zufallsprinzip ersetzt. Dieses Verfahren behält die Gleichverteilung und Fairness bei und sorgt dafür, dass sich trotz Limitierung der Speicherkapazität eine authentische, zufällige Stichprobe bildet. Die Anwendungsmöglichkeiten von Reservoir Sampling sind vielfältig. Neben der erwähnten Log-Datenanalyse eignet sich der Algorithmus auch für Streaming-Daten in Sozialen Medien, bei der Analyse von Netzwerkdaten oder bei der Verarbeitung großer wissenschaftlicher Experimente, deren Datenvolumen regulär zu hoch ist, um vollständig gespeichert zu werden. Da der Algorithmus nur konstante bzw.
vorab festgelegte Speicherressourcen benötigt, ist er besonders für ressourcenbeschränkte Umgebungen oder Echtzeitanwendungen geeignet. Ein weiterer Vorteil von Reservoir Sampling ist seine Einfachheit in der Implementierung, die keine komplexen mathematischen Operationen voraussetzt. Die Kernausführung benötigt lediglich einfache Zufallszahlengeneratoren und elementare Berechnungen. Diese Eigenschaft macht ihn sehr attraktiv für den Einsatz in unterschiedlichsten Softwarelösungen – von Microservices bis hin zu eingebetteten Systemen. Doch Reservoir Sampling bringt auch einige Herausforderungen mit sich.
Da mit zunehmender Anzahl von eingegangenen Daten nur noch eine kleine Chance besteht, neue Elemente in das Reservoir aufzunehmen, ist die Stichprobe in frühen Phasen stark von den ersten Daten beeinflusst und kann somit unter Umständen weniger repräsentativ sein, wenn die Datenverteilung im Zeitverlauf variiert. Um solche Effekte zu minimieren, kann man Zeitfenster definieren, in denen neue Reservoirs aufgebaut werden, und die bisherigen Stichproben periodisch zurücksetzen. Darüber hinaus existieren gewichtete Varianten des Reservoir Sampling, bei denen einzelne Elemente eine höhere oder geringere Chance haben, in die Stichprobe zu gelangen, je nachdem, wie wertvoll oder relevant sie sind. Solche gewichteten Algorithmen sind besonders hilfreich, wenn bestimmte Datenkategorien besonders berücksichtigt werden sollen, zum Beispiel Fehlerlog-Einträge, die immer behalten werden sollen, unabhängig von ihrer Häufigkeit. Trotz der bestehenden Limitationen ist Reservoir Sampling eine der elegantesten und effizientesten Methoden zur Behandlung von Stichproben aus unbekannter oder unbegrenzter Datenmenge.
Es ermöglicht Unternehmen und Entwicklern, wichtige Entscheidungen auf Basis fairer, zufälliger und dennoch ressourcenschonender Stichproben zu treffen. In der Praxis unterstützen viele Programmiersprachen und Softwarebibliotheken heute bereits Implementierungen dieses Algorithmus, wodurch der Einstieg und die Integration in bestehende Systeme erleichtert werden. Dabei ist es ratsam, neben der korrekten Implementierung auch eine sorgfältige Überwachung der Datenströme zu etablieren, um zu überprüfen, ob die durch das Reservoir Sampling generierten Stichproben auch den gewünschten Zweck erfüllen. Reservoir Sampling bietet eine Lösung für das klassische Dilemma, dass Speicher und Verarbeitungszeit begrenzt sind, die Datenmenge aber unbegrenzt oder zumindest nicht im Voraus bekannt ist. Die Fähigkeit, im Vorbeigehen und mit konstanter Speichergröße eine faire Stichprobe aus einem potenziell unendlichen Strom zu ziehen, macht diesen Algorithmus zu einem wertvollen Werkzeug in der modernen Datenanalyse.
Zusammengefasst ist Reservoir Sampling nicht nur ein theoretisch schöner Algorithmus, sondern ein praktisches Hilfsmittel für die Datenverarbeitung, das sich in zahlreichen Anwendungsszenarien bewährt hat. Die Balance zwischen Einfachheit, Effizienz und Fairness in der Stichprobenauswahl macht Reservoir Sampling zu einem unverzichtbaren Bestandteil moderner datengetriebener Systeme.