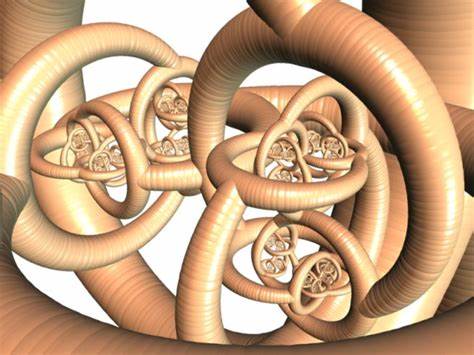
Die Alexander-Hornkugel ist ein hochinteressantes und zugleich komplexes Objekt aus dem Bereich der Topologie, das 1924 von J.W. Alexander entdeckt wurde. Es handelt sich dabei um eine spezielle Einbettung einer zweidimensionalen Kugel in den dreidimensionalen euklidischen Raum. Im Gegensatz zu einer gewöhnlichen Kugel, wie wir sie uns im Alltag vorstellen, weist die Alexander-Hornkugel eine außergewöhnlich verwickelte Struktur auf, die sie zu einem der klassischen Beispiele für sogenannte „wilde“ Embeddings macht.
Diese wilden Einbettungen zeigen, wie drastisch sich das allgemeine Verständnis von Raum und Form erweitern lässt, wenn man die streng mathematischen, topologischen Aspekte einer Oberfläche oder eines Körpers untersucht. Die Konstruktion selbst ist faszinierend und beruht auf einem iterativen Prozess, der immer wieder neue Verzweigungen und „Hörner“ hinzufügt, was der Figur ihren Namen verleiht. Ausgehend von einem Standardtorus wird an einer Stelle ein radialer Ausschnitt entfernt. An den Schnittkanten werden dann zwei weitere, jeweils mit Löchern versehene Tori befestigt, die sich gegenseitig verschlingen. Dieser Vorgang wiederholt sich fortlaufend unendlich oft, wodurch eine immer komplexere Struktur entsteht.
Was auf den ersten Blick wie ein chaotisches Gebilde aussieht, ist streng mathematisch wohl definiert und besitzt interessante Eigenschaften. So ist die sogenannte „innere“ Alexander-Hornkugel topologisch gesehen ein 3-Ball und somit einfach zusammenhängend. Das bedeutet, dass jede geschlossene Schleife innerhalb dieses Raumes zu einem Punkt zusammengezogen werden kann, ohne den Raum zu verlassen. Besonders bemerkenswert ist jedoch, dass das Komplement der Hornkugel im dreidimensionalen Raum nicht einfach zusammenhängend ist. Eine Schleife, die den komplex verschlungenen Teil der Struktur umgibt, lässt sich nicht ohne Kontakt mit der Hornkugel zu einem Punkt zusammenziehen.
Diese Eigenschaft hebt die Alexander-Hornkugel deutlich von der gewohnten Kugel ab, deren Außenseite stets einfach zusammenhängend ist. Die Entdeckung dieses Phänomens hatte weitreichende Konsequenzen für die Topologie. Insbesondere zeigte sie, dass der Jordan-Schönflies-Satz, der im zweidimensionalen Raum gilt und besagt, dass eine einfache geschlossene Kurve die Ebene in zwei zusammenhängende Bereiche teilt, in der Form nicht auf drei Dimensionen verallgemeinert werden kann. Das bedeutet, dass das intuitive Verständnis, eine Kugel trenne den Raum in zwei einfache Regionen, hier versagt. Die Alexander-Hornkugel bringt vielmehr eine komplexe Trennung hervor, die das Verständnis räumlicher Einbettungen erheblich erweitert hat.
Ein weiterer wichtiger Aspekt ist die Unterscheidung der Kategorien von Mannigfaltigkeiten, die durch die Alexander-Hornkugel besonders deutlich wird. Alexander bewies, dass der Jordan-Schönflies-Satz in drei Dimensionen für glatt oder stückweise linear eingebettete Kugeln gültig ist, jedoch nicht für allgemein topologische Einbettungen wie die Hornkugel. Dies legt nahe, dass topologische, differenzierbare und stückweise lineare Mannigfaltigkeiten strikt voneinander unterschieden werden müssen. Auch zukünftig hat die Alexander-Hornkugel Einfluss auf theoretische Forschungen gehabt. Der sogenannte „solide“ Alexander-Hornkugel, also die geschlossene nicht einfach zusammenhängende Komplementärregion, ist kein Mannigfaltigkeitsraum im klassischen Sinne.
Interessanterweise zeigte R.H. Bing, dass das doppelte Ankleben zweier solcher soliden Hornkugeln aneinander eine 3-Sphäre ergibt, also topologisch äquivalent zum dreidimensionalen Einheitskugelraum ist. Diese Erkenntnis illustriert, wie selbst komplexe, „wild“ eingebettete Strukturen durch geschickte topologische Operationen einfache globale Formen zurückgeben können. Die Alexander-Hornkugel ist auch ein Beispiel für sogenannte „zerknitterte Würfel“ (crumpled cubes), die als abgeschlossene Bereiche in der 3-Sphäre entstehen, wenn man einen eingebetteten 2-Sphärenraum vom Rest der 3-Sphäre trennt.
Neben der klassischen Hornkugel lassen sich durch Variationen des Konstruktionsverfahrens auch andere „gehörnte“ Kugeln erzeugen, beispielsweise indem man mehr Hörner in jedem Iterationsschritt hinzufügt oder analog in höheren Dimensionen arbeitet. Diese Verallgemeinerungen erweitern das Bild der vielfältigen und oft kontraintuitiven Formen, die in der Topologie existieren. Es gibt auch alternative Konstruktionen von wilden Einbettungen, ein bekanntes Beispiel ist die Antoine-Hornkugel, die auf einer ähnlichen Idee basiert und eine komplizierte Einbettung des Cantor-Sets in die 3-Sphäre darstellt. Solche „wilden“ topologischen Objekte spielen eine wichtige Rolle beim Verständnis der Struktur von 3-Mannigfaltigkeiten und den Grenzen klassischer topologischer Sätze. Die Bedeutung der Alexander-Hornkugel für die Mathematik ist also nicht nur historisch durch ihre Entdeckung gegeben, sondern auch in ihrer anhaltenden Rolle als Beispiel für die Tiefe und Komplexität topologischer Strukturen.
Sie zeigt eindrücklich, wie das Studium abstrakter mathematischer Konzepte zu überraschenden Ergebnissen führen kann, die weit über die intuitive Geometrie hinausgehen. Für Forscher und Mathematikinteressierte bleibt die Alexander-Hornkugel ein faszinierendes Gegenstand der Untersuchung, der sowohl die Schönheit als auch die Herausforderungen der geometrischen Topologie repräsentiert. Das Verständnis solcher komplexer topologischer Figuren legt zudem Grundlagen für weiterführende Theorien, etwa in der Knotentheorie oder bei der Untersuchung höherdimensionaler Mannigfaltigkeiten, die ihre Anwendungen in verschiedenen Bereichen der Mathematik und der theoretischen Physik finden. Insgesamt verkörpert die Alexander-Hornkugel ein Paradebeispiel mathematischer Kreativität und Eleganz, das zugleich den Weg für zahlreiche weitere Forschungen eröffnet hat und nach wie vor eine Quelle von Inspiration und Erkenntnis ist.