Constraint Logic Programming over Finite Domains, kurz CLPFD, ist eine leistungsfähige Erweiterung von Prolog, die insbesondere bei der Lösung komplexer kombinatorischer Probleme eine wesentliche Rolle spielt. Die Implementierung von CLPFD im N-Prolog-System stellt nicht nur eine technische Herausforderung dar, sondern ist auch eine Reise, bei der grundlegende Paradigmen im Denken über Programmierung und Problemlösung neu bewertet werden müssen. Im Folgenden wird auf die verschiedenen Aspekte eingegangen, die das Arbeiten mit CLPFD so faszinierend machen und wie diese Technologie in N-Prolog umgesetzt wird. Die traditionelle Prolog-Programmierung beruht hauptsächlich auf rückwärtsgerichteter Schlussfolgerung: Das System versucht, von einem Ziel ausgehend Schritt für Schritt passende Fakten oder Regeln zu finden, die zu einer Lösung führen. CLPFD hingegen benötigt ein vorwärts gerichtetes Denken, das gewisse mentale Anpassungen erfordert, aber gleichzeitig erhebliche Vorteile birgt.
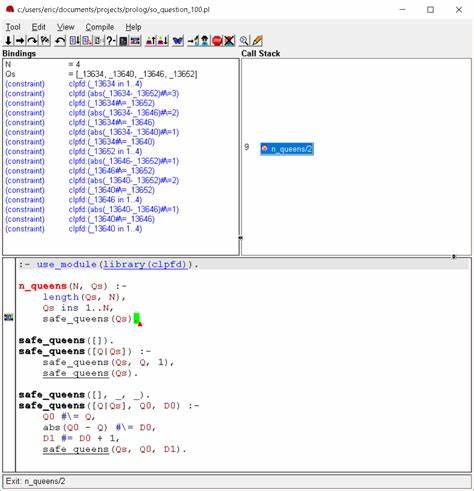
Das Hauptprinzip von CLPFD ist, dass Variablen nicht einfach mit beliebigen Werten belegt werden, sondern mit Integer-Domänen, also Wertebereichen, die auf diskrete Zahlen beschränkt sind. Durch das Anwenden von Beschränkungen (Constraints) können diese Wertebereiche eingeschränkt und dadurch die Menge gültiger Lösungen effizient eingegrenzt werden. Diese prädiktive Einschränkung reduziert die Suchräume drastisch und macht Probleme, die traditionell als komplex galten, deutlich lösbarer und schneller. Das berühmte N-Damen-Problem, das darin besteht, N Damen so auf einem Schachbrett zu platzieren, dass keine zwei Damen sich gegenseitig schlagen, dient als klassisches Beispiel. Während traditionelle Algorithmen oft auf Generierung und anschließender Prüfung von Permutationen beruhen und dabei aufwendig alle ungültigen Zustände aussortieren, macht CLPFD diesen Prozess eleganter und effizienter.
Statt mühsam alle Fälle prüfen zu müssen, werden mit CLPFD die Einschränkungen direkt ins System eingebaut, sodass ungültige Zuweisungen von Anfang an ausgeschlossen werden. Diese automatische und intelligente Beschneidung des Suchraums kennzeichnet die Stärke dieser Technologie. Die Umsetzung von CLPFD-Komponenten im N-Prolog-System erforderte einen tiefen Einblick in die interne Repräsentation von Variablen und deren Wertebereichen. Ein besonderes Augenmerk lag auf der effizienten Speicherung und Verarbeitung der Domains, was letztlich im N-Prolog zum Entwurf von speziellen C-Komponenten für die Domänenerzeugung führte. Durch den Einsatz von Arrays zur repräsentativen Speicherung der Integer-Domänen und die Index-basierte Verwaltung konnte eine hohe Performance gewährleistet werden.
Diese Arrays werden bei Bedarf in Prolog-kompatible Datenstrukturen umgewandelt, insbesondere während der Phase des Labelings, bei der konkrete Lösungen für die Variablen gefunden werden. Ein zentraler Bestandteil von CLPFD in Prolog ist das Prädikat all_different/1. Dieses gewährleistet, dass alle Variablen in einer Liste unterschiedliche Werte annehmen. Für die erfolgreiche Umsetzung des N-Damen-Problems ist die korrekte Implementierung dieser Funktionalität essenziell. In N-Prolog wurde all_different/1 so realisiert, dass es die Variablen effizient überwacht und entsprechend mit ihren zulässigen Domains verknüpft, sodass es während des Lösungsprozesses fortwährend aktiv bleibt.
Ein wichtiger technischer Schritt bestand darin, Variablen mit Tags zu versehen, die deren Eigenschaft zur Einzigartigkeit überwachen. Diese Markierung erleichtert die Rückverfolgung und Anpassung der Domains im Verlauf der Constraint-Auswertung. Die Herausforderung bei CLPFD liegt auch darin, komplexe Constraints in eine für die Maschine verständliche und effiziente Form zu bringen. Besonders bei arithmetischen Ausdrücken mit Variablen wie X + Y + Z #= 3 zeigt sich, wie wichtig es ist, diese Ausdrücke zu normalisieren. In N-Prolog wurde die Methode verfolgt, die Variablen auf der linken Seite zu sammeln und Konstanten auf die rechte Seite zu übertragen.
Dadurch lassen sich Werte schrittweise zuweisen und während der Suche überprüft werden, ob die verbleibenden Variablen unter ihren jeweiligen Domäneneinschränkungen weiterhin gültige Werte annehmen können. Das manuelle Nachverfolgen und Umformen solcher Constraints war zunächst eine intellektuelle Herausforderung für die Entwickler. Sie wurde zum Beispiel mit Stift und Papier nachvollzogen, um die theoretischen Abläufe genau zu verstehen und daraus effizientere Computermodelle zu entwickeln. Diese Herangehensweise sicherte eine präzise und nachvollziehbare Implementierung. CLPFD hebt sich durch seine Fähigkeit hervor, in der Lösungsfindung automatische Domänenreduktionen durchzuführen, die sehr effektiv zum schnellen Ausschluss ungültiger Lösungen beitragen.
Im Vergleich zu herkömmlichen Methoden spart dies nicht nur Rechenzeit, sondern macht auch das Programmierparadigma intuitiver, weil man sich mehr auf die formalen Beschränkungen und weniger auf explizite Suchstrategien konzentriert. Die Integration von CLPFD im N-Prolog kann als ein bedeutender Fortschritt angesehen werden, da diese Ergänzung das native Prolog-System mit einer modernen und effizienten Form der Constraint-Verarbeitung erweitert. Dies eröffnet nicht nur neue Möglichkeiten bei der Problemanalyse und -lösung, sondern stellt auch die Weichen für eine verbesserte Nutzererfahrung im Umgang mit logikbasierten Systemen. Ein zukünftig wichtiger Schritt wird die Verfeinerung der Suchstrategien für die Auswahl von Wertzuweisungen sein, um noch gezielter und schneller Lösungen aus den dominierten Variablen zu extrahieren. Optimierungen im Bereich der Heuristiken während des Labeling-Prozesses versprechen dabei eine weitere Verbesserung der Performance.