Die Ursprung der impliziten Regularisierung im Stochastischen Gradientenabstieg verstehen

Die Entwicklung von tiefen neuronalen Netzwerken hat die Welt des maschinellen Lernens revolutioniert. Eines der zentralen Rätsel, das Wissenschaftler und Praktiker seit Jahren beschäftigt, ist die bemerkenswerte Fähigkeit dieser Netzwerke, nicht nur Trainingsdaten nahezu perfekt zu interpolieren, sondern gleichzeitig starke Generalisierungsleistungen auf ungesehenen Daten zu erzielen. Während traditionelle Lerntheorien den Fokus auf die Modellklassen und Verlustfunktionen legten, zeichnet sich immer deutlicher ab, dass vor allem die verwendeten Optimierungsalgorithmen eine entscheidende Rolle für das Gelingen spielen. Besonders der Stochastische Gradientenabstieg (SGD) hebt sich hierbei als Schlüsselfaktor heraus. Sein Einfluss auf die Präferenz bestimmter Minima der Loss-Landschaft, und die daraus resultierende sogenannte implizite Regularisierung, ist ein spannendes und aktuelles Forschungsthema.

Das zentrale Problem, das Wissenschaftler versuchen zu verstehen, ist nicht nur, wie SGD das Optimierungsproblem bewältigt, sondern vielmehr, warum es genau die Minima auswählt, die zu guten Generalisierungsergebnissen führen. Im Gegensatz zu klassischen Theorien, die davon ausgehen, dass jedes gut trainierte Modell auf einem Minimum der Verlustfunktion gleichwertig gut ist, zeigt die Praxis, dass viele solcher Minima existieren, die sich im Trainingsfehler kaum unterscheiden. Ihre Fähigkeit, auf unbekannten Daten korrekt zu generalisieren, variiert jedoch stark. Die implizite Regularisierung von SGD beschreibt das Phänomen, dass der Optimierungsprozess selbst dazu tendiert, auf bestimmte Lösungen zu konvergieren, die bessere Generalisierungsfähigkeit besitzen. Eine Schlüsselidee zur Analyse von SGD stammt aus der Idee, Optimierungsschritte als diskretisierte Versionen eines kontinuierlichen Prozesses darzustellen, nämlich des Gradientenflusses, beschrieben durch Differentialgleichungen.

Die herkömmliche Betrachtung, die Neural Tangent Kernel Theorie, modelliert das Training bei sehr kleinen Lernraten und Vollbatch-Gradienten als stetigen Fluss. Diese Perspektive kann wertvolle Einsichten bieten, ist aber in der Praxis oft nicht ausreichend, da reale Trainingsprozesse mit endlichen Lernraten und insbesondere mit stochastischen, mini-batch-basierten Gradientenupdates ablaufen. Im Mittelpunkt der jüngsten Forschungen steht daher die Untersuchung, wie genau das diskrete und stochastische Verhalten von SGD sein Verhalten beeinflusst. Die Methode der sogenannten Rückwärtsfehleranalyse (backward error analysis) bietet hier ein mächtiges Werkzeug. Dabei wird versucht, eine modifizierte Differentialgleichung zu finden, deren Lösung einer kontinuierlichen Trajektorie nahekommt, die das diskrete Optimierungsverhalten realistisch abbildet.

Auf diese Weise kann man verstehen, welche zusätzlichen Dynamiken durch die endliche Schrittweite und die Stochastizität durch Mini-Batches entstehen. Eine bemerkenswerte Erkenntnis ist, dass Gradient Descent mit einer endlichen Schrittweite effektiv einem Gradient Flow mit einem ergänzenden Regularisierungsterm auf die Gradienten entspricht. Dieser Zusatz term, bekannt als implizite Gradientenregularisierung, wirkt wie eine Strafe für große Gradienten und predisponiert das System, flachere und robustere Minima zu bevorzugen. Barrett und Dherin zeigten in einer zeitgleich erschienenen Arbeit, dass genau dieses Modell den Effekt des „Implicit Gradient Regularization“ beschreibt und somit einen expliziten analytischen Ausdruck für diesen subtilen Mechanismus liefert. Bei SGD ist die Situation komplexer, da die Pfade aufgrund der zufälligen Auswahl der Mini-Batches eine ganze Verteilung von möglichen Trajektorien bilden.

Das Optimierungsverhalten lässt sich so nicht durch eine einzige Trajektorie beschreiben, sondern eher durch eine Verteilung möglicher Endpunkte. Smith und Kollegen erweiterten nun diese Analyse auf SGD mit kleineren, aber nicht infinitesimal kleinen Lernraten und zeigten, dass SGD einem modifizierten Optimierungsprozess auf eine andere Loss-Funktion folgt. Diese modifizierte Verlustfunktion beinhaltet neben dem Originalverlust einen zusätzlichen Regularisierungsterm, der sich aus der Varianz der Mini-Batch-Gradienten zusammensetzt. Diese Varianzterm—man kann ihn als die durchschnittliche Streuung der Gradienten über alle Mini-Batches verstehen—verhindert, dass der Optimierungsprozess in Regionen der Parameterlandschaft hängen bleibt, in denen die Mini-Batch-Verluste stark divergieren. Dies führt dazu, dass SGD nicht nur andere Trajektorien als das klassische Gradient Descent verfolgt, sondern grundsätzlich auch auf andere Minima konvergiert.

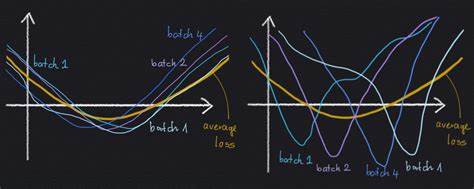
Diese Minima sind charakterisiert durch eine geringe Varianz der Gradienten über Mini-Batches, was mit einer robusteren und weniger empfindlichen Lösung einhergeht. Ein anschauliches Bild dafür sind zwei Minima, die beide gleich tief sind und ähnliche Breiten besitzen, sich aber in ihrer Stabilität gegenüber Mini-Batch-Variationen unterscheiden. Ein Minimum, das aus ähnlichen und weit offenen Mini-Batch-Verlusten entsteht, wird bevorzugt, da es auf unterschiedliche Datenstichproben konsistent stabile Ergebnisse liefert. Im Gegensatz dazu ist ein Minimum mit großen Mini-Batch-Unterschieden wesentlich sensibler für die Datenaufteilung und kann schlechtere Generalisierungsleistungen zeigen. Hier zeigt sich ein möglicher Ursprung der Überlegenheitsleistung von SGD: Das Optimierungsverfahren implizit regularisiert die Lösung, indem es eine minimale Varianz der Mini-Batch-Gradienten erzwingt und damit zu robusteren Modellen führt.

Darüber hinaus hat die Analyse auch Implikationen für das Design von Optimierungsalgorithmen beziehungsweise für das Verständnis verschiedener Varianten von SGD. Zum Beispiel hängt der genaue Regularisierungseffekt davon ab, wie genau die Mini-Batches gebildet werden und wie die Randomisierung der Daten erfolgt. Die etablierte Analyse nimmt an, dass die Daten zunächst fest den Mini-Batches zugeordnet werden und nur die Reihenfolge der Mini-Batches zufällig variiert wird, im Gegensatz zu einem Sampling mit Zurücklegen einzelner Datenpunkte. Es ist denkbar, dass sich der Effekt mit anderer Samplingstrategie verändert. Dies unterstreicht die Bedeutung der feinen technischen Details für die Dynamik des Optimierungsprozesses.

Die Arbeit von Smith, Dherin und Kollegen liefert somit eine bedeutende Erweiterung der theoretischen Grundlagen, die uns hilft zu verstehen, warum SGD so effektiv ist. Die Erkenntnisse zur impliziten Regularisierung bieten einen tiefen Einblick in den Lernprozess, die weit über klassische Erklärungen auf Basis von Modellklasse und Verlustfunktion hinausgehen. Sie zeigen, dass der Trainingsalgorithmus selbst eine Art von Regularisierung implementiert, ohne dass explizite Regularisierer eingeführt wurden. Diese implizite Regularisierung erklärt auch, warum eine zu kleine Lernrate nicht notwendigerweise zu besseren Ergebnissen führt. Denn gerade die endliche Schritteweite erzeugt diesen Regularisierungseffekt durch die zusätzlichen Terme in der modifizierten Differentialgleichung.

Zu kleine Lernraten können diesen Effekt abschwächen, was die praktischen Beobachtungen aus der Trainingspraxis bestätigt, in denen moderate Lernraten oft bessere Generalisierungsergebnisse hervorbringen. Der Nutzen dieses Forschungsansatzes liegt nicht nur in der rein theoretischen Erklärung, sondern hat auch praktische Auswirkungen auf das Verständnis und die Optimierung von Trainingsprozessen. Forscher und Entwickler können durch gezieltes Einstellen von Lernraten, der Mini-Batch Größe und der Samplingstrategie Einfluss darauf nehmen, wie stark die implizite Regularisierung wirkt und somit die Generalisierungsleistung ihrer Modelle verbessern. Auch wenn die Theorie einiges klärt, bleibt die Optimierung in hochdimensionalen, nicht-konvexen Landschaften von neuronalen Netzen weiterhin komplex und teilweise rätselhaft. Die vorgestellte Arbeit leistet einen wertvollen Beitrag zum besseren Verständnis der verborgenen Mechanismen, die den Erfolg von SGD ermöglichen.

Zugleich fordert sie dazu auf, hinsichtlich der Auswirkungen von Optimierungsparametern und Datenverarbeitung genauer hinzuschauen und experimentell zu erkunden, wie sich diese theoretischen Befunde in der Praxis manifestieren. Zusammenfassend lässt sich sagen, dass die implizite Regularisierung durch den Stochastischen Gradientenabstieg eine fundamentale Rolle in der Fähigkeit moderner neuronaler Netzwerke spielt, robust zu generalisieren. Die Kombination aus stochastischer Mini-Batch-Auswahl und endlichen Schrittweiten führt zu einer konservativen Reise durch den Parameterraum, die sensible Regionen mit hoher Mini-Batch-Gradienten-Varianz meidet. Dieses tieferes Verständnis bietet vielversprechende Perspektiven für weitere Forschung, neue Algorithmen und verbesserte Lernstrategien, die das volle Potenzial neuronaler Netzwerke noch besser ausschöpfen können.