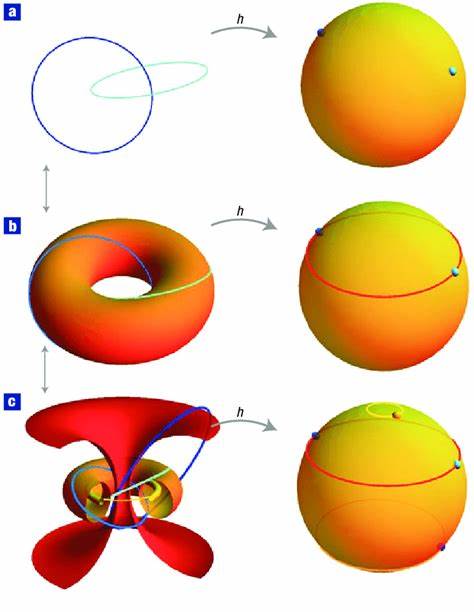
Die Mathematik ist ein weitreichendes Feld, in dem verschiedene Theorien und Konzepte immer wieder miteinander verknüpft und neu interpretiert werden. Zwei solcher bedeutenden Themen sind elliptische Kurven und die Hopf-Fibration. Beide erscheinen auf den ersten Blick in sehr unterschiedlichen Kontexten, doch ihre Verbindung eröffnet spannende Perspektiven für ein besseres Verständnis abstrakter mathematischer Strukturen und deren Visualisierung. Elliptische Kurven sind algebraische Kurven, definiert durch Gleichungen dritten Grades, die schon seit Jahrhunderten in der Zahlentheorie, Kryptographie und algebraischen Geometrie eine zentrale Rolle spielen. Sie zeichnen sich durch ihre besondere Struktur aus, die eine Gruppe auf den Kurvenpunkten erlaubt, was sie zu einem kraftvollen Werkzeug in verschiedenen Disziplinen macht.
Gleichzeitig eröffnet die geometrische Interpretation elliptischer Kurven, insbesondere über komplexen Zahlen, faszinierende Einsichten in topologische und analytische Eigenschaften. Die Hopf-Fibration dagegen stammt aus der Topologie und beschreibt eine außergewöhnliche Struktur, bei der die Dreidimensionale Einheitskugel in Kreise zerlegt wird, die alle auf die Zweidimensionale Sphäre abgebildet werden. Diese Konstruktion gehört zu den schönsten Ergebnissen der Algebraischen Topologie und verdeutlicht, wie komplexe Zusammenhänge durch einfache geometrische Objekte repräsentiert werden können. Die Hopf-Fibration hat darüber hinaus wichtige Anwendungen in der theoretischen Physik, etwa in der Quantenmechanik und der Stringtheorie. Die Verbindung zwischen elliptischen Kurven und der Hopf-Fibration liegt in der Möglichkeit, elliptische Kurven als komplexe Tori zu interpretieren, also als Produkt von zwei Kreisen, die durch eine komplexe Struktur miteinander verschränkt sind.
Diese Interpretation knüpft direkt an die Eigenschaften der Hopf-Fibration an, da beide Strukturen auf Kreisen basieren und somit topologisch und geometrisch miteinander verwoben sind. Durch diese Verbindung können Mathematiker ein tiefgehenderes Verständnis über die Form, Symmetrie und Dynamik elliptischer Kurven gewinnen. In der modernen Mathematik wird viel Wert auf die Visualisierung abstrakter Konzepte gelegt, besonders wenn diese mehrere Dimensionen oder komplexe Strukturen beinhalten. Hier spielen moderne 3D-Darstellungen eine besondere Rolle, indem sie es ermöglichen, elliptische Kurven und die Hopf-Fibration anschaulich und verständlich zu machen. So können beispielsweise elliptische Kurven, die klassisch durch Gleichungen charakterisiert sind, als reale Flächen oder Tori im dreidimensionalen Raum dargestellt werden.
Diese Visualisierungen helfen nicht nur Forschern, sondern auch Studierenden, intuitivere Zugänge zu finden und die tiefere Bedeutung dieser mathematischen Objekte besser zu erfassen. Die Erforschung elliptischer Kurven ist aber nicht nur für theoretische Zwecke bedeutsam, sondern hat auch praktische Anwendungen. Insbesondere in der Kryptographie sind elliptische Kurven von größter Bedeutung, da sie sichere und effiziente Verfahren zur Verschlüsselung und digitalen Signatur ermöglichen. Die Verbindung zur Hopf-Fibration kann in diesem Kontext zur Entwicklung neuer Verschlüsselungsmethoden beitragen, indem sie die geometrischen Eigenschaften der Kurven für algorithmische Zwecke zugänglich macht. Ein weiterer spannender Bereich, in dem elliptische Kurven und die Hopf-Fibration zusammenfließen, ist die Stringtheorie.
Dort modellieren Physiker grundlegende Partikel und ihre Wechselwirkungen mit Hilfe von topologischen und geometrischen Objekten – genau die Art von Strukturen, die elliptische Kurven und die Hopf-Fibration beschreiben. Durch das Verständnis dieser Konzepte können tiefere Einblicke in die Struktur des Universums gewonnen werden. Historisch gesehen haben elliptische Kurven eine lange Tradition. Bereits in der Antike wurden spezielle Gleichungen untersucht, doch erst mit der Entwicklung moderner Algebra und Topologie wurden ihre komplexen Strukturen und Zusammenhänge vollständig erkannt. Die Hopf-Fibration wurde erst im 20.
Jahrhundert entdeckt und hat seitdem durch ihre Eleganz und einzigartigen Eigenschaften starken Einfluss auf viele mathematische Forschungsgebiete gewonnen. Die Kombination beider Konzepte in wissenschaftlichen Arbeiten, wie in der aktuellen Forschung, zeigt den Trend, interdisziplinär zu denken und Werkzeuge aus verschiedenen Bereichen zu vereinen. Das Zusammenspiel von algebraischer Struktur, topologischer Faserung und geometrischer Visualisierung ist beispielhaft für diese Herangehensweise und eröffnet zahlreiche neue Forschungsansätze. Interessanterweise lässt sich die Hopf-Fibration nicht nur mathematisch abstrakt beschreiben, sondern auch experimentell oder digital eindrucksvoll darstellen. Moderne Computergrafik und interaktive Software erlauben es, komplexe Faserungen zu visualisieren, die für das menschliche Auge sonst unsichtbar sind.
Dies fördert das allgemeine Verständnis und bietet neue Möglichkeiten, mathematische Phänomene zu lehren. Elliptische Kurven und die Hopf-Fibration sind somit nicht nur Gegenstand akademischer Studien, sondern auch Brücken, die unterschiedliche Bereiche der Mathematik und Physik verbinden. Von der Anzahl der rationalen Punkte auf elliptischen Kurven über die gruppentheoretischen Aspekte bis hin zu tiefgründigen topologischen Einsichten ermöglicht die Beschäftigung mit diesen Themen eine umfassende und vernetzte Perspektive. Für jeden, der sich tiefer mit moderner Mathematik beschäftigen möchte, bietet die Erforschung dieser Zusammenhänge eine spannende Herausforderung. Es gilt, sowohl die abstrakten algebraischen Eigenschaften zu verstehen als auch die geometrischen und topologischen Ansichten zu schätzen.
Dabei zeigt die Verbindung von elliptischen Kurven und der Hopf-Fibration eindrucksvoll, wie vielseitig und reichhaltig mathematische Strukturen sein können. Abschließend lässt sich sagen, dass die Verknüpfung elliptischer Kurven mit der Hopf-Fibration ein Paradigma für modernen interdisziplinären Forschungsgeist darstellt. Es ist ein hervorragendes Beispiel dafür, wie mathematische Konzepte verwoben und in neue Zusammenhänge gestellt werden können, um sowohl theoretische Erkenntnisse als auch praktische Anwendungen voranzutreiben. Die fortschreitende Entwicklung in der Visualisierung dieser Strukturen eröffnet zudem neue Wege, komplexe Ideen einem breiteren Publikum zugänglich zu machen und die Faszination der Mathematik lebendig zu halten.