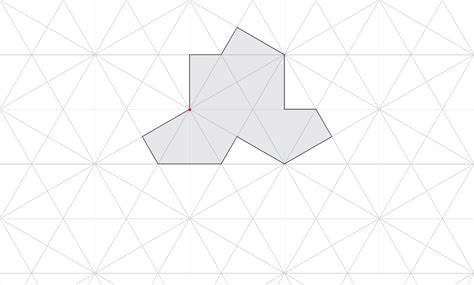
Die Mathematik hält immer wieder Überraschungen bereit, die nicht nur Experten faszinieren, sondern auch für die breite Öffentlichkeit zugänglich werden. Eine dieser jüngsten Entdeckungen betrifft aperiodische Kacheln, speziell die sogenannten Monotiles, die dazu in der Lage sind, eine Ebene unendlich und dabei nichtperiodisch zu überdecken. Ein herausragendes Beispiel hierfür ist der „Hat“, eine Form, die 2022 von David Smith, einem pensionierten Drucktechniker und Amateurmathematiker, entdeckt wurde. Diese Form hat großes Aufsehen erregt, da sie erstmals eine aperiodische Kachel mit nur einem einzigen Tile demonstriert - ein Problem, das in der Mathematik lange Zeit als „Einsteinproblem“ bekannt war. Der „Hat“ besticht dadurch, dass er aus acht sogenannten „Kites“ zusammengesetzt ist, die ihrerseits spezielle, unregelmäßige Formen besitzen.
Seine Fähigkeit, die Ebene ohne wiederkehrende Muster zu füllen, wurde auch durch viele renommierte Medien wie das New York Times Magazin, Quanta Magazine oder YouTube-Kanäle wie Numberphile bekannt gemacht. Der „Hat“ gehört zu einer Familie von Kacheln, die auch die „Turtle“ einschließt – eine weitere Monotile-Form, die in ähnlicher Weise aperiodisch die Ebene komplett ausfüllt. Das faszinierende an diesen neuen Formen ist nicht nur ihre geometrische Ästhetik, sondern die mathematischen und algorithmischen Herausforderungen, die mit ihrer Untersuchung einhergehen. Um Lösungen zu finden und zu überprüfen, werden zunehmend moderne algorithmische Werkzeuge eingesetzt – allen voran sogenannte SAT-Solver. Diese Programme lösen Probleme der Booleschen Erfüllbarkeit.
Sie können eine Vielzahl von Variablen und komplexen Bedingungen verarbeiten und erlauben damit eine präzise Modellierung von Kachelproblemen. SAT steht für „Satisfiability“, was auf Deutsch „Erfüllbarkeit“ bedeutet. Ein SAT-Solver untersucht, ob es eine Möglichkeit gibt, eine Reihe von Logikbedingungen gleichzeitig zu erfüllen. Die Problemstellung wird dazu in die sogenannte konjunktive Normalform (CNF) gebracht, in der logisch-verknüpfte Variablen in einer standardisierten Struktur angeordnet sind. Vorstellbar ist das etwa so, dass Variablen nur die Werte wahr oder falsch annehmen können, und der Solver prüft, welche Kombination dieser Wahrheitswerte alle vorgegebenen Bedingungen gleichzeitig erfüllt.
Dies macht SAT-Solver zu einem mächtigen Werkzeug für die Lösung kombinatorischer Aufgaben wie Sudoku, Optimierungsprobleme und eben auch das Kacheln der Ebene mit komplizierten Formen wie dem „Hat“ oder der „Turtle“. Die Anwendung von SAT-Solvern im Kontext aperiodischer Tilings ist revolutionär. Ein klassisches Problem in der Flächenkachelung ist die Frage, ob und wie man die Ebene mit bestimmten Formen ohne Überschneidungen und ohne Lücken vollständig zudecken kann. Dabei kommt es häufig darauf an, auch endliche Bereiche mit Kacheln zu befüllen und gleichzeitig bestimmte Einschränkungen einzuhalten. Anwender können komplexe Variablen definieren, die angeben, ob eine Kachel an einer bestimmten Position und in einer bestimmten Orientierung platziert ist.
Etwa gibt es beim „Hat“ insgesamt zwölf Möglichkeiten zur Platzierung an einem Gitternetzpunkt – sechs Rotationen der „Hat“-Form und sechs der spiegelverkehrten „Anti-Hat“-Form. SAT-Solver setzen solche Variablen und Regeln um, um valide Kachelmuster zu finden, die den geometrischen Bedingungen gerecht werden. Die mathematische Eleganz dieser Problemstellung liegt in der Verbindung von Geometrie, Algebra und Informatik. Insbesondere die Umwandlung des geometrischen Kachelproblems in ein Boolesches Modell schafft eine Brücke, die es erlaubt mit Computern komplexe Muster zu analysieren und visuell darzustellen. Die Programmerweiterung und Online-Tools, die solche Solver in einem Browser mittels WebAssembly betreiben, machen die Technologie für eine breite Nutzerschaft zugänglich.
So lassen sich nicht nur Kachelprobleme explorativ lösen, sondern auch beliebige SAT-Probleme in Echtzeit betrachten und testen. Neben dem „Hat“ und der „Turtle“ gibt es eine weitere bemerkenswerte Tile-Form aus derselben Familie, das sogenannte „Spectre“ oder „Tile(1,1)“. Dieses hat die Besonderheit, dass es eine echte chiral aperiodische Monotile darstellt, also ein Element, das die Ebene kontinuierlich und nichtperiodisch kachelt, ohne Kopien seiner Spiegelung zu benötigen. Anders als „Hat“ oder „Turtle“ lebt das „Spectre“ nicht auf einem regulären hexagonalen Gitter und ist auch nicht mehr aus Kites zusammengesetzt. Die zugrundeliegende Theorie ist komplex, doch eine zentrale mathematische Erkenntnis zeigt, dass es sich bei den unterschiedlichen Tiles letztlich um Variationen desselben Grundtyps handelt, wobei die Seitenlängen variiert werden.
Der Clou besteht darin, dass jede aperiodische Kachelung mit „Spectres“ als Deformation von Kachelungen mit „Hats“ und „Turtles“ gedacht werden kann. Diese Beziehung wurde durch eine bahnbrechende mathematische Arbeit von David Smith, Joseph Samuel Myers, Craig S. Kaplan und Chaim Goodman-Strauss belegt. Sie zeigen eine Bijektion zwischen den Tilings mit „Spectres“ und jenen mit „Hat“ und „Turtle“ auf, wodurch Erkenntnisse und Algorithmen für Letztere auch auf den „Spectre“ übertragen werden können. Die komplexen, kombinatorischen Bedingungen für das korrekte Verlegen der Kacheln werden dadurch auf ein beherrschbares Maß reduziert, und es wird möglich, mithilfe der SAT-Solver-Lösungen ganze Muster zu generieren.
Damit können Forscher und Hobby-Anwender spielerisch untersuchen, welche Konfigurationen möglich sind, ob bestimmte Teilmuster in einer vollständigen Kachelung erscheinen oder ausgeschlossen sind. Die Experimente mit der Software sind auch didaktisch wertvoll: Es lassen sich interaktiv die verschiedenen Monotiles platzieren, drehen oder spiegeln, und die SAT-gestützte automatische Lösung füllt die restlichen freien Flächen nach den vorgegebenen Regeln auf. Besonders beeindruckend ist dabei, wie schnell und effizient moderne Laptops oder sogar Smartphones Probleme mit mehreren Millionen logischen Klauseln in überschaubarer Zeit lösen können. Parallel zu diesen Erkenntnissen eröffnen sich auch Einblicke in verwandte Fragestellungen wie der Heesch-Zahl, die angibt, wie oft sich eine Kachelschicht um eine vorhandene Form ohne Lücken und Überlappungen legen lässt. Dieses klassische Problem der Kombinatorik wird mit den gleichen SAT-Techniken bearbeitet und erweitert die theoretische Grundlage der Flächenkachelung grundlegend.
Neben dem rein mathematischen und algorithmischen Zugang bereichert das Thema auch das Feld der visuellen Mathematik und rekreativen Geometrie. Das Interesse an aperiodischen Kachelungen hat in den letzten Jahren enorm zugenommen, nicht zuletzt durch die leicht verständliche Erzählung und die anschaulichen Demonstrationen auf Plattformen unterschiedlicher Art. So tragen Blogs, Videoformate und interaktive Web-Apps dazu bei, komplexe wissenschaftliche Erkenntnisse einer breiteren Öffentlichkeit nahezubringen. Durch die Verfügbarkeit von Open-Source-Code und Online-Tools können Enthusiasten selbst experimentieren, Muster optimieren oder sogar eigene Lösungsansätze mit SAT-Solvern entwickeln. Dies fördert nicht nur die Verbreitung mathematischen Wissens, sondern inspiriert auch zur Anwendung der Technik in ganz anderen Bereichen, etwa in der Kryptographie, der kombinatorischen Optimierung oder beim automatischen Lösen logischer Rätsel wie Sudokus.
Insgesamt zeigt die Entdeckung der „Hut“-Monotile und deren Verwandten, wie tiefgreifend die Zusammenarbeit zwischen traditionellen mathematischen Konzepten und moderner Computertechnologie heute sein kann. SAT-Solver sind dabei nicht nur Spezialwerkzeuge bestimmter Forschungsteams, sondern werden mehr und mehr zu einem allgemein zugänglichen Vehikel, um komplexe logische Strukturen mit Anwendungen über die Mathematik hinaus zu erforschen. Die fortschreitende Entwicklung solcher Algorithmen in Kombination mit spannenden geometrischen Objekten wie dem „Hat“, der „Turtle“ und dem „Spectre“ eröffnet faszinierende Perspektiven für Wissenschaft, Bildung und interaktive Anwendungen. Sie motiviert dazu, komplexe Probleme spielerisch anzugehen, immer neue Fragestellungen zu formulieren und die komplexe Schönheit der Mathematik der Welt zugänglich zu machen.