Durchbruch bei Einweg-Wegeproblemen: Revolutionäre Algorithmen für Single-Source Shortest Paths in gerichteten Graphen

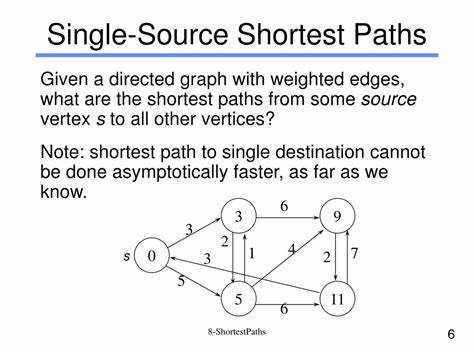
Die Suche nach dem kürzesten Weg in einem Netzwerk ist seit Jahrzehnten ein zentrales Thema in der Algorithmik und Informatik. Von Navigationssystemen über Netzwerkanalyse bis hin zur Optimierung logistischer Prozesse spielt die Berechnung der kürzesten Pfade eine fundamentale Rolle. Insbesondere das Single-Source Shortest Path (SSSP) Problem – die Bestimmung der minimalen Distanzen von einem Startknoten zu allen anderen Knoten in einem gerichteten Graphen – ist eine der wichtigsten Herausforderungen in der Theorie und Praxis. Ein kürzlich erschienener bahnbrechender Forschungsbeitrag bringt nun eine bemerkenswerte Neuerung auf dieses Gebiet: Erstmals konnte die klassische Laufzeitbarriere des beliebten Dijkstra-Algorithmus durchbrochen werden, was eine neue Epoche der effizienten Pfadberechnung einläutet. Der Dijkstra-Algorithmus, entwickelt in den 1950er Jahren, gilt seit jeher als goldener Standard für SSSP-Probleme mit nicht-negativen Kantengewichten.

Sein Algorithmus kombiniert geschickte Prioritätensuche mit entspannenden Kantenupdate-Operationen und erreicht für sparse Graphen typischerweise eine Laufzeit von O(m + n log n), wobei m die Zahl der Kanten und n die Anzahl der Knoten repräsentiert. Trotz zahlreicher Verbesserungen und Varianten sollte man bisher davon ausgehen, dass Dijkstras Ansatz nahezu optimal für das Problem bleibt – insbesondere in der Vergleichs-Addition-Rechenmodell, wo Kantenkosten strikt mit Vergleichen und Additionen behandelt werden. Diese traditionelle Sicht steht nun durch den innovativen Algorithmus von Ran Duan, Jiayi Mao, Xiao Mao, Xinkai Shu und Longhui Yin auf dem Prüfstand. In ihrem Paper „Breaking the Sorting Barrier for Directed Single-Source Shortest Paths“, eingereicht Anfang 2025 an die arXiv-Plattform, beschreiben die Wissenschaftler einen deterministischen Algorithmus mit einer Laufzeit von O(m log^{2/3} n). Diese deutlich verbesserte Laufzeit bricht erstmals die scheinbar unüberwindbare Schranke von Dijkstras Algorithmus für dünn besetzte Graphen.

Das heißt, der neue Algorithmus erreicht in großen, spärlich vernetzten Netzwerken schneller die kürzesten Wege als je zuvor – eine fundamentale Entwicklung für Anwendungen im Bereich der Graphalgorithmen. Die technischen Grundlagen dieser Innovation beruhen auf tiefgreifenden neuen Einsichten in die Struktur gerichteter Graphen und effiziente Datenstrukturen. Herkömmliche Verfahren bauen stark auf Prioritätswarteschlangen auf, die beim Sortieren der Knoten nach Distanz oft zum Flaschenhals werden. Die vorgelegte Methode optimiert diese Sortierprozesse durch intelligente Partitionierung und Komplexitätsreduktion, was die Laufzeit maßgeblich senkt und zugleich eine deterministische Lösung garantiert. Dies ist bemerkenswert, da viele der bisherigen Verbesserungen im SSSP-Bereich entweder randomisiert oder beschränkt auf spezielle Graphenklassen waren.

Die praktischen Implikationen dieses Fortschritts sind weitreichend. Netzwerktechnik, Verkehrsplanung, Robotik und sogar Bioinformatik sind Bereiche, in denen effiziente Berechnung von kürzesten Pfaden essenziell ist. Gerade bei sehr großen, spärlich vernetzten Systemen kann der neue Algorithmus signifikante Leistungssteigerungen ermöglichen. Beispielsweise könnten Navigationssysteme in Echtzeit schneller optimierte Routen berechnen, wohingegen Datenanalyse-Tools komplexe Netzwerkbeziehungen in sozialen oder biologischen Strukturen präziser und rasanter auflösen können. Darüber hinaus entzündet diese Arbeit eine Welle neuer Forschungsideen.

Die Frage, ob die Laufzeit noch weiter verkürzt werden kann, ob dieser Ansatz auf andere graphentheoretische Probleme übertragbar ist oder ob Kombinationsmöglichkeiten mit bereits existierenden Paradigmen bestehen, sind Themen, die aktuell und in nächster Zukunft intensiv untersucht werden. Außerdem bietet die Methode Anknüpfpunkte für eine effizientere Parallelisierung oder Anpassungen für spezielle gewichtete Graphtypen, wie beispielsweise mit negativen oder dynamischen Kantengewichten. Neben der theoretischen Leistung überzeugt auch die Tatsache, dass der Algorithmus deterministisch arbeitet. In Zeiten, in denen Vorhersagbarkeit, Sicherheit und Reproduzierbarkeit zunehmend an Bedeutung gewinnen, bieten solche deterministischen Verfahren Vorteile gegenüber probabilistischen oder randomisierten Methoden, die mit unterschiedlich hoher Erfolgswahrscheinlichkeit arbeiten. So lassen sich beispielsweise Systeme mit garantierter Antwortzeit oder sicherheitskritische Analysewerkzeuge vertrauenswürdiger gestalten.

Interessanterweise zeigt die Forschung auch, dass das altehrwürdige Konzept der Sortierung in Graphalgorithmen nicht mehr zwangsläufig die alles bestim­mende Kostenquelle sein muss. Die intellektuelle Hürde, die mit der sogenannten „Sorting Barrier“ verbunden war, also der angenommenen Minimalgrenze der Berechnungskomplexität verbunden mit Sortiervorgängen, konnte erfolgreich überwunden werden. Diese Erkenntnis könnte andere Bereiche der algorithmischen Forschung beflügeln und neue Denkanstöße für langjährig ungelöste Probleme liefern. Insgesamt markiert die von Duan et al. vorgelegte Entwicklung einen Meilenstein in der algorithmischen Graphentheorie.