Die faszinierende Welt der Gesetze, Potenzgesetze und Statistik In der heutigen Datenwelt, in der Informationen in einem unaufhörlichen Strom fließen, erweist sich die sorgfältige Analyse dieser Daten als entscheidend. Die Wissenschaft hat oft das Bedürfnis, Phänomene und Muster in der Natur zu verstehen und diese durch quantitative Analysen in den Griff zu bekommen. Dabei kommen Gesetze, insbesondere Potenzgesetze, und statistische Methoden ins Spiel. Doch wie verlässlich sind diese Modelle, und welche Gefahren stecken hinter intuitiven Annahmen und fehlerhaften Analysen? Potenzgesetze sind in vielen wissenschaftlichen Disziplinen präsent, von der Physik bis zur Biologie über die Wirtschaftswissenschaften. Ein bekanntes Beispiel ist das Gutenberg-Richter-Gesetz, das in der Geophysik Anwendung findet.
Es beschreibt, dass die Wahrscheinlichkeit für das Auftreten von Erdbeben, die eine bestimmte Energiemenge freisetzen, mit der Energie selbst in umgekehrtem Verhältnis steht, konkret fällt die Wahrscheinlichkeit mit der Energiequadradt ab – also 1/E². Das bedeutet, dass es keine inhärente Skala für Erdbeben gibt, und sie sich über mehrere Größenordnungen erstrecken können. Obwohl solche Gesetze intuitiv und elegant erscheinen, sagt uns die Wahrheit über die dahinterliegenden Daten oft etwas ganz anderes. In der Vergangenheit haben Forscher unzählige Datenanalysen durchgeführt, die zu dem Schluss kamen, dass diese Potenzgesetze die Realität gut widerspiegeln. Die dabei verwendete Methode ist oft einfach: Daten werden in kleine Intervalle eingeteilt, und man zählt die Anzahl der Vorkommen in jedem Bereich.
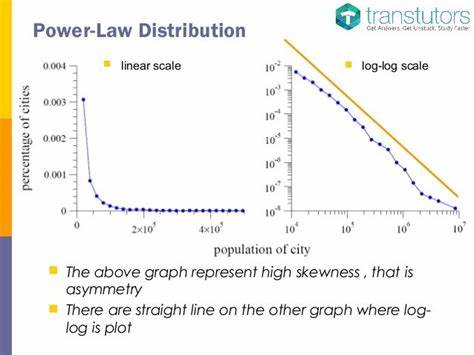
Diese Zählung wird dann in einem Histogramm dargestellt. Potenzgesetze implizieren eine lineare Beziehung in einer log-log-Darstellung der Wahrscheinlichkeit, was bedeutet, dass ein gerader Verlauf auf einen solchen Zusammenhang hinweisen würde. Das Problem dabei ist jedoch, dass der menschliche Geist dazu neigt, in Mustern zu denken, selbst wenn keine echten vorhanden sind. Fortschrittliche statistische Methoden haben oft wenig Beachtung gefunden, während sich viele Autoren auf einfache Regressionstechniken verlassen. Hierbei wird ein linearer Trend in log-transformierte Daten gezwungen, was zu gravierenden Fehlern führen kann.
Das liegt daran, dass traditionelle Regressionstests davon ausgehen, dass die Fehler innerhalb der Daten unabhängig und normalverteilt sind – eine Annahme, die nicht mehr gilt, sobald Daten logarithmisch transformiert werden. Eine spannende Analyse von Clauset und seinen Kollegen hat die Schwierigkeiten und Fallstricke bei der Anwendung dieser Methoden aufgezeigt. Ihre Reanalysen von 24 Datensätzen, die zuvor als Belege für Potenzgesetze angeführt wurden, zeigten, dass die Unterstützung für diese Gesetze stark variieren kann. Während einige Daten wie die Verteilung von Waldbränden und die Anzahl von Weblinks gut mit Potenzgesetzen übereinstimmen, zeigen andere, wie etwa die Verteilung von Wohlstand, nur selten einen solchen Zusammenhang. Die Methode, die Clauset et al.
vorschlagen, um die Wahrscheinlichkeit zu prüfen, dass den Daten ein Potenzgesetz zugrunde liegt, ist relativ einfach und erfordert nur einen moderaten Anstieg der statistischen Kenntnisse. Der erste Schritt besteht darin, die genauen Wahrscheinlichkeiten zu berechnen – eine Technik, die nahezu der Berechnung eines p-Wertes in der regulären Statistik ähnelt. Dies ist entscheidend, um herauszufinden, ob die beobachteten Daten rein zufällig entstanden sein könnten oder ob ein starkes Muster vorhanden ist. Sollte dieses Hypothese-Testverfahren durchfallen, ist es sehr wahrscheinlich, dass die Daten nicht aus einem Potenzgesetz stammen. Wenn sie jedoch bestehen, bedeutet das nicht, dass sie zwangsläufig einem Potenzgesetz folgen.
Der zweite Schritt erfordert dann den Vergleich der Güte der Anpassung zwischen dem Potenzgesetz und anderen potenziellen Verteilungen, wie etwa einer exponentiellen Verteilung oder anderen physikalisch motivierten Verteilungen. Sollte das Potenzgesetz wiederum als das Beste abschneiden, kann es eine plausible Interpretation der Daten darstellen. Ein Beispiel, das man nicht außer Acht lassen sollte, ist die Behauptung, dass die Verteilung von Reichtum weltweit einem Potenzgesetz folgt. Obwohl diese Annahme durchaus populär ist, zeigen umfangreiche Analysen, dass die reale Verteilung deutlich komplexer ist und möglicherweise nicht die einfache Eleganz eines Potenzgesetzes aufweist. Vielmehr könnten Faktoren wie wirtschaftliche Bedingungen, gesellschaftliche Strukturen und politische Einflüsse das Bild der Wohlstandsverteilung prägen.
In der Welt der Wissenschaft ist es wichtig, den Unterschied zwischen einer Hypothese und einer Theorie zu verstehen. Hypothesen sind Annahmen, die getestet werden müssen, während Theorien auf einer umfassenden Menge an empirischen Daten basieren. In vielen Fällen können Forscher in ihrem Bestreben, Erklärungen zu finden, versucht sein, Daten so zu interpretieren, dass sie zu ihren vorgefassten Meinungen passen – ein Phänomen, das als Confirmation Bias bekannt ist. Statistische Methoden bieten eine wichtige Verteidigung gegen solches Wunschdenken. Die Bedeutung einer sorgfältigen Datenanalyse kann nicht hoch genug eingeschätzt werden.
Sie ermöglicht es uns, einen klareren Blick auf die Realität zu werfen und uns von falschen Annahmen zu befreien. Die Statistiken helfen nicht nur, Daten zu interpretieren, sondern fungieren auch als Schutzschild gegen irrationale Denkweisen. Sie lehren uns, die Grenzen unserer Annahmen zu erkennen und uns den Nuancen und der Komplexität weiterführender Analysen zu öffnen. Zusammenfassend lässt sich sagen, dass die Welt der Gesetze, Potenzgesetze und Statistik eine tiefgründige, aber auch herausfordernde ist. Mit dem Wachstum von Big Data in der modernen Gesellschaft ist die Nachfrage nach präzisen statistischen Methoden und Analysen nie zuvor so groß gewesen.
Während die Faszination für Muster und Gesetzmäßigkeiten in der Wissenschaft bestehen bleibt, müssen wir bedachtsam sein und die wesentlichen Konzepte der Datenauswertung und -analyse hinterfragen. Nur so können wir einen echten wissenschaftlichen Fortschritt erzielen und das Verständnis unserer Welt vertiefen.