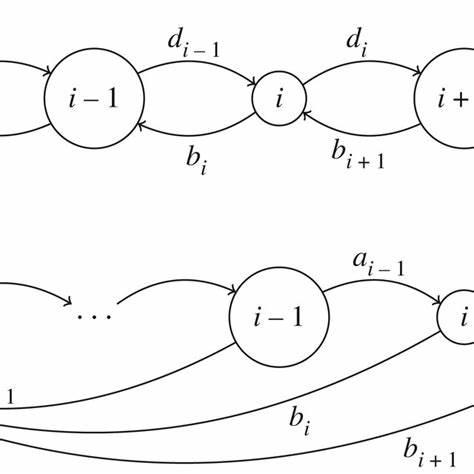
Markow-Ketten sind ein grundlegendes Konzept in der Stochastik und finden breite Anwendung in verschiedenen Bereichen wie Statistik, Physik und natürlich maschinellem Lernen. Besonders relevant sind sie in der Modellierung von Prozessen, die von zufälligen Übergängen zwischen diskreten Zuständen geprägt sind. Während diskrete Markow-Ketten in der Forschung und Praxis weithin bekannt und genutzt werden, sind kontinuierliche Markow-Ketten vielen weniger geläufig. Dennoch spielen diese eine entscheidende Rolle in modernen diskreten Diffusionsmodellen, die zunehmend in der künstlichen Intelligenz und Datenverarbeitung eingesetzt werden. Eine Markow-Kette ist ein stochastischer Prozess, der durch zwei wesentliche Eigenschaften gekennzeichnet wird: Die Zustände sind diskret, das heißt, die Zufallsvariablen des Prozesses nehmen Werte aus einer endlichen oder abzählbaren Menge an, und der Prozess erfüllt die Gedächtnislosigkeit oder Markow-Eigenschaft.
Diese besagt, dass die Zukunft des Prozesses nur vom gegenwärtigen Zustand abhängt und unabhängig von der Vergangenheit ist. Mathematisch formuliert bedeutet dies, dass die Zufallsvariablen zu unterschiedlichen Zeitpunkten t sich so verhalten, dass die Wahrscheinlichkeit eines zukünftigen Ereignisses nur vom aktuellen Zustand beeinflusst wird. Im Rahmen der Markow-Ketten unterscheidet man zwischen diskreter und kontinuierlicher Zeit. Bei diskreter Zeit erfolgt der Übergang zwischen Zuständen in festgelegten Zeitschritten, beispielsweise in ganzen Zahlen. Die Kenngröße hier ist die Übergangsmatrix, die für jeden Zeitpunkt die Wahrscheinlichkeiten beschreibt, von einem Zustand in einen anderen zu wechseln.
Diese Matrix kann zeitlich variieren oder konstant sein. Bei Konstanz spricht man von einer homogenen Markow-Kette. Der Schritt zur kontinuierlichen Zeit ist nicht einfach ein fließendes Erweiteren des diskreten Modells. Hier ersetzt man die festen Zeitschritte durch eine kontinuierliche Zeitachse. Statt mit einer Übergangsmatrix zu arbeiten, wird der Prozess durch eine sogenannte Rate-Matrix beschrieben.
Diese enthält positive Werte, die als Parameter der Exponentialverteilung dienen und die Intensität beziehungsweise Geschwindigkeit der Zustandswechsel in der Kette angeben. Ein anschaulicher Weg, sich eine kontinuierliche Markow-Kette vorzustellen, führt über das Konzept der Wartezeiten. In einer homogenen diskreten Markow-Kette bleibt der Prozess in einem Zustand für eine Anzahl von Schritten, die einer geometrischen Verteilung folgt. Die geometrische Verteilung besitzt eine einzigartige Gedächtnislosigkeit: Die Wahrscheinlichkeit, dass das Ereignis zu einem späteren Zeitpunkt eintritt, hängt nicht davon ab, wie lange bisher gewartet wurde. Diese Eigenschaft ist essentiell, um die Markow-Eigenschaft zu bewahren.
Für die Erweiterung in die kontinuierliche Zeit ersetzt man diese geometrische Verteilung durch die Exponentialverteilung, welche ebenfalls gedächtnislos ist. Das bedeutet, in einem kontinuierlichen Markow-Prozess verbleibt der Prozess in einem Zustand für eine Zeit, die einer Exponentialverteilung mit einem spezifischen Parameter entspricht, bevor er zu einem anderen Zustand übergeht. Das macht die Exponentialverteilung zur einzigen geeigneten Wahl, um den Prozess ohne Gedächtnisverlust auf kontinuierliche Zeit zu übertragen. Die Rate-Matrix definiert dabei die Übergangsraten zwischen den Zuständen. Anders als bei den Übergangswahrscheinlichkeiten in diskreter Zeit, sind diese Werte nicht notwendigerweise eine Wahrscheinlichkeit, sondern positive Werte, die das erwartete Verhalten der Wartezeiten steuern.
Diese Matrix ermöglicht die Berechnung von Wahrscheinlichkeiten für Zustandsänderungen über beliebig kleine Zeitintervalle und bildet die mathematische Grundlage für die kontinuierlichen Markow-Ketten. Die Anwendung von kontinuierlichen Markow-Ketten ist vor allem dann interessant, wenn Übergänge nicht nur zu festen Zeitpunkten erfolgen, sondern zu zufälligen und potenziell sehr kurzen oder langen Zeiten. Gerade in der Modellierung von diskreten Diffusionsprozessen, wie sie beispielsweise in der aktuellen Forschung im maschinellen Lernen vorkommen, sind kontinuierliche Markow-Ketten von zentraler Bedeutung. Sie erlauben die realistischere Beschreibung zeitlich hybrider und dynamischer Prozesse in der Datenverarbeitung. Nicht-homogene Markow-Ketten, bei denen sich die Übergangsraten im Laufe der Zeit ändern, werfen besondere Herausforderungen auf.
Die einfache Exponential-Verteilungsannahme für Wartezeiten gilt hier nicht mehr uneingeschränkt. Stattdessen wird der Prozess komplexer und muss häufig mit Hilfe von Punktprozessen beschrieben werden, welche der Theorie nach Ereignisse auf der Zeitachse modellieren. Punktprozesse sind mathematische Modelle für Ereignisfolgen, die zufällig über eine Zeitachse verteilt sind. Sie können diskret oder kontinuierlich definiert sein. Im diskreten Fall ist beispielsweise das Bernoulli-Schema bekannt, während kontinuierliche Varianten, wie der Poisson-Punktprozess, eine natürliche Erweiterung darstellen.
Diese Prozesse besitzen eine enge Verbindung zu Markow-Ketten, insbesondere, weil Wartezeiten und Zustandsübergänge oft durch Ereignisse in Punktprozessen repräsentiert werden können. Die Beziehung zwischen Punktprozessen und Markow-Ketten lässt sich illustrieren durch das Beispiel eines Hasen, der in einem Garten Ostereier versteckt. Verschiedene Modelle können beschreiben, wie der Hase die Eier verteilt: ob in diskreten Schritten nach einem Bernoulli-Schema, über Geometrisch verteilte Pausen oder durch zufällige, uniform verteilte Plätze. Im Grenzfall, wenn der Garten als kontinuierlicher Raum betrachtet wird, führt dies zu einem homogenen Poisson-Punktprozess, der die Anordnung der Ereignisse (Eier) beschreibt. Dieses Verständnis öffnet auch die Tür zur Simulation von kontinuierlichen Markow-Ketten mittels Punktprozessen.
Für jede möglichen Zustandsübergang existiert ein eigener Punktprozess, der Ereignisse an zufälligen Zeitpunkten generiert. Durch Auswahl des frühesten Ereignisses aus diesen Prozessen lässt sich der zugehörige Zustandsübergang bestimmen. Damit wird der Pfad des Markow-Prozesses im Zeitverlauf konstruiert. Eine der faszinierenden Eigenschaften dieses Ansatzes ist, dass viele der erzeugten Ereignisse tatsächlich nicht zu einem Zustandswechsel führen, da sie nicht die frühesten in ihrem Zustand sind. Dennoch ermöglicht diese redundante Darstellung eine flexible Erweiterung auf nicht-homogene Markow-Ketten, bei denen die Übergangsraten von der Zeit abhängen.
Hier kommen zeitabhängige Punktprozesse ins Spiel, die eine dynamischere Modellierung erlauben. In der Praxis eröffnen kontinuierliche Markow-Ketten spannende Möglichkeiten, beispielsweise bei der Modellierung sequenzieller Daten, Zustandserkennung in dynamischen Systemen oder der Entwicklung effizienter Algorithmen im maschinellen Lernen wie bei Diffusionsmodellen. Gerade die Fähigkeit, Wartezeiten und Übergänge realistisch und zeitkontinuierlich abzubilden, führt zu genaueren und oft rechenmäßig eleganteren Methoden. Zusammenfassend lässt sich sagen, dass kontinuierliche Markow-Ketten eine natürliche Erweiterung der bekannten diskreten Modelle darstellen und mit ihrem Bezug zur Exponentialverteilung und Punktprozessen tiefe mathematische Strukturen offenbaren. Für Forscher und Praktiker, die mit stochastischen Prozessen arbeiten, sind sie ein unverzichtbares Werkzeug, das nicht nur theoretisch interessant ist, sondern auch eine breite Palette moderner Anwendungen ermöglicht.
Die Kombination aus Wartezeitmodellierung, Punktprozessen und dynamischen Übergangsraten macht sie zu einem Schlüsselkonzept für die Zukunft der diskreten Diffusion und darüber hinaus.