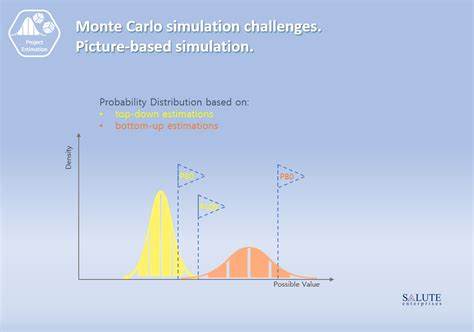
Monte-Carlo-Simulationen haben sich seit Jahrzehnten als eine wertvolle Methode zur Bewertung von Unsicherheit und Stochastik in unterschiedlichsten Fachbereichen etabliert. Ob in der Finanzanalyse, Risikobewertung, Physik oder Technik: Die Grundidee, durch Zufallsstichproben eine numerische Approximation eines komplexen Problems zu erlangen, ist intuitiv und leistungsfähig. Doch trotz dieser Vorteile gibt es viele Szenarien, in denen Monte-Carlo-Simulationen als wenig attraktiv empfunden werden – sei es wegen ihres Rechenaufwands, der Ungenauigkeit oder der fehlenden Transparenz im Ergebnis. Im Folgenden werden die zentralen Kritikpunkte und Herausforderungen dieser Methode erläutert, um ein umfassendes Verständnis zu vermitteln. Monte-Carlo-Simulationen beruhen darauf, eine Vielzahl zufälliger Ausprägungen innerhalb eines Modells zu generieren und daraus statistische Kennwerte zu berechnen.
Diese Herangehensweise ist besonders dann sinnvoll, wenn das zugrunde liegende mathematische Modell analytisch oder deterministisch schwer lösbar ist. Allerdings bringen gerade diese zahlreichen Simulationen einen hohen Rechenaufwand mit sich. Computer müssen Tausende oder Millionen von Iterationen durchlaufen, um repräsentative Aussagen treffen zu können. Dies führt gerade bei komplexen, mehrdimensionalen Problemen zu großen Anforderungen an Hard- und Software. In vielen betrieblichen oder alltäglichen Situationen sind solche Ressourcen schlicht nicht vorhanden oder nicht wirtschaftlich einsetzbar.
Hinzu kommt, dass die Genauigkeit der Ergebnisse in direktem Zusammenhang mit der Anzahl der Simulationen steht. Für eine ausreichend hohe Genauigkeit müssen große Stichproben genommen werden, was die Rechenzeit exponentiell erhöht. Monte-Carlo-Methoden konvergieren oft langsam, was bedeutet, dass die resultierenden Schätzungen nur mit einer gewissen Unsicherheit belastet sind. Für Entscheidungsträger ist das problematisch, denn eine unsichere oder vage Prognose erschwert belastbare Handlungen. Dieser Mangel an Präzision macht Monte-Carlo-Simulationen insbesondere dann weniger attraktiv, wenn schnelle und genaue Entscheidungen gefragt sind.
Kritiker bemängeln außerdem die fehlende Transparenz und Nachvollziehbarkeit der Ergebnisse. Anders als klassische analytische Methoden erlauben Monte-Carlo-Simulationen oft keine klare Einsicht, wie einzelne Variablen oder Zusammenhänge die Resultate beeinflussen. Der stochastische Charakter lässt sich nur schwer nachvollziehen und kommunizieren, was insbesondere in regulierten Branchen oder in der Zusammenarbeit mit nicht-technischen Partnern problematisch sein kann. Diese Schwierigkeit behindert häufig das Vertrauen in die Methode und ihre Akzeptanz bei Stakeholdern. Darüber hinaus erfordern Monte-Carlo-Ansätze eine zuverlässige Modellierung und valide Eingangsgrößen.
Werden diese Ausgangsdaten falsch gewählt oder unvollständig erfasst, führen die Simulationen zu fehlerhaften oder irreführenden Ergebnissen. Insbesondere bei sensiblen oder kritischen Anwendungen kann eine solche Abhängigkeit von Eingangsparametern fatale Folgen nach sich ziehen. Aufgrund dieses Risikos sind Monte-Carlo-Methoden in manchen Kontexten daher mit Vorsicht zu genießen. Nicht zuletzt kann auch die theoretische Komplexität der Monte-Carlo-Simulationen zur Abschreckung führen. Eine fundierte Anwendung setzt Fachwissen in Statistik, Programmierung und Domänenkenntnis voraus.
Für viele Anwender ohne entsprechende Ausbildung ist der Einstieg schwierig und die Gefahr von Fehlbedienung oder Fehlinterpretation groß. Dies verhindert einen breiteren und unkomplizierten Einsatz in der Praxis. Die Vielseitigkeit von Monte-Carlo-Methoden ist zugleich ihre Stärke und Schwäche. Modularität, Anpassbarkeit und die Fähigkeit zur Einbeziehung beliebiger Wahrscheinlichkeitsverteilungen machen sie mächtig, doch genau diese Flexibilität führt zu einem großen Potenzial an Fehlerquellen und dem Bedarf an sorgfältiger Planung und Kontrolle. In Bereichen, wo schnelle Ergebnisse und hohe Verlässlichkeit entscheidend sind, werden oft alternative Methoden bevorzugt.
Dazu zählen deterministische Simulationen, analytische Lösungen oder heuristische Verfahren, die weniger rechenintensiv sind und eine klarere Interpretation erlauben. Besonders in der Finanzwelt, wo Monte-Carlo-Simulationen weit verbreitet sind, greifen Marktteilnehmer zum Beispiel auf Szenarioanalysen oder Closed-Form-Modelle zurück, wenn Zeit oder Ressourcen limitiert sind. Trotz der genannten Nachteile sind Monte-Carlo-Simulationen jedoch keineswegs obsolet. Sie bleiben ein unverzichtbares Werkzeug vor allem bei sehr komplexen Fragestellungen und bei der Analyse von Risiken mit komplexer Wahrscheinlichkeitsverteilung. Ihre Fähigkeit, auch mit unvollständigen Informationen realistische Prognosen zu erstellen, ist einzigartig.
Für eine bessere Attraktivität wird jedoch an Verbesserungen geforscht. So erhöhen moderne Ansätze wie Quasi-Monte-Carlo oder adaptive Sampling die Konvergenzgeschwindigkeit und reduzieren die Rechenzeit erheblich. Fortschritte in Hardware, beispielsweise Throughput-optimierte GPUs, ermöglichen zudem die Durchführung einer größeren Anzahl Simulationen in kürzerer Zeit. Für Praktiker ist es daher wichtig, die Limitationen von Monte-Carlo-Simulationen zu kennen und den Einsatz gezielt abzuwägen. Ein sinnvolles Vorgehen umfasst oft die Kombination mehrerer Methoden oder die Verwendung von Monte-Carlo nur in ausgewählten Phasen eines Modells.
Gleichzeitig sollten Maßnahmen zur Sicherstellung der Datenqualität und zur transparenten Kommunikation der Unsicherheiten implementiert werden. Abschließend lässt sich sagen, dass Monte-Carlo-Simulationen aufgrund ihrer Rechenintensität, langsamen Konvergenz, fehlenden Transparenz und Abhängigkeit von präzisen Eingangsdaten in vielen Situationen als weniger attraktiv gelten. Trotzdem bieten sie unverzichtbare Vorteile bei der Analyse komplexer stochastischer Systeme. Die fortschreitende technologische Entwicklung und methodische Innovationen versprechen, einige der heutigen Schwächen zu überwinden und die Attraktivität dieser Verfahren in Zukunft zu steigern.