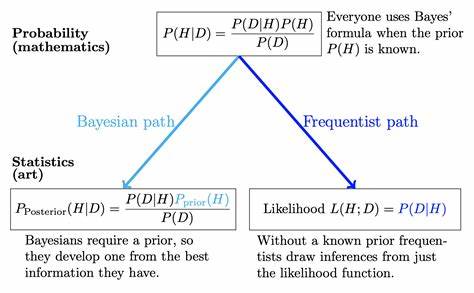
In der Welt der Statistik treffen Forscher und Datenanalysten häufig auf zwei dominierende Paradigmen, die trotz ihrer zentralen Bedeutung oft miteinander verwechselt werden oder nicht vollständig verstanden sind: der Frequentismus und der Bayesianismus. Beide Ansätze bieten unterschiedliche Sichtweisen auf das Verständnis von Wahrscheinlichkeit und führen zu verschiedenen Methoden der Datenanalyse. Um fundierte Entscheidungen in Wissenschaft, Technik und Wirtschaft treffen zu können, ist es daher essenziell, die jeweiligen Prinzipien und praktischen Anwendungsmöglichkeiten dieser beiden Konzepte zu kennen und zu verstehen. Der Frequentismus definiert Wahrscheinlichkeit als den Grenzwert der relativen Häufigkeit eines Ereignisses bei unendlich häufigen Wiederholungen eines Experiments. In diesem Kontext ist ein Ereignis lediglich eine beobachtbare Ausprägung dessen, was unter konstanten Bedingungen immer wieder gemessen oder beobachtet wird.
Aus Sicht des Frequentisten gibt es keine sinnvolle Definition der Wahrscheinlichkeit eines unbekannten, aber festen Parameters – etwa der tatsächlichen Helligkeit eines Sterns – da dieser Parameter per Definition einen festen Wert hat, der nicht variabel ist. Die Wahrscheinlichkeit beschreibt also ausschließlich die Verteilung der Messwerte, nicht die Unsicherheit über den Parameter selbst. Bayesianismus hingegen erweitert den Begriff der Wahrscheinlichkeit auf das Maß der Überzeugung oder des Wissens über eine Aussage. Prozentuale Wahrscheinlichkeiten quantifizieren somit das subjektive Vertrauen, das man in eine bestimmte Hypothese oder einen Parameter hat. Dies impliziert, dass man durchaus Sinn darin sieht, von der Wahrscheinlichkeit des wahren Werts eines Parameters zu sprechen.
Die Wahrscheinlichkeit verknüpft das bisherige Wissen (Priorwissen) mit neu eingehenden Daten, um eine aktualisierte Einschätzung (Posterior) zu liefern. Dadurch erlaubt die bayesianische Statistik eine flexible Einbindung von Vorwissen und eine kontinuierliche Aktualisierung, was sie besonders in komplexen oder datenarmen Szenarien praktisch wertvoll macht. Die philosophischen Differenzen zwischen diesen beiden Sichtweisen führen zu unterschiedlichen Vorgehensweisen bei der statistischen Datenanalyse. Während der Frequentist häufig auf Maximum-Likelihood-Schätzungen setzt, die einen einzigen Schätzwert mit zugehöriger Fehlerabschätzung liefern, ermittelt der Bayesianer die gesamte Wahrscheinlichkeitsverteilung der Parameter, häufig über iterative Algorithmen wie Markov Chain Monte Carlo (MCMC). Trotz dieser Unterschiede führen beide Ansätze bei einfachen Problemen oftmals zu sehr ähnlichen Ergebnissen.
Der Unterschied wird vor allem bei komplexeren Modellen und Datenstrukturen offensichtlich. Ein immer wieder genutztes Beispiel zur Veranschaulichung ist die Messung von Photonenzählungen bei der Beobachtung eines Sterns. Angenommen, es werden mehrfach Messungen des Photonenzählflusses durch ein Teleskop durchgeführt, wobei für jede Messung ein Wert und eine zugehörige Unsicherheit erfasst werden. Der Frequentist würde in diesem Fall den Mittelwert der Beobachtungen berechnen, gewichtet nach der Inverse der quadrierten Fehler, um den wahrscheinlichsten wahren Wert zu schätzen. Die Unsicherheit des Schätzers lässt sich unter der Annahme normalverteilter Fehler ebenfalls berechnen.
Im bayesianischen Rahmen wird dagegen die gesamte Wahrscheinlichkeitsverteilung für den zu schätzenden Parameter basierend auf einem nicht-informativen oder informativen Prior berechnet. Dabei wird die Likelihood-Funktion mit dem Prior multipliziert und gemäß Bayes' Theorem normalisiert. Praktisch geschieht dies häufig über MCMC-Methoden, welche eine repräsentative Stichprobe aus dem Posterior erzeugen. Ein Vorteil der bayesianischen Methode ist ihre Fähigkeit, explizit Priorwissen zu integrieren und somit in bestimmten Situationen präzisere oder robustere Schätzungen zu ermöglichen. Bei der Betrachtung von Photonenzählungen, die einer Poisson-Verteilung folgen, zeigt sich, dass bei einfachen Modellen und ausreichender Datenmenge die beiden Ansätze häufig zu fast identischen Einschätzungen kommen.
Die bayesianische Methode erfordert allerdings mehr Rechenaufwand und ist daher in einfachen Szenarien möglicherweise weniger effizient. Dennoch bietet sie den entscheidenden Vorteil, dass sie ohne die üblichen frequentistischen Beschränkungen, etwa der Notwendigkeit großer Stichproben, auskommt. Wird das Modell jedoch komplexer, beispielsweise wenn angenommen wird, dass der Stern fluxvariabel ist, so steigen die Anforderungen an die Modellierung. Ein zweidimensionaler Parameterraum mit Mittelwert und intrinsischer Streuung des Sternenflusses erfordert numerische Verfahren zur Auswertung sowohl bei Frequentisten als auch bei Bayesians. Hier zeigt sich deutlich, wie MCMC-Methoden es ermöglichen, die Posteriorverteilung vollständig zu erfassen, während frequentistische Verfahren wie die Maximum-Likelihood-Schätzung oft auf numerische Optimierung und Bootstrap-Techniken zurückgreifen, um Unsicherheiten abzuschätzen.
Die Bayesianer betonen, dass die Wahl des Priors zwar subjektiv sein kann, die explizite Berücksichtigung dieser Subjektivität jedoch einem robusteren und transparenteren Umgang mit Unsicherheiten dient. Die Frequentisten erwidern, dass das Fehlen von subjektiven Elementen in ihrem Ansatz dem wissenschaftlichen Ideal der Objektivität näherkommt. Tatsächlich lässt sich Frequentismus aber oftmals als Spezialfall des Bayesianismus interpretieren, nämlich als Bayes-Analyse mit einem nicht-informativen, oft implizit angenommenen Prior. In der praktischen Anwendung werden beide Ansätze häufig kombiniert. Beispielsweise kann ein Forscher zunächst eine bayesianische Analyse mit MCMC durchführen, um die volle Posteriorverteilung zu erhalten, und anschließend frequentistische Methoden nutzen, um Parameterwerte und Unsicherheiten zu summarisch zu beschreiben.
Besonders bei multidimensionalen Problemen, wie der Schätzung von astronomischen Parametern oder der Modellierung komplexer physikalischer Prozesse, sind bayesianische Verfahren in Kombination mit modernen Algorithmen wie emcee sehr mächtig. Diese ermöglichen es, chaotische oder nicht-normalverteilte Posterioren abzubilden – ein Szenario, das bei standardfrequentistischen Methoden oft problematisch ist. Die offensichtliche Stärke der Bayesianer liegt in der erweiterten Ausdrucksfähigkeit und Flexibilität ihres Ansatzes, gerade bei Einbeziehung von Vorwissen oder bei komplexen Daten. Frequentisten profitieren hingegen von einfacheren Verfahren, die bei großen Datenmengen oft ausreichend genau und effizient sind. Beide Perspektiven ergänzen sich und tragen auf ihre Weise zur Qualitätssteigerung wissenschaftlicher Erkenntnisse bei.
Insbesondere im Zeitalter großer Datensätze und komplexer Modellstrukturen, etwa in den Bereichen Astronomie, Medizin oder maschinelles Lernen, lohnt es sich, beide Paradigmen zu kennen. So können Forscher situativ entscheiden, ob der Einsatz von Priors sinnvoll ist, ob komplexe Posteriors durch MCMC exploriert werden sollten oder ob eine klassische Maximum-Likelihood-Schätzung ausreichend ist. Ein weiterer relevanter Aspekt ist die Interpretation statistischer Resultate. Während Frequentisten in der Regel Punktwerte mit Konfidenzintervallen angeben, interpretiert der Bayesianer diese Intervalle als Glaubwürdigkeitsbereiche. Diese sind intuitiv verständlicher, da sie direkt die Wahrscheinlichkeit angeben, dass der wahre Wert innerhalb eines bestimmten Bereichs liegt, wohingegen Frequentisten Konfidenzintervalle als langfristigen Erwartungswert bei Wiederholungen interpretieren.
In der Praxis findet man auch immer wieder hybride Ansätze, die Elemente beider Denkschulen kombinieren oder pragmatisch auswählen, je nachdem, welcher Effekt dominanter ist. Wichtig bleibt jedoch, sich stets der unterschiedlichen philosophischen Grundlagen bewusst zu sein, um Analyseergebnisse korrekt interpretieren und kommunizieren zu können. Ein umfangreiches Verständnis sowohl der theoretischen als auch der praktischen Unterschiede eröffnet Anwendern nicht nur eine größere Werkzeugpalette, sondern fördert auch den kritischen Umgang mit statistischen Verfahren. Die Integration von Python-basierten Beispielen, wie sie in der Implementierung von Paketem wie SciPy, astroML oder emcee gezeigt werden, erleichtert zudem die Anwendbarkeit der Methoden in aktuellen Forschungsszenarien. Zusammenfassend lässt sich festhalten, dass Frequentismus und Bayesianismus grundlegende unterschiedliche Auffassungen von Wahrscheinlichkeit und Statistik repräsentieren, die jeweils ihre spezifischen Stärken und Herausforderungen haben.
Während die Aufgabenstellung und die verfügbare Datenmenge nicht selten die Wahl des statistischen Ansatzes beeinflussen, sind beide Methoden gebräuchlich und können in vielen Fällen komplementär eingesetzt werden. Die Fähigkeit, beide Methoden zu verstehen und praktisch anzuwenden, ist eine wichtige Kompetenz moderner Wissenschaftler und Datenexperten.