Wenn gute Pseudozufallszahlen versagen: Die Tücken der multivariaten Normalverteilung in der Statistik

Analyse des Kryptomarkts

Pseudorandomzahlen sind das Herzstück zahlreicher statistischer Verfahren und Simulationen. Mit ihrer Hilfe können komplexe Modelle nachvollziehbar und wiederholbar gemacht werden – vorausgesetzt, man versteht die Tücken, die sich bei ihrer Verwendung verbergen. Besonders bei der Erzeugung von Stichproben aus multivariaten Normalverteilungen zeigen sich schwerwiegende Probleme, welche die Erwartung von Reproduzierbarkeit erschüttern. Das Problem beginnt oft harmlos. Ein Forscher oder Datenwissenschaftler setzt einen festen Startwert für den Zufallszahlengenerator, nutzt eine etablierte Funktion in R oder einer anderen Programmiersprache und erwartet, dass bei erneutem Ausführen derselben Funktion auf verschiedenen Rechnern identische Ergebnisse entstehen.

Doch genau das erweist sich im Fall multivariat normalverteilter Stichproben häufig als Illusion. Trotz Verwendung von set.seed() und anderen Maßnahmen generieren verschiedene Systeme unterschiedliche Daten – und das nicht nur in minimalem Ausmaß, sondern teils gravierend abweichend. Diese Situation findet ihre Ursache in der diskreten und begrenzten Darstellung von Zahlen im Computer, bekannt als Floating-Point-Arithmetik. Anders als in der Mathematik gibt es hier keine ideale Welt der Zahlen, sondern einen Raum voller Trunkierungsfehler und Rundungsungenauigkeiten, die sich im Verlauf komplexer Berechnungen vervielfältigen können.

Besonders Matrixoperationen, die essenziell für die Konstruktion multivariater Stichproben sind, leiden darunter. Das Kernproblem liegt in der Zerlegung von Kovarianzmatrizen. Zur Erzeugung einer multivariat normalverteilten Zufallsstichprobe benötigt man eine Zerlegung der Kovarianzmatrix, etwa in Form einer Eigenwertzerlegung oder einer Cholesky-Dekomposition. Wird dafür die Eigenwertzerlegung verwendet, liefert dieselbe Kovarianzmatrix auf unterschiedlichen Rechnern durchaus verschiedene Eigenvektoren, obwohl die Eigenwerte übereinstimmen. Diese Unterschiede treten bereits bei geringfügigen Abweichungen der Matrixwerte auf, etwa durch minimale Floating-Point-Fehler.

Die Folge ist, dass die verwendete Transformation, die eine Standardnormalverteilung in eine multivariate Normalverteilung überführt, auf verschiedenen Rechnern drastisch divergiert. Das Resultat sind Zufallszahlen, die zwar statistisch korrekt verteilt sind, aber eben nicht reproduzierbar. Man hat also mit einer Situation zu kämpfen, in der der statistische Algorithmus formal richtig arbeitet, die Ergebnisse aber in ihrer numerischen Ausprägung radikal voneinander abweichen. Die naheliegende und praktikable Alternative zur Eigenwertzerlegung stellt die Cholesky-Zerlegung dar. Sie liefert eine eindeutigere und stabilere Zerlegung mit positiv definierten Diagonalwerten, was die numerische Reproduzierbarkeit deutlich verbessert.

Zwar sind auch hier gewisse Floating-Point-Fehler unvermeidbar, die signifikanten Verfälschungen, wie sie bei der Eigenwertzerlegung auftreten können, werden aber stark reduziert. Darüber hinaus setzen professionelle Implementierungen moderner Statistikpakete, wie etwa mvtnorm in R, auf zusätzliche Strategien zur Verbesserung der numerischen Stabilität. Eine solche Technik besteht darin, die Transformation so zu definieren, dass mögliche Vorzeichenwechsel der Eigenvektoren durch die Floating-Point-Arithmetik keinen Einfluss auf das endgültige Ergebnis haben. Dieser Ansatz macht die Berechnung deutlich robuster gegenüber subtilen numerischen Schwankungen. Ein weiteres häufig übersehenes Problem im Kontext multivariater Normalstichproben ist die Art und Weise, wie Zufallszahlen organisiert werden.

Während intuitive Erwartungshaltungen nahelegen, dass zusätzliche Stichproben einfach angefügt werden, ohne vorherige Werte zu verändern, nutzen einige ältere Funktionen wie MASS::mvrnorm() die generierten Zufallszahlen spaltenweise anstatt zeilenweise. Dies führt dazu, dass das Hinzufügen einer neuen Stichprobe zuvor generierte Werte verändert, was die Reproduzierbarkeit in komplexen Simulationen zusätzlich erschwert. Nun könnte man meinen, diese Schwierigkeiten ließen sich durch verbesserte Hard- oder Software lösen. Tatsächlich wäre eine bit-genaue Reproduzierbarkeit über unterschiedliche Rechner und Umgebungen theoretisch möglich, erfordert aber enormen Mehraufwand, der sich in Form von massiv längeren Rechenzeiten und erhöhtem Ressourceneinsatz bemerkbar macht. Insbesondere in angewandten Wissenschaften ist ein solches Vorgehen meist nicht praktikabel oder wirtschaftlich vertretbar.

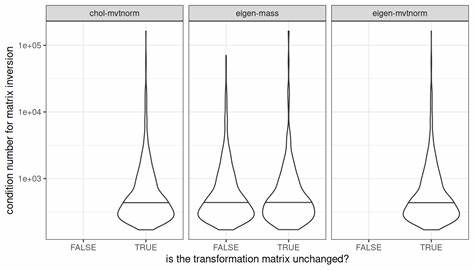
Ein weiterer verbreiteter Fehler ist die Überschätzung des Werts von Konditionszahlen. Die Konditionszahl einer Matrix beschreibt grob, wie sensitiv ein Problem auf kleine Änderungen der Eingabedaten reagiert. Häufig wird sie als Indikator für numerische Stabilität herangezogen. Im Zusammenhang mit multivariater Normalverteilung sollte man allerdings vorsichtig sein. Die Konditionszahl, bezogen auf die Matrixinversion, ist ein Parameter, der vorwiegend für andere Berechnungen relevant ist.

Für die Eigenwertzerlegung oder die Cholesky-Zerlegung und das Sampling aus multivariaten Verteilungen kann sie dagegen wenig aussagen. In der Praxis empfiehlt es sich, stets das Samplingverfahren und dessen numerische Stabilität in einem eigenen Kontext zu betrachten. Das Verwenden aktuell gepflegter und weiterentwickelter Softwarepakete ist hier ein zentraler Punkt, ebenso wie das bewusste Setzen von Zufallszahlengeneratorsaatwerten unmittelbar vor den relevanten Operationen. Für Anwender statistischer Software bedeutet dies auch, dass ein „einfaches“ Setzen des Seed-Werts nicht immer automatische Reproduzierbarkeit garantiert. Gerade bei relevanten Simulationen sollten deshalb Ergebnisse kritisch hinterfragt, mit unterschiedlichen Methoden überprüft und möglichst mit robusten Implementierungen arbeitend getestet werden.

Eine gute Praxis ist zudem, sich grundlegende Prinzipien der numerischen Mathematik anzueignen. Die Kenntnis darüber, wie Floating-Point-Arithmetik funktioniert, welche Typen von Matrixzerlegungen es gibt und wie sich diese mathematisch verhalten, ermöglicht fundiertes Verständnis und besseres Troubleshooting. Auch wenn diese Themen auf den ersten Blick trocken oder komplex erscheinen, lohnt sich der Aufwand langfristig, um unerwartete Fehlerquellen schnell identifizieren und beheben zu können. Reproduzierbarkeit ist in der heutigen wissenschaftlichen Arbeit zentral. Wissenschaftler, Entwicklern und Datenanalysten ist bewusst, wie kritisch es sein kann, wenn ein Experiment oder eine Analyse nicht reproduzierbar ist.

Auch wenn Floating-Point-Fehler zwangsläufig sind, lassen sich durch kluge Wahl der Methoden und Softwarepakete Fehlerquellen minimieren und die Reproduzierbarkeit der Simulationen sicherstellen. Zusammenfassend lässt sich festhalten, dass die Erzeugung multivariater Normalstichproben als zentraler Baustein in vielen datenwissenschaftlichen und statistischen Anwendungen keinesfalls trivial ist. Die technische Realität der Computerarithmetik führt zu Herausforderungen, die selbst bei scheinbar sorgfältiger Anwendung Standardmethoden aus der Bahn werfen können. Glücklicherweise existieren inzwischen praktikable Lösungen, die sowohl numerisch stabiler sind als auch bessere Reproduzierbarkeit garantieren. Zu diesen zählen der Einsatz der Cholesky-Zerlegung kombiniert mit robusten Algorithmen zur Zufallszahlerzeugung sowie bewährte Softwarebibliotheken, welche diese Verfahren integriert bereitstellen.

Eine bewusste Handhabung der Seed-Einstellung, die Positionierung dieser in den Codeabschnitten sowie die Auswahl von Sampling-Methoden sind essenziell, um unerwartete Überraschungen im Ergebnis zu vermeiden. Der Blick für die zugrunde liegenden mathematischen und numerischen Prinzipien hilft hier maßgeblich und macht den Unterschied zwischen einem robusten und einem instabilen Analyseprozess aus. Dies macht deutlich, dass ein tieferes Verständnis der Implementierungsdetails und der zugrundeliegenden Numerik nicht nur etwas für Spezialisten ist, sondern eine wichtige Kompetenz für alle, die sich ernsthaft mit statistischen Simulationen und deren Reproduzierbarkeit beschäftigen wollen. An dieser Stelle sollte auch der pragmatische Hinweis stehen, dass jegliche methodische Verbesserung immer auch abgewogen werden muss gegen die Anforderungen an Geschwindigkeit und Ressourcen – so lautet die Realität im datengetriebenen Arbeiten. Abschließend gilt: bei der Arbeit mit Pseudozufallszahlen und insbesondere bei der Generierung multivariater normalverteilter Stichproben ist Vorsicht angebracht.

Die Illusion, dass ein Seed immer gleichbleibende Ergebnisse garantiert, ist trügerisch. Ein fundiertes Wissen über Floating-Point-Arithmetik, Matrixzerlegungen und ihre Auswirkungen auf die Stabilität kann helfen, den richtigen Umgang mit diesen Problemen zu finden. Professionelle Statistikbibliotheken nehmen den Nutzern viel Arbeit ab, sind aber nicht frei von Grenzen. Die bewusste Auswahl und Anwendung dieser Werkzeuge sichert die Qualität, Nachvollziehbarkeit und letztlich auch den Erfolg der Datenanalysen.