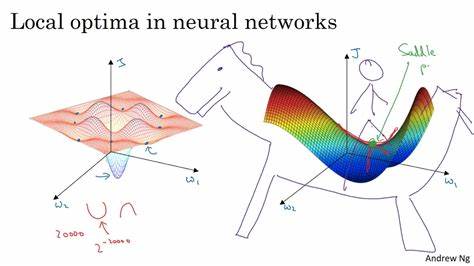
Das N-Queens-Problem ist eines der bekanntesten Herausforderungen im Bereich der Künstlichen Intelligenz und Suchalgorithmen. Die Aufgabe besteht darin, N Damen so auf einem N×N-Schachbrett zu platzieren, dass sich keine zwei Damen gegenseitig angreifen. Dies bedeutet, dass sich keine Dame in derselben Zeile, Spalte oder Diagonale wie eine andere befinden darf. Obwohl das Problem einfach zu formulieren ist, erweist es sich als komplex in der Suche nach einer optimalen Lösung, vor allem bei größeren Brettern. Ein häufiges Hindernis dabei sind lokale Optima, in denen Suchalgorithmen steckenzubleiben drohen, ohne das globale Optimum zu finden.
Der Einsatz von Suchalgorithmen wie Hill Climbing zur Lösung des N-Queens-Problems ist weit verbreitet. Hill Climbing ist ein heuristisches Verfahren, das iterativ die Lösung verbessert, indem es in der unmittelbaren Nachbarschaft nach einem Zustand mit besserem Ergebnis sucht. Dieses Vorgehen wird so lange wiederholt, bis kein besserer Nachbar gefunden wird. Obwohl dieser Ansatz schnell und einfach implementierbar ist, ist er anfällig dafür, in lokalen Optima zu verharren. Das bedeutet, die Suchstrategie erreicht einen Zustand, der zwar besser ist als alle unmittelbaren Nachbarn, aber nicht die beste aller möglichen Lösungen darstellt.
In der klassischen Implementierung des Hill Climbing für das N-Queens-Problem wird das Brett häufig so initialisiert, dass alle Damen auf der linken Seite des Schachbretts stehen. Anschließend wird die Anzahl der Angriffe zwischen den Damen ermittelt, und der Algorithmus versucht, die Damen so zu verschieben, dass diese Angriffe minimiert werden. Ist das Ziel von null Angriffen erreicht, ist eine globale optimale Lösung gefunden und der Prozess endet. Wenn nicht, wird eine Dame zufällig verschoben und der Vorgang wiederholt, was jedoch das Risiko birgt, in einem lokalen Optimum stecken zu bleiben.Die Problematik lokaler Optima entsteht durch die Natur des Suchraums und der Bewertungsfunktion.
Die Funktion, die für jede Brettkonfiguration die Anzahl der Angriffe berechnet, ist das Evaluationselement, das den „Höhenstand“ im Suchprozess beschreibt. Da mehrere Konfigurationen mit null Angriffen das globale Optimum darstellen, existieren auch zahlreiche lokale Minima und Plateaus, die es dem Algorithmus erschweren, das beste Ergebnis zu finden. Die zufälligen Schritte in der Standardimplementierung sind daher oft nicht effizient, um über diese Hürden hinwegzukommen.Um dieses Problem zu adressieren, wurden mehrere innovative Ansätze entwickelt. Eine vielversprechende Strategie ist die Eliminierung der rein zufälligen Schritte und stattdessen ein koordinierteres Verschieben der Damen.
Dabei wird jede Dame systematisch in mögliche Positionen innerhalb ihrer Reihe versetzt, wobei stets die Position ausgewählt wird, die die Angriffszahl minimiert. Sollte die Konfiguration unverändert bleiben, erfolgt eine gezielte zufällige Bewegung, um Impulse für die Verbesserung des Zustandes zu geben. Diese Methode, eine Art von gehirntem Hill Climbing, erhöht signifikant die Chance, eine optimale Lösung zu finden und reduziert das Feststecken in suboptimalen Zuständen.Eine weitere Herangehensweise besteht darin, das Bord zu Beginn und während der Suche zufällig zu variieren, einschließlich der Schrittweite der Dame. Durch die Einführung von Zufälligkeit in der Initialisierung und Dynamik des Algorithmus kann der Suchraum besser erkundet werden.
Dies führt dazu, dass lokale Optima eher umgangen oder durchbrochen werden, da verschiedene Teile des Suchraums systematisch getestet werden. Obwohl dieser Ansatz die Performanz des klassischen Hill Climbing nicht immer übertrifft, zeigt er Potenzial, insbesondere bei komplexeren Instanzen des Problems.Alternativ können andere Algorithmen eingesetzt werden, die von Grund auf besser auf die Problematik lokaler Optima reagieren. Simulated Annealing etwa nutzt eine probabilistische Strategie, bei der auch schlechtere Zustände temporär akzeptiert werden, um aus lokalen Tälern herauszukommen. Genetische Algorithmen imitieren evolutionäre Prozesse, bei denen Populationen von Lösungen durch Kreuzung und Mutation ständig verbessert werden.
Diese Verfahren haben den Nachteil, eventuell höhere Rechenzeit zu benötigen, liefern aber oft robustere Lösungsergebnisse.Im direkten Vergleich haben systematische Ansätze wie das koordinierte Verschieben der Damen besonders bei standardisierten Problemgrößen wie dem 9×9-Brett hervorragende Ergebnisse erzielt. Sie ermöglichen es, in den meisten Fällen eine konfliktfreie Anordnung innerhalb weniger Iterationen zu finden und bieten somit einen attraktiven Kompromiss zwischen Laufzeit und Lösungssicherheit. Zufällige Startkonfigurationen und variierende Schrittweiten zeigen hingegen einen interessanten Effekt auf die Verteilung der Lösungsfindungsdauer, verbessern jedoch selten die Erfolgsquote signifikant.Die Komplexität der einzelnen Ansätze spielt bei der Auswahl des passenden Algorithmus eine wesentliche Rolle.
Funktionen zur Berechnung der Angriffe und zum Auffinden der Position der Damen sind in der Regel konstanter Zeitaufwand, da sie nur einmal pro Zeile agieren. Das Verschieben der Damen in der koordinierten Variante ist hingegen quadratisch bezüglich der Brettgröße, da mehrere mögliche Positionen evaluiert werden müssen. Dadurch steigt die Rechenzeit, aber gleichzeitig verbessert sich auch die Qualität der gefundenen Lösungen.Insgesamt lässt sich festhalten, dass beim N-Queens-Problem die Überwindung lokaler Optima entscheidend für den Erfolg eines Algorithmus ist. Eine reine Zufallsauswahl von Bewegungen führt häufig zu ineffizienten Suchprozessen und Resultaten von minderer Qualität.
Koordinierte, heuristisch fundierte Schritte hingegen erhöhen signifikant die Chance, innerhalb eines angemessenen Zeitrahmens eine globale Optimallösung zu erreichen. Alternative, komplexere Algorithmen bieten zusätzliche Möglichkeiten, sind jedoch nicht immer in der Ausführung effizienter.Die Erfahrung zeigt, dass bei der Wahl des Algorithmus eine Balance zwischen Rechenaufwand und Lösungsqualität angestrebt werden muss. Für praktische Anwendungen, bei denen schnelle Lösungen gefragt sind, ist der koordinierte Hill Climbing-Ansatz besonders empfehlenswert. Gleichzeitig bieten probabilistische und evolutionäre Methoden wertvolle Alternativen für besonders herausfordernde Problemgrößen oder wenn eine höhere Lösungsqualität ohne Zeitdruck angestrebt wird.
Das N-Queens-Problem bleibt somit eine exzellente Lehr- und Forschungsplattform für Suchalgorithmen und Optimierungsstrategien. Die Herausforderungen durch lokale Optima führen zu ständigen Innovationen im Bereich heuristischer Suchverfahren und fördern das Verständnis komplexer Problemräume in der Informatik. Wer sich mit diesem Problem und seinen Lösungsansätzen auseinandersetzt, gewinnt wertvolle Einblicke in die Funktionsweise moderner KI-Methoden und algorithmischer Optimierung.