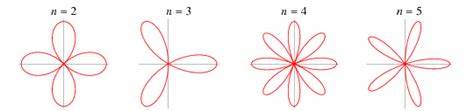
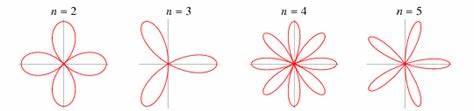
Rosen gehören zu den bekanntesten und beliebtesten Blumen weltweit, bewundert für ihre Schönheit und Anmut. Ein besonders faszinierendes Merkmal sind die filigranen, oft spitz zulaufenden Blütenblätter. Doch wie genau entstehen diese komplexen Formen? Die Antwort darauf liegt in einem ungewöhnlichen mathematischen Phänomen, das Wissenschaftlern erst kürzlich durch physikalische und biologische Untersuchungen klar geworden ist. Die charakteristischen Formen der Rosenblätter sind das Ergebnis einer speziellen Art von geometrischer Rückkopplung, die bisher in der Natur nicht beobachtet wurde. Die Erforschung dieses Mechanismus vereint Disziplinen wie Biophysik, Entwicklungsbiologie und Mathematik und gewährt einen neuen Blick auf den Wachstumsprozess von Pflanzengeweben.
Die Ausgangslage für das Verständnis der Blattform ist die Tatsache, dass Rosenblätter während ihres Wachstums nicht nur einfach flach oder glatt bleiben. Stattdessen entwickeln sie gewölbte Strukturen, eingerollte Kanten und eindrucksvolle Spitzen an ihren Rändern. Diese Formungen dienen wahrscheinlich ästhetischen wie funktionalen Zwecken, wie etwa dem Schutz empfindlicher innerer Gewebe vor Umweltreizen oder der Unterstützung der Blume bei der Fortpflanzung durch Insektenanlockung. Von zentraler Bedeutung bei der Formgebung ist der Wachstumsprozess selbst, der auf sogenannter mechanischer Rückkopplung beruht. Dabei handelt es sich um eine Wechselwirkung zwischen Dehnung und Wachstum: wenn bestimmte Bereiche des Blattes unter Spannung stehen, beeinflusst dies das lokale Wachstum, und umgekehrt wirkt das Wachstum auf die Spannung ein.
Diese Rückkopplung ergibt sich durch die Geometrie des Materials und der daraus entstehenden Kräfte. Die Spitze eines Rosenblatts beispielsweise entsteht dadurch, dass sich die Ränder des Blattes während des Wachstums tendenziell einrollen und verdrehen. Diese Bewegung erzeugt einen mechanischen Druck, der das Wachstum in bestimmten Bereichen beschleunigt oder bremst. Das Resultat ist eine selbstgenügsame Regelung, die letztlich die auffälligen Spitzen und welligen Ränder formt. Die Bedeutung dieses Mechanismus für das Verständnis biologischer Formgebung kann kaum überschätzt werden.
Während bisherige Modelle oft auf genetischen und biochemischen Kontrollsystemen basierten, zeigt sich hier, dass rein physikalische Prinzipien eine zentrale Rolle spielen. Solche geometrischen Feedbackmechanismen könnten in der gesamten Pflanzenwelt weit verbreitet sein, nicht nur bei Rosen. Etwaige Parallelen zu anderen natürlichen Strukturen wie Blättern, Blüten oder sogar der Haut von Tieren laden zu weiteren Untersuchungen ein. Die Entdeckung basiert auf einem interdisziplinären Forschungsansatz, der theoretische Modellierung mit praktischen Experimenten vereint. Wissenschaftler nutzten insbesondere Simulationen mit gummiartigen Kunststoffblättern, die das Wachstum und die Biegeprozesse der Rosenblätter nachahmen.
So konnten sie nachvollziehen, wie durch gezielte Manipulation unterschiedlicher Wachstumsraten an verschiedenen Stellen eine gewölbte Form entstand. Die Modelle belegen, dass das gleichzeitige Wirken von Wachstum und mechanischem Druck die komplexe Spitzenbildung ermöglicht. Darüber hinaus bietet dieser Forschungsansatz auch praktische Anwendungen in der Materialwissenschaft und Ingenieurwesen. Die Erkenntnisse über das Zusammenspiel von Wachstumsprozessen und mechanischem Feedback können als Vorlage dienen, um künstliche Materialien mit selbstregulierenden, dynamischen Oberflächen zu entwickeln. Solche Materialien könnten beispielsweise in der Robotik eingesetzt werden, um flexible, biomimetische Strukturen zu erzeugen, die sich an ihre Umgebung anpassen.
Nicht zuletzt liefert die mathematische Beschreibung des Phänomens neue Impulse für die Theorien der Entwicklung biologischer Formen. Bereits vor über hundert Jahren stellte der berühmte Wissenschaftler D'Arcy Thompson die Frage, wie physikalische Kräfte und Geometrie das Leben formen. Die neueste Forschung an Rosenblättern ist ein moderner Fortschritt dieser Denkweise und zeigt, dass die Komplexität der Natur nicht nur auf Genetik, sondern auch auf physikalischer und mathematischer Ebene verstanden werden muss. Der faszinierende Zusammenhang zwischen Wachstum und Geometrie in Rosenblättern lässt erahnen, wie viele weitere natürliche Formen noch durch ähnliche Mechanismen geformt werden. Es eröffnet sich ein spannendes, interdisziplinäres Forschungsfeld, das Biologen, Physiker und Mathematiker gleichermaßen herausfordert.
Die Mathematik hinter gewellten Kanten und spitzen Enden verbindet Ästhetik mit Wissenschaft und hebt die Natur als das ultimative Meisterwerk der Strukturentwicklung hervor. Zusammenfassend lässt sich festhalten, dass Rosenblätter ihre formale Einzigartigkeit nicht nur durch genetische Bauanleitungen erhalten, sondern auch durch ein bisher unbekanntes mechanisches Feedback, das Wachstum und Spannung miteinander verknüpft. Dieser innovative Blickwinkel erweitert unser Verständnis der morphologischen Vielfalt der Natur und bietet gleichzeitig neue Perspektiven für technische Anwendungen und weiterführende wissenschaftliche Forschung.