Delaunay-Triangulation visualisieren: Ein umfassender Leitfaden zur effizienten Flächenteilung

Analyse des Kryptomarkts Krypto-Betrug und Sicherheit

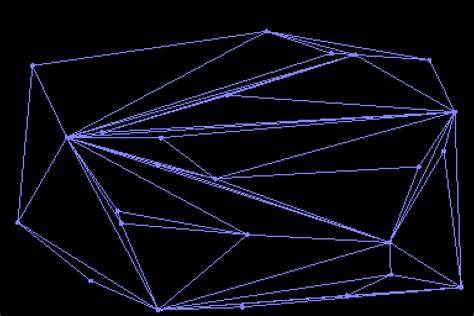
Die Delaunay-Triangulation stellt eine besondere Art der Flächenteilung dar, bei der eine Menge von Punkten im zweidimensionalen Raum so verbunden wird, dass daraus Dreiecksflächen entstehen. Dabei wird ein wichtiges Kriterium eingehalten: Keine Punkte dürfen innerhalb des Umkreises eines der erzeugten Dreiecke liegen. Diese Eigenschaft garantiert, dass die entstandenen Dreiecke möglichst „gleichmäßig“ sind und besonders spitze Winkel vermieden werden. Die Anwendung dieses Prinzips ist weitreichend und reicht von der Computergrafik bis hin zur geodätischen Vermessung. Doch wie funktioniert die Delaunay-Triangulation praktisch, welche Algorithmen stecken dahinter, und warum ist sie oft einem simpleren – aber schlechteren – ersten Ansatz vorzuziehen? Diese Fragen sind zentral, wenn man die Triangulation nicht nur theoretisch versteht, sondern auch effizient visualisieren oder implementieren möchte.

Zunächst ist es wichtig, zu verstehen, warum eine einfache Triangulation oft unzureichend ist. Bei der einfachen Verbindung von Punkten entstehen häufig lange, dünne Dreiecke, die in der Vermessung oder bei der Flächeninterpolation problematisch sind. Diese sogenannten „slivery triangles“ können Verzerrungen verursachen und sind für Berechnungen nur schwer handhabbar. Die Delaunay-Triangulation verfolgt deshalb das Ziel, die minimalen Winkel innerhalb der Dreiecke zu maximieren, was nicht nur optisch ansprechende, sondern auch mathematisch optimale Dreiecke zur Folge hat. Ein sehr einprägsames Merkmal der Delaunay-Triangulation ist ihre Beziehung zum sogenannten Voronoi-Diagramm.

Dieses teilt die Ebene in Regionen ein, die jeweils zu einem bestimmten Punkt gehören – näher an diesem als an jedem anderen. Die Delaunay-Triangulation ist genau der Dualgraph des Voronoi-Diagramms. Das bedeutet, dass man das eine aus dem anderen ableiten kann. Diese duale Beziehung macht die Delaunay-Triangulation zu einem unverzichtbaren Werkzeug beim Umgang mit räumlichen Daten, etwa zur Interpolation von Messwerten an nicht direkt vermessenen Stellen. Ein klassisches praktisches Beispiel stammt aus der Vermessungstechnik: Ein Vermesser misst Höhen an diskreten Punkten eines Geländes.

Er braucht jedoch eine Methode, um die Höhen zwischen diesen Punkten sinnvoll zu bestimmen. Durch die Delaunay-Triangulation dieser Punkte entsteht ein Netz aus Dreiecken, welches auf ein dreidimensionales Höhenmodell übertragen werden kann. So lassen sich Höhenwerte innerhalb von Dreiecken interpolieren, was die Planung und Analyse vereinfacht. Ohne eine gute Triangulation könnten Interpolationen durch fehleranfällige oder verzerrte Dreiecke verfälscht werden. Die Implementierung der Delaunay-Triangulation ist nicht trivial und stellt Programmierer vor einige Herausforderungen.

Ein verbreiteter Ansatz ist der inkrementelle Algorithmus, eingeführt von Guibas und Stolfi im Jahr 1985. Dieser Algorithmus beginnt mit einem sehr großen – theoretisch unendlichen – Dreieck, das alle Punkte umfasst. Dann werden die Punkte Schritt für Schritt eingefügt. Bei jedem Einfügen wird das Dreieck, das den Punkt enthält, in drei neue Dreiecke aufgeteilt. Danach werden die angrenzenden Kanten überprüft, um sicherzustellen, dass alle Kanten die lokale Delaunay-Eigenschaft erfüllen.

Ist dies nicht der Fall, werden Kanten durch sogenannte „Edge-Flips“ getauscht, um das Netz zu optimieren. Dieses Vorgehen garantiert, dass am Ende eine gültige Delaunay-Triangulation entsteht. Eine der mathematisch faszinierenden Aufgaben im Algorithmus ist die Bestimmung, ob ein Punkt innerhalb des Umkreises eines Dreiecks liegt. Das klingt zunächst nach aufwändiger Geometrie: Man müsste den Mittelpunkt des Umkreises berechnen, den Radius bestimmen und anschließend den Abstand des Punktes dazu prüfen. Doch Guibas und Stolfi zeigen eine elegante algebraische Methode.

Statt Umkreis und Mittelpunkt zu berechnen, wird die Lage des Punktes mit Hilfe einer Determinante geprüft, die die Orientierung der Punkte im Raum beschreibt. Dabei werden die ursprünglichen 2D-Punkte durch Einsetzen der Summe aus Quadrat ihrer Koordinaten als dritte Koordinate in 3D verschoben und anschließend die Determinante einer 4x4-Matrix berechnet. Das Vorzeichen der Determinante gibt an, ob der Punkt im Umkreis liegt oder nicht. Diese Methode ist nicht nur elegant, sondern auch effizient, da sie komplexe Berechnungen wie Wurzelziehen vermeidet. Die Datenstruktur zur Repräsentation der Triangulation ist ein weiterer wichtiger Aspekt.

Während einfache Graphenmodelle mit Knoten und Kanten für viele Probleme ausreichend sind, reichen sie hier nicht aus. Man muss zusätzlich die Flächen (Dreiecke) und ihren Zusammenhang modellieren, um Kantenflips und Traversierung effizient zu ermöglichen. Guibas und Stolfi entwickelten die sogenannte Quad-Edge- oder Viertelkanten-Struktur, welche die Graphenstruktur sowie deren Dualgraph gleichzeitig abbildet. Jede logische Kante wird dabei in vier gerichtete Teilkanten zerlegt, welche geschickt miteinander verknüpft werden. Diese Struktur ermöglicht ein einfaches Navigieren in der Triangulation und das Durchführen von Operationen wie dem Verbinden oder Löschen von Kanten, ohne dass Inkonsistenzen im Netz entstehen.

Ein weiterer Knackpunkt bei der Implementierung ist das Auffinden des Dreiecks, in welches ein neuer Punkt eingefügt werden soll. Eine naive Methode stellt das Durchsuchen aller Dreiecke dar, was bei großen Punktmengen ineffizient wäre. Stattdessen nutzen Algorithmen eine lokale Traversierung – von einem Startdreieck aus werden nacheinander benachbarte Dreiecke geprüft, immer in Richtung des gesuchten Punktes. Wird das Dreieck gefunden, in dessen Innerem der Punkt liegt, ist der Einfügevorgang einsatzbereit. Dieses Verfahren arbeitet im Durchschnitt in etwa mit einer Laufzeit von O(√n), was für viele Zwecke ausreichend performant ist.

In interaktiven Anwendungen, etwa bei visueller Bearbeitung, kann zudem die Suche vom zuletzt eingefügten Punkt starten, was die Performance weiter verbessert. Eine Herausforderung bei der Umsetzung ist die Behandlung von Grenzfällen, etwa wenn ein Punkt genau auf einer Kante oder einem Eckpunkt des aktuellen Triangulationsnetzes liegt. In solchen Fällen erzeugt der Algorithmus statt der üblichen drei neuen Dreiecke vier neue. Solche Situationen sind in zufällig generierten Punktmengen selten, müssen aber dennoch korrekt behandelt werden, um die Integrität der Triangulation zu gewährleisten. Das Entfernen oder „Flipping“ der Kanten ist ein weiterer Schlüsselschritt, der mit der Quad-Edge-Struktur elegant umgesetzt werden kann.

Durch Umsortieren der Zeiger der Viertelkanten wird eine Kante so gedreht, dass die lokale Delaunay-Eigenschaft wiederhergestellt wird. Dieser Vorgang sorgt für eine bessere Dreieckverteilung und ist zentral, um die globale Bestimmung der Delaunay-Triangulation aus lokalen Korrekturen herzuleiten. Auch wenn der Algorithmus auf den ersten Blick einfach erscheint, zeigt sich bei der praktischen Umsetzung schnell, wie wichtig die sorgfältige Behandlung von Details ist. Die Frage nach dem großen Ausgangsdreieck, das alle Punkte zumindest anfangs umfassen soll, wird so gelöst, dass einfach ein ausreichend großes Dreieck gewählt wird. Einige Varianten passen dessen Größe dynamisch an, wenn neue Punkte außerhalb des Bereichs auftauchen.

Besondere Aufmerksamkeit erfordert die Behandlung von Punkten, die nahe beieinander oder sogar identisch sind, da sie numerische Instabilitäten auslösen können. Visualisierungen der Delaunay-Triangulation sind besonders hilfreich, um die Funktionsweise und die Fortschritte bei der Triangulation zu verstehen. Moderne Webtechnologien erlauben es, interaktive Darstellungen zu erstellen, bei denen der Nutzer Punkte einfügt, bewegt und das Ergebnis in Echtzeit beobachtet. Solche Visualisierungen zeigen besonders anschaulich, wie sich das Netz beim Einfügen neuer Punkte verändert, wie Kantenflips zur Optimierung beitragen und wie das Eingangsdreieck im Laufe der Zeit immer mehr von der eigentlichen Datenmenge verdrängt wird. Neben der reinen Flächenteilung bieten die Möglichkeiten der Delaunay-Triangulation zahlreiche weitere Anwendungsmöglichkeiten.

Die enge Verbindung zum Voronoi-Diagramm erlaubt, etwa in der Geostatistik oder in der Roboter-Navigation, komplexe räumliche Analysen durchzuführen. Das Generieren von Maschen für Finite-Elemente-Berechnungen in der Ingenieurwissenschaft profitiert ebenfalls von der stabilen Dreiecksverteilung. Die Delaunay-Triangulation ist nicht nur ein akademisches Konzept, sondern überzeugt durch praktische Relevanz und vielseitige Einsatzgebiete. Die Kombination aus mathematischer Eleganz, effizienter Datenstruktur und durchdachtem Algorithmus macht sie zu einer zentralen Technik für alle, die mit räumlichen Punktdaten arbeiten. Durch den fortschrittlichen Ansatz von Guibas und Stolfi ist es heute auch Programmierern möglich, eigene Implementierungen zu entwickeln und anzupassen, was durch intuitive Visualisierungen und offene Ressourcen weiter gefördert wird.

Zusammenfassend ist die erfolgreiche Visualisierung und Implementierung der Delaunay-Triangulation ein spannendes und zugleich komplexes Unterfangen, das fundiertes Wissen in Geometrie, Algebra und Datenstrukturen voraussetzt. Die optimale Triangulation von Punktmengen ermöglicht präzisere und robustere Analysen in zahlreichen wissenschaftlichen und technischen Disziplinen. Wer ihre Mechanismen versteht und beherrscht, steht vor dem Tor zu einer Vielzahl innovativer Anwendungen im Bereich der computergestützten Geometrieverarbeitung.