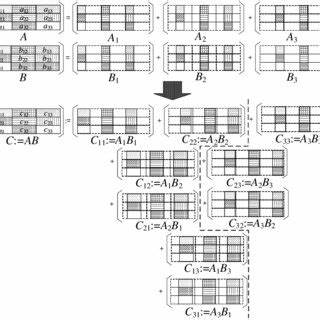
Matrixmultiplikation ist eine der fundamentalsten Operationen im Bereich des wissenschaftlichen Rechnens und der maschinellen Lernalgorithmen. Besonders die General Matrix-Matrix Multiplikation, kurz GEMM genannt, bildet die Basis zahlreicher komplexer Berechnungen in der linearen Algebra und ist integraler Bestandteil vieler High-Performance-Computing-Anwendungen. Traditionsgemäß erfolgt die Matrixmultiplikation mit Gleitkommazahlen direkt auf spezieller Hardware, die Fließkommainstruktionen nativ unterstützt. Dabei kommt es jedoch immer wieder zu Herausforderungen, wenn höhere Präzision oder emulierte Gleitkommaarithmetik auf niedrigstufiger Ganzzahlebene notwendig wird. Genau hier setzt die Ozaki Scheme II an und öffnet vielversprechende Wege für die effiziente und exakte Emulation von Fließkommaberechnungen mittels Integeroperationen.
Die Ozaki Scheme ist eine etablierte Methode, die auf der Zerlegung von Eingabematrizen in mehrere niederrangige Komponenten basiert, um komplexe Gleitkommaprodukte durch präzise, numerisch stabile Teiloperationen zu berechnen. Diese Zerlegung ermöglicht die Vermeidung von Rundungsfehlern, die bei der direkten Gleitkommaoperation auftreten können, und sorgt insgesamt für eine exakte Berechnung des Matrixprodukts in einer Figur von niedrigerer numerischer Präzision. Vorgänger dieser neuen Technik, wie der klassische Ozaki-Algorithmus, haben bereits bewiesen, dass GEMM-basierte Emulationen effizient und skalierbar sind, doch sie stoßen an ihre Grenzen bei der Performance und der Präzision in sehr hohen Genauigkeitsbereichen. Das Ozaki Scheme II, eine innovative Weiterentwicklung dieser Methode, implementiert nun ein geschicktes Verfahren, das sich mathematische Konzepte der modulare Arithmetik und insbesondere den Chinesischen Restsatz zunutze macht. Durch diese Technik kann die Matrixmultiplikation in mehreren modularen Ebenen ausgeführt werden, die jeweils auf integerbasierte Berechnungen zurückgreifen.
Das modulare Verfahren ermöglicht eine exakte Rekonstruktion der ursprünglichen Gleitkommadaten durch Kombination der modularen Teilergebnisse, ohne dass dabei Genauigkeitsverluste entstehen. Dieser Ansatz erlaubt es dem Algorithmus, nur integerbasierte GEMM-Routinen zu verwenden, die auf modernen Hardwareeinheiten, etwa INT8 Tensor Cores von Grafikprozessoren, extrem schnell und energieeffizient ausgeführt werden können. Die Kombination aus Modulares Rechnen und traditioneller GEMM stellt sicher, dass die Emulation sowohl sehr schneller als auch hochpräziser Berechnungen möglich ist. Auf GPUs mit INT8 Tensor Cores konnten mit dieser Methode beeindruckende Leistungswerte von 7,4 bis 9,8 TFLOPS bei FP64 Emulation erreicht werden. Noch eindrucksvoller sind die Zahlen auf Hochleistungs-GPUs wie dem NVIDIA GH200, auf dem die Performance sogar zwischen 56,6 und 80,2 TFLOPS liegt – ein Quantensprung im Vergleich zur nativen FP64-Arithmetik, die diese Karten ebenfalls beherrschen.
Dieses Ergebnis untermauert die enorme Effizienzsteigerung, die durch die Ozaki Scheme II ermöglicht wird. Auch auf CPUs zeigt die Methode signifikante Vorteile, besonders bei der Emulation von Quadruple-Precision-Gleitkommazahlen. Dort konnte eine bis zu 2,3-fache Beschleunigung gegenüber dem klassischen Ozaki-Verfahren erzielt werden. Das macht die Ozaki Scheme II nicht nur zu einem attraktiven Werkzeug für GPU-basiertes High-Performance-Computing, sondern auch für CPU-intensive wissenschaftliche Rechnungen, die extrem hohe Genauigkeit erfordern. Warum ist dieser Fortschritt so bedeutend? Viele Anwendungen, von numerischer Simulation über Finanzmodelle bis hin zur künstlichen Intelligenz, benötigen neben hoher Geschwindigkeit auch außerordentliche Genauigkeit bei numerischen Berechnungen.
Klassische IEEE-754-Gleitkommadarstellungen und deren Hardwareimplementierungen bieten zwar Standardpräzision, speziell im Double-Precision-Bereich, stoßen jedoch bei sehr präzisen oder sehr großen Rechenproblemen an Performance- oder Genauigkeitsgrenzen. Software-Emulationen höherer Genauigkeiten sind zwar möglich, fallen aber in der Regel durch extrem hohen Rechenaufwand und damit unpraktische Laufzeiten negativ auf. Die Ozaki Scheme II tritt hier als Lösung auf, die auf der Gerätespezialisierung und optimierten integerbasierten GEMM-Bibliotheken fußt und zugleich hohe Genauigkeit sicherstellt. Das konzeptuelle Fundament der Ozaki Scheme II kann als eine Mischung aus hochpräzisen Arithmetik-Emulationsverfahren und hardwareorientierter Performance-Optimierung verstanden werden. Die Arbeit verknüpft grundlegende mathematische Techniken mit praktischer Anwendungsorientierung, indem sie die Vorteile der chinesischen Restsatztechnik, eine brillante Methode aus der Zahlentheorie, für die parallele und präzise Matrixmultiplikation nutzt.
Diese Art des modularen Rechnen wurde früher vielfach in der Kryptographie und digitalen Signalverarbeitung geschätzt, findet aber mit Ozaki Scheme II nun einen innovativen Einsatzbereich im wissenschaftlichen Rechnen. Die Implementierung profitiert zudem stark von der Modularität des Programmcodes, indem die einzelnen modularen Berechnungsschritte als unabhängige GEMM-Operationen formuliert werden, die parallelisiert auf modernen Prozessorarchitekturen abgearbeitet werden können. Tensor Cores in modernen GPUs sind speziell für schnelle niedrigpräzise Matrixoperationen optimiert, was diese Hardware ideal für das integerbasierte Vorgehen macht. Damit entsteht eine Verschmelzung von hardwarenahen Optimierungen und mathematischem Know-how, die Performance und Präzision miteinander verbindet – ein Meilenstein für numerische Software. Darüber hinaus ermöglicht die Ozaki Scheme II flexible Kontrolle über Genauigkeit und Rechenaufwand, indem die Anzahl der modularen Matrixmultiplikationen angepasst werden kann.
Dadurch lässt sich ein maßgeschneidertes Optimierungsergebnis erzielen, dass genauer wird, wenn mehr Rechenschritte eingesetzt werden – natürlich auf Kosten von Laufzeit. Dieser Trade-off ist bei spezifischen wissenschaftlichen Anwendungen oder Verfahren im maschinellen Lernen essenziell, um das Optimum aus begrenztem Rechenressourcen herauszuholen. Die Flexibilität des Ansatzes zeigt sich auch in der breiten Einsetzbarkeit der Methode. Während sie zunächst bei 64-Bit-Gleitkommazahlen Anwendung fand, ist eine generalisierte Erweiterung auf noch höhere Präzisionsebenen wie die Quadruple-Precision-Arithmetik durchaus möglich. Gerade im wissenschaftlichen und technischen Computing ist diese Perfektion erforderlich, wenn extrem kleine Fehlertoleranzen bei der Simulation physikalischer Prozesse oder bei hochkomplexen Differentialgleichungen eingehalten werden müssen.
Insgesamt stellt die Ozaki Scheme II eine bahnbrechende Entwicklung im Bereich der hochpräzisen numerischen Linearen Algebra dar. Sie verbindet mathematische Tiefgründigkeit mit praktischer Effizienz und stellt sich so den Anforderungen moderner Hardware und komplexer Anwendungsfälle zugleich. Durch den Einsatz modularer Integerarithmetik über speziell optimierte GEMM-Routinen wird eine hochskalierbare Lösung für anspruchsvolle Matrixmultiplikationen etabliert. Für Forscher, Entwickler und Anwender aus den Bereichen numerische Simulation, Datenwissenschaft, künstliche Intelligenz und High-Performance-Computing eröffnet sich durch diese Methode eine neue Welt an Möglichkeiten. Während traditionelle Fließkommarechner immer weiter ihre Grenzen erfahren, zeigt Ozaki Scheme II, wie innovative Algorithmen in Kombination mit moderner Hardwarearchitektur enormes Potenzial freisetzen können, um sowohl Präzision als auch Leistung auf ein neues Niveau zu heben.