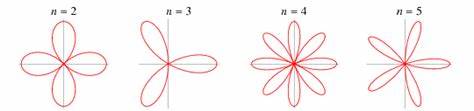
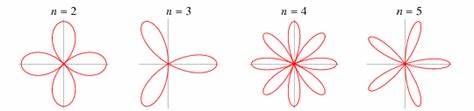
Rosen sind seit jeher ein Symbol für Schönheit und Eleganz. Doch hinter dem anmutigen Aussehen ihrer Blütenblätter verbirgt sich eine komplexe, faszinierende mathematische Welt. Das Wachstum der Rosenblätter folgt nicht nur biologischen Gesetzmäßigkeiten, sondern auch einer ungewöhnlichen Form der Geometrie, die bis vor Kurzem in der Natur unbekannt war. Die Forschung hat gezeigt, dass mechanisches Feedback und spezielle geometrische Prozesse die charakteristischen spitzen Kanten und gewellten Ränder der Blätter erzeugen. Diese Erkenntnisse erweitern unser Verständnis davon, wie sich organische Formen im Laufe der Evolution entwickelt haben und wie komplexe Muster aus einfachen mathematischen Prinzipien entstehen können.
Das Geheimnis der Rosenblattform liegt in einem besonderen geometrischen Effekt, der durch das Wachstum und die Krümmung des Gewebes hervorgerufen wird. Wenn die Rosenblätter wachsen, dehnen sie sich an bestimmten Stellen unterschiedlich stark aus und beginnen sich nach außen zu wölben. Diese Wölbung verändert das mechanische Gleichgewicht der Blattstrukturen und erzeugt eine Rückkopplung, die das Wachstum weiter reguliert. Es entsteht eine Art selbstregulierender Prozess, der bewirkt, dass sich die Ränder der Blätter einrollen und spitze Formen bilden, die bereits für die ästhetische Erscheinung der Blüte verantwortlich sind. Wissenschaftler aus den Bereichen Physik, Mathematik und Biologie haben diese Prozesse mithilfe von theoretischen Modellen, Computersimulationen und experimentellen Nachbildungen mit elastischen Kunststofffolien untersucht.
Durch diese multidisziplinäre Herangehensweise konnten sie nachvollziehen, wie das Wachstum im mikroskopischen Maßstab durch mechanische Kräfte beeinflusst wird und wie sich diese Kräfte im Blattgewebe verteilen. Dabei zeigte sich, dass die Blätter einem speziellen geometrischen Feedbackmechanismus folgen, der bislang in der Natur noch nicht beobachtet wurde. Dieses geometrische Feedback unterscheidet sich von den üblichen Modellen des Pflanzenwachstums, bei denen Form und Struktur überwiegend durch genetische Programmierung und biochemische Signale gesteuert werden. Stattdessen wirkt hier die mechanische Rückkopplung als ein eigenständiger Regulator. Sie sorgt dafür, dass die lokalen Wachstumsraten so angepasst werden, dass das Blatt seine charakteristische Form mit den Rändern, die sich einrollen und spitze Enden bilden, behält.
Dieser Mechanismus ist eine Kombination aus mathematischen Prinzipien der Differentialgeometrie und der Materialwissenschaft. Die Entdeckung dieses seltenen Phänomens hat weitreichende Auswirkungen nicht nur auf die Biologie, sondern auch auf die Materialentwicklung und die technische Gestaltung. Indem Forscher das Verhalten von Rosenblättern besser verstehen, können sie die Prinzipien für neue Arten von flexiblen Materialien und Strukturen übernehmen, die sich unter bestimmten Bedingungen selbst anpassen oder verändern. Solche bioinspirierten Designs können Anwendungen in der Robotik, Architektur oder Medizin finden, wo formverändernde Materialien zunehmend an Bedeutung gewinnen. Die Besonderheit dabei ist, dass die Wölbung und das Einrollen der Blattränder nicht auf simplen Kräften wie Spannen oder Schrumpfen beruhen, sondern auf einem komplexen Zusammenspiel von Wachstumsdynamiken und geometrischer Krümmung.
Es gelang den Forschern, ein präzises mathematisches Modell zu formulieren, das beschreibt, wie genau sich die verschiedenen Kräfte balancieren und in welchem Ausmaß das Gewebe wachsen muss, um die charakteristische Form zu erhalten. Diese Modelle sind nicht nur in der Lage, Rosenblätter nachzubilden, sondern lassen sich auch auf andere natürliche Formen übertragen, bei denen ähnliche Prozesse am Werk sein könnten. Parallel zu den theoretischen Arbeiten wurden praktische Versuche durchgeführt, in denen künstliche elastische Materialien ähnlich wie Pflanzengewebe simuliert wurden. Diese Experimente bestätigten die Hypothese, dass durch gezielte Ansteuerung von Wachstum und mechanischen Kräften bestimmte Figuren und Formen erzeugt werden können. Es eröffnet sich hier ein neues Kapitel der experimentellen Biophysik, in dem man die natürlichen Wachstumsprozesse in kontrollierten Laborumgebungen nachahmt und Stück für Stück entschlüsselt.
Im Zusammenhang mit Rosen ist zudem bemerkenswert, wie die Vielfalt der Blattgestalt variieren kann, je nach Rosenart und Umweltbedingungen. Die mathematischen Prinzipien bleiben dabei erhalten, doch die Ausprägung der Krümmungen und Spitzen variiert. Das unterstreicht, wie flexibel und anpassungsfähig dieses Wachstumssystem ist und wie es evolutionär auf unterschiedliche Bedürfnisse und Lebensräume reagieren kann. Neben der wissenschaftlichen Bedeutung hat die Erkenntnis auch ästhetische und philosophische Dimensionen. Sie macht deutlich, dass Schönheit in der Natur nicht nur zufällig entsteht, sondern durch präzise und komplexe Naturgesetze geprägt wird.
Die Rosenblätter sind so gesehen ein perfektes Beispiel für die Harmonie aus Chaos und Ordnung, aus Wachstum und Feedback, die für das Leben typisch ist. Zusammengefasst lässt sich sagen, dass die ungewöhnliche Mathematik, welche die Form der Rosenblätter bestimmt, ein faszinierendes Beispiel für die Verflechtung von Biologie, Physik und Mathematik darstellt. Durch mechanisches Feedback und geometrische Prinzipien entstehen die markanten, spitzen Kanten und gewellten Ränder, die Rosenblätter so unverwechselbar machen. Dieses Wissen eröffnet neue Perspektiven für Forschung und Technologie und zeigt die Schönheit und Komplexität der Natur in einem ganz neuen Licht.